Лабораторная работа №5. Решение систем линейных уравнений.

Часть 1.

Содержание.

Введение 3.

5.1 Метод Гаусса 3.

5.2 Погрешность решения систем. Нормы матриц. Обусловленность матриц. 5.

5.3 Итерационное уточнение решения линейной системы 8.

Задачи для самостоятельного решения 10.

Задания к лабораторной работе 12.

Приложение 1 13.

Литература 15.

Методы численного решения систем линейных уравнений принято разбивать на две группы, К первой группе относят так называемые точные или прямые методы - это алгоритмы позволяющие получить решение за конечное число арифметических операций. Сюда относится метод Крамера, метод Гаусса и метод прогонки¹. Другую группу состав­ляют приближенные методы, в частности итерационные методы решения систем линейных алгебраических уравнений.

Правило Крамера, при решении задач на ЭВМ не применяется, так как требует большого числа арифметических операций, и, следовательно, дают большую вычислительную погрешность. Метод Гаусса, как правило, используется для решения систем до поряд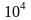ка , а итерационные методы – до порядка .

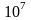Мы уже рассматривали системы уравнений, но эти системы имели низкий порядок и системы задавались точно аналитически. Для систем линейных уравнений эта ситуация не имеет места и поэтому крайне важной становится задача оценки погрешности решения системы, по погрешности поставленной задачи и проблема оптимизации алгоритма, с целью уменьшения вычислительной погрешности.

5.1 Метод Гаусса.

Этот метод наиболее часто применяется для решения систем т.к. он имеет два важных достоинства: выбор ведущего элемента, позволяющий минимизировать погрешность и корректный учет влияния ошибок округления.

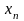В общем случае гауссово исключение состоит из двух этапов: прямого хода и обратного хода. Прямой ход состоит из шагов. На -том шаге кратные -того уравнения вычитаются из оставшихся уравнений с целью исключить -тое неизвестное. Обратный ход состоит в решении последнего уравнения относительно , затем предпоследнего уравнения относительно и т.д., пока из первого уравнения не будет вычислено .

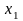Мы всегда будем использовать для системы следующие обозначения:

(1_a)

или в матричном виде:

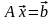, (1_b)

где , , .

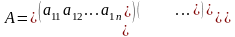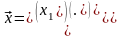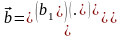Алгоритм в целом может быть компактно записан в матричных обозначениях. Для системы (1) положим:

,

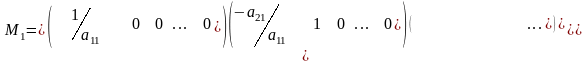и умножая равенство (1) слева на матрицу 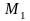получим систему:

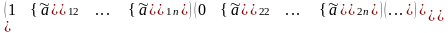(2).

Это преобразование выполнимо, если элемент 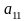, называемый ведущим, не равен нулю.

В этом состоит первый шаг прямого хода метода Гаусса. Второй шаг состоит в умножении равенства (2) на матрицу

.

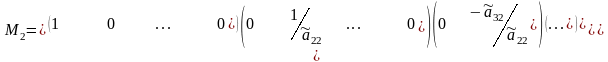Выполняя 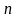шагов прямого хода², получим систему с матрицей верхнего треугольного вида, у которой на главной диагонали стоят единицы

.

Замечание. При выполнении каждого из шагов прямого хода можно уменьшить вычислительную погрешность, для этого в качестве ведущего элемента следует выбирать максимальный по модулю элемент разрешающего столбца, находящийся ниже элемента стоящего на главной диагонали³. Говоря другими словами, при каждом шаге на диагональ переставляется уравнение с максимальным по модулю коэффициентом при исключаемой неизвестной.

Далее выполняя обратный ход, получим решение системы. Т.е. для реализации этого алгоритма на ЭВМ достаточно иметь процедуры: перемножения матриц, перестановки строк матрицы и построения матрицы. Для законченности алгоритма необходимо уметь подсчитывать погрешность решения системы, чем мы и займемся в следующем параграфе.