5.2 Погрешность решения системы. Нормы матриц. Обусловленность систем.

Поскольку мы договорились оценивать погрешность решения как расстояние между точным и приближенным решениями системы, то нам потребуется определить норму матрицы, и ее определим, согла­сованно с определением нормы вектора:

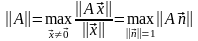(1).

Отсюда непосредственно следует, что (1) удовлетворяет аксиомам нормы

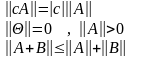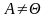, для ⁴.

Таким образом, множество 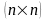матриц может быть интерпретировано как нормированное векторное пространство размерности 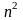. Также из (1) следует, что

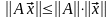. (2)

Более того, неравенство (2) является “неулучшаемым”, в том смысле, что для каждой матрицы 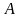найдется вектор 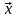, такой, что

.

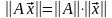Квадратная матрица задает линейное преобразование каждого вектора в вектор 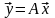, можно считать, что формула (1) определяет 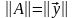как наибольшую длину образа вектора единичной сферы при преобразовании .

Если выбрать евклидову норму в качестве нормы вектора, то можно интерпретировать норму матрицы следующим образом: При выполнении линейного преобразования единичная сфера деформируется в эллипсоид⁵, тогда норма матрицы 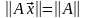, представляет собой длину максимальной полуоси эллипсоида. Или, что норма диагональной матрицы равна максимальному по модулю элементу диагонали. Также следует, что умножение матрицы на любую ортогональную матрицу не изменяет ее нормы.

Мы интерпретировали только одну из возможных норм векторов. Две другие, обычно используемые в численном анализе нормы таковы:

.

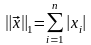
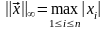Эти две нормы порождают соответствующие матричные нормы:

.

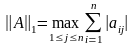
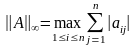Предлагается, в качестве упражнения, интерпретировать их в двух и трехмерном пространствах.

Для расчета погрешности решений системы будем вначале полагать, что матрица системы задана точно, а вектор правых частей приближенно 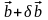и выясним, как велико может быть 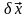. Имеем следующую цепочку соотношений:

,

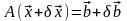
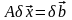
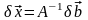
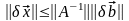так как 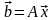, то 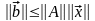. Перемножая, обе части последних неравенств, имеем:

.

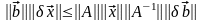Предполагая, что 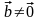, получим

.

Для любой невырожденной матрицы определим сейчас ее число обусловленности, обозначаемое 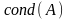, как произведение 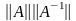⁶ и предыдущая формула перепишется в виде

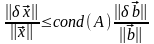. (3)

Теперь это соотношение можно интерпретировать следующим образом: есть мера относительной неопределенности в задании вектора 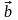. Аналогично 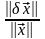можно интерпретировать как меру относительной неопределенности вектора решения системы. Поскольку неравенство является не улучшаемым, то правая часть (3) есть предельная относительная погрешность.

До сих пор мы предполагали, что матрица A известна точно, вектор правых частей имеет неопределенность. Предположим теперь, что матрица A известна приближенно

,

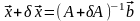тогда 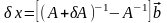, после этого, воспользовавшись тождеством

,

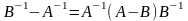найдем 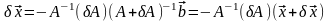. Переходя в этой формуле к нормам: получаем

.

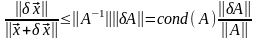Объединяя полученные результаты, мы будем иметь соотношение для погрешности решения системы вследствие представления данных в арифметике с плавающей запятой⁷

,

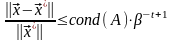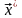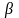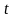где -вычисленное решение, -основание системы счисления, -длина разрядной сетки мантиссы. Следует заметить, что этот вывод справедлив, если мы пренебрегаем погрешностью возникающей при выполнении арифметических операций. Это предположение оправдано тем обстоятельством, что если эта погрешность и возникает, то она минимизируется выбором ведущего элемента при прямом ходе метода Гаусса.

Все результаты рассмотрения можно сформулировать в окончательном виде: Предположим, что все элементы и точно представляются в арифметике с плавающей запятой, и пусть вектор , получен на выходе подпрограммы решения системы линейных уравнений. Предположим также, что точная вырожденность матрицы, если она имеет место, не была обнаружена, и что не было ни машинных нулей, ни переполнений. Тогда имеют место следующие неравенства:

,

.

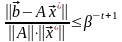Здесь - основание системы счисления арифметики, - длина разрядной сетки мантиссы.

Второе неравенство утверждает, что, как правило, можно рассчитывать на то, что относительная невязка будет иметь величину, сравнимую с ошибкой округления, независимо от того, насколько плохо обусловлена матрица.