
- •Лабораторная работа №5. Решение систем линейных уравнений.
- •Часть 1.
- •Содержание.
- •5.1 Метод Гаусса.
- •5.2 Погрешность решения системы. Нормы матриц. Обусловленность систем.
- •5.3 Итерационное уточнение решения линейной системы.
- •Задачи для самостоятельного решения.
- •Задания к лабораторной работе.
- •Приложение 1. Вычисление нормы матрицы согласованной с евклидовой нормой вектора.
- •Литература.
Задания к лабораторной работе.
Решить системы уравнений, с максимально возможной точностью, для данных одинарной точности :
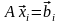 .
.
Основная
матрица системы порядка
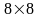 одинакова для всех вариантов и ее
элементы равны
одинакова для всех вариантов и ее
элементы равны
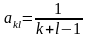 .
.
Вектор
правых частей, в каждом варианте
получается расчетом значений функции
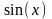 ,
для
,
для
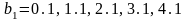 ,
с шагом
,
с шагом
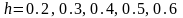 .
.
Порядок выполнения работы:
Составить и отладить процедуры, реализующие прямой ход метода Гаусса.
На основании полученных процедур составить подпрограмму расчета матрицы, приводящей матрицу к верхнему треугольному виду.
Составить и отладить подпрограмму расчета числа обусловленности матрицы и провести расчет.
Выполнить обратный ход метода Гаусса.
Провести расчет невязки и уточнить полученное решение.
Приложение 1. Вычисление нормы матрицы согласованной с евклидовой нормой вектора.
Мы
уже отмечали, что величина нормы матрицы
и число обусловленности зависят от
выбора типа нормы. Если для норм
и
 их расчет производится по явным формулам
достаточно просто, то вычисление числа
обусловленности требует знания обратной
матрицы9,
что, вообще говоря, эквивалентно решению
системы и поэтому простота расчета
указанных норм не гарантирует простоту
расчета числа обусловленности матрицы.
их расчет производится по явным формулам
достаточно просто, то вычисление числа
обусловленности требует знания обратной
матрицы9,
что, вообще говоря, эквивалентно решению
системы и поэтому простота расчета
указанных норм не гарантирует простоту
расчета числа обусловленности матрицы.
Для
подсчета евклидовой нормы матрицы
,
с отличным то нуля определителем введем
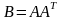 ,
заметим, что данная матрица является
симметричной. Более того, для любого
вектора
,
заметим, что данная матрица является
симметричной. Более того, для любого
вектора
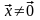
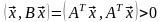 ,
,
следовательно,
матрица
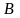 положительно определена. Это означает,
что все ее
собственных значений положительны, так
что мы можем их обозначить через
положительно определена. Это означает,
что все ее
собственных значений положительны, так
что мы можем их обозначить через
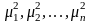 ,
причем можно положить
,
причем можно положить
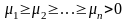 ,
,
эти
числа называют сингулярными
числами
матрицы
.
Из теории вещественных симметрических
матриц следует, что можно найти
ортогональную матрицу
 ,
такую, что
,
такую, что
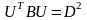 ,
,
где
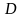 -
диагональная матрица с элементами
-
диагональная матрица с элементами
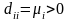 .
Теперь определим матрицу
.
Теперь определим матрицу
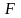 как
как
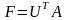 .
.
Тогда
 ,
так что матрица
,
так что матрица
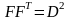 является диагональной. Более того,
последнее равенство показывает, что
различные строки матрицы
ортогональны друг другу
является диагональной. Более того,
последнее равенство показывает, что
различные строки матрицы
ортогональны друг другу
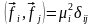 .
Построим ортонормированную систему
вектор-строк
.
Построим ортонормированную систему
вектор-строк
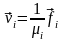 ,
для
,
для
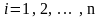 .
Пусть
.
Пусть
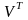 -
матрица строками которой являются
вектора
-
матрица строками которой являются
вектора
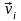
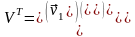 ,
,
тогда
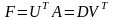 и следовательно
и следовательно
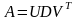 .
Тем самым доказана:
.
Тем самым доказана:
Теорема.
Для любой невырожденной матрицы
существуют две вещественные ортогональные
матрицы
и
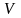 ,
такие, что
,
такие, что
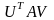 диагональная матрица
.
Более того, можно выбрать
и
так, чтобы диагональные элементы
имели вид:
диагональная матрица
.
Более того, можно выбрать
и
так, чтобы диагональные элементы
имели вид:
.
Из
этой теоремы следует, что
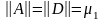 и норма
и норма
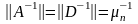 ,
следовательно
,
следовательно
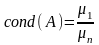 .
Т.е., для вычисления числа обусловленности
матрицы достаточно найти максимальное
.
Т.е., для вычисления числа обусловленности
матрицы достаточно найти максимальное
 и минимальное
и минимальное
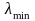 собственные значения матрицы
собственные значения матрицы
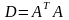 и окончательно
и окончательно
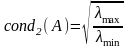 .
Укажем итерационный алгоритм, принадлежащий
Л. А. Люстернику, который позволяет найти
наибольшее собственное значение
симметричной положительно определенной
матрицы
.
Рассмотрим итерационный процесс
.
Укажем итерационный алгоритм, принадлежащий
Л. А. Люстернику, который позволяет найти
наибольшее собственное значение
симметричной положительно определенной
матрицы
.
Рассмотрим итерационный процесс
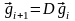 ,
причем
,
причем
 -
произвольный ненулевой вектор. Покажем,
что
-
произвольный ненулевой вектор. Покажем,
что
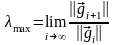 .
.
Для
этого представим
в виде разложения по полной системе
собственных векторов
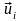 матрицы
,
матрицы
,
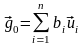 .
.
После -той итерации будем иметь:
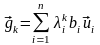 .
.
Перепишем последнее равенство в виде:
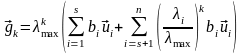 ,
,
где в первой сумме выписаны собственные векторы, принадлежащие собственному значению . На основании этого равенства имеем
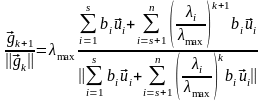 .
.
Переходя
к пределу, при
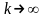 получим:
получим:
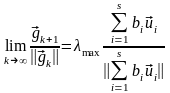 .
.
Переходя в этом соотношении к норме, получим искомый результат:
. (1)
Минимальное
собственное значение
матрицы
можно получить, если найти
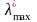 максимальное собственное значение
матрицы
максимальное собственное значение
матрицы
 ,
которое связано с
соотношением
,
которое связано с
соотношением
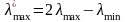 .
.
Замечание. При реализации итерационного процесса основанного на формуле (1), для сокращения числа арифметических операций дробь в правой части формулы можно вычислять не для всех значений , а с некоторым разумным интервалом, например через каждые десять шагов итерации.
