
- •1.Целые и рациональные числа.
- •2.Действительные числа.
- •3. Десятичные приближения действительного числа по недостатку и по избытку. Арифметические действия с действительными числами.
- •4.Числовая прямая.
- •5.Приближенные значения величин. Погрешность приближения.
- •6.Оценка погрешности.
- •7.Сложение и вычитание приближенных величин.
- •8.Умножение и деление приближенных величин.
- •9.Относительная погрешность.
2.Действительные числа.
Все числа представимые бесконечными десятичными дробями , образуют множество действительных чисел. Познакомимся с одним из способов построения теории действительных чисел в общих чертах.
Принимают:
а) каждому действительному числу соответствует (в качестве его записи)
бесконечная десятичная дробь:
соответствует (в качестве его записи)
бесконечная десятичная дробь:
 ;
;
б) каждая бесконечная десятичная дробь является записью действительного числа.
Но при этом естественно считать десятичную дробь, заканчивающуюся бесконечной последовательностью девяток, лишь второй записью числа, выражающегося десятичной дробью, заканчивающейся бесконечной последовательностью нулей:
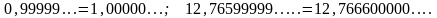
Такое соглашение поясним примером:
 .
Только исключив из рассмотрения
десятичные дроби с девяткой в периоде,
получаем взаимно однозначное соответствие
между множеством действительных чисел
и множеством бесконечных десятичных
дробей.
.
Только исключив из рассмотрения
десятичные дроби с девяткой в периоде,
получаем взаимно однозначное соответствие
между множеством действительных чисел
и множеством бесконечных десятичных
дробей.
Вводят правило сравнения двух действительных чисел х и у .
Если целая часть числа х меньше целой части числа у, то сам о число х меньше числа у. Для сравнения двух чисел, целые части которых равны, приходится обращаться к их дробным частям.
Например,
 , так как у этих чисел равны целые части
и три первых десятичных знака после
запятой, а четвертый знак после запятой
у числа в левой части меньше:
, так как у этих чисел равны целые части
и три первых десятичных знака после
запятой, а четвертый знак после запятой
у числа в левой части меньше:
 .
.
Правило сравнения действительных
чисел, записанных в виде бесконечных
десятичных дробей, можно сформулировать
так:
 .
.
Принимают определения арифметических действий ( операций) над действительными числами: сложения и умножения, вычитания и деления. ( см. следующий пункт)
Показывают, что неравенства и арифметические операции, определенные в множестве действительных чисел, сохраняют основные свойства, присущие им в множестве рациональных чисел.
Модуль действительного числа определяется так же ,как и модуль рационального числа:
 .
.
Например, если
 ,
то
,
то .
.
3. Десятичные приближения действительного числа по недостатку и по избытку. Арифметические действия с действительными числами.
Для числа
 число
число называют десятичным приближением по
недостатку с точностью до
называют десятичным приближением по
недостатку с точностью до
 ( или с точностью до n
знаков), а число
( или с точностью до n
знаков), а число десятичным приближением по избытку
с точностью до
.
Из правил сравнения действительных
чисел следует, что
десятичным приближением по избытку
с точностью до
.
Из правил сравнения действительных
чисел следует, что
 .
.
Пример 1. Запишем десятичные приближения
числа
 по недостатку и избытку с точностью до
1, до 0,1, до 0,01, ..., до 0,00001:
по недостатку и избытку с точностью до
1, до 0,1, до 0,01, ..., до 0,00001:

С помощью десятичных приближений определяются операции сложения и умножения действительных чисел. Эти определения даются, исходя из следующих соображений.
Если
 и
и
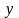 рациональные числа, то сумма
рациональные числа, то сумма
 уже определена, причем для любого n
выполнены неравенства
уже определена, причем для любого n
выполнены неравенства
 .
.
Это свойство суммы должно быть сохранено
и для произвольных действительных чисел
(хотя бы для того, чтобы их сумму можно
было находить приближенно). В курсах
математического анализа доказывается,
что для любой пары действительных чисел
и
существует единственное число такое, что при любом
такое, что при любом
 выполняется
неравенство
выполняется
неравенство

Это число
называется суммой чисел
и
(обозначается
 ).
).
Пример 2. Найдем первые четыре десятичных
знака суммы
,
где
 .
.
Здесь многоточием отмечены следующие десятичные знаки, которые для решения не нужны. Для заданных чисел выпишем десятичные приближения с точностью до пяти знаков. Тогда
 .
.
Вы видите, что слева и справа совпадают
четыре десятичных знака. Следовательно
 .
.
Ответ: .
Произведение неотрицательных действительных чисел определяется аналогично. Можно доказать, что для любой пары неотрицательных действительных чисел и существует единственное число действительное число такое, что при любом выполняется неравенство
 .
.
Это число
называется произведением чисел
и
(обозначается
 ).
).
Для действительных чисел разных знаков,
воспользовавшись тем, что произведение
неотрицательных чисел и
и
 уже определено, полагают:
уже определено, полагают:
 ; в остальных случаях
; в остальных случаях
 .
.
Вычитание определяется, как действие обратное сложению, деление – как действие, обратное умножению.
Пользуясь определениями арифметических операций, получаем основные свойства модуля :
 ;
;
 ;
;
 .
.
