
Міністерство освіти і науки україни
ОДЕСЬКИЙ НАЦІОНАЛЬНИЙ ПОЛІТЕХНІЧНИЙ УНІВЕРСИТЕТ
Вища математика
Методичні вказівки до розв’язання завдань за темою
Диференціальні рівняння
для студентів денної форми навчання
інституту електромеханіки та енергоменеджмента
Затверджено
на засіданні кафедри
вищої математики № 2
протокол №8 від 23.01.04.
Одеса 2004
Вища математика. Методичні вказівки до розв’язання контрольних завдань з темою „Диференціальні рівняння” для студентів денної форми навчання інституту електромеханіки та енергоменеджмента / Укл. Т.О.Комлєва, Л.І.Плотнікова, А.В.Усов, М.О.Юрченко
Зразок розв’язання типових задач
Задача 1. Знайти загальний розвязок диференціального рівняння та побудувати інтегральну криву, що проходить через дану точку.
![]() M
( /4
, 0 ).
M
( /4
, 0 ).
Розвязання.
Проiнтегруємо рівняння i одержимо
загальний розвязок
:
![]() .
Довільну сталу С
визначимо з початкової умови y(
/4
) = 0
C
= 0. Тоді для інтегральної кривої, що
проходить через точку М, матимемо:
.
Довільну сталу С
визначимо з початкової умови y(
/4
) = 0
C
= 0. Тоді для інтегральної кривої, що
проходить через точку М, матимемо:
![]() y
= sin x – cos x, або
y
= sin x – cos x, або
![]() .
.
Побудуємо
її ( рис. 1 ) за схемою:
![]()
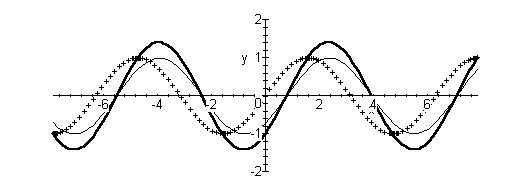
Рис. 1.
(
+ + +
![]() ;
____
;
____
![]() ______
______
![]()
 ).
).
Задача 2. Встановити аргументовано тип рівняння та вказати метод його розв’язку. Знайти загальний або частинний розв’язок рівняння.
1).
![]()
Розв’язання. Запишемо дане рівняння у вигляді:
![]() -
-
це рівняння з відокремлюваними змінними типу
![]() .
.
Отже,
якщо
![]() ,
то дістанемо:
,
то дістанемо:
![]()
Інтегрування
дає :
![]()
або
![]() - загальний інтеграл даного рівняння.
- загальний інтеграл даного рівняння.
2).
![]()
Розв’язання. Розв’яжемо рівняння відносно похідної:
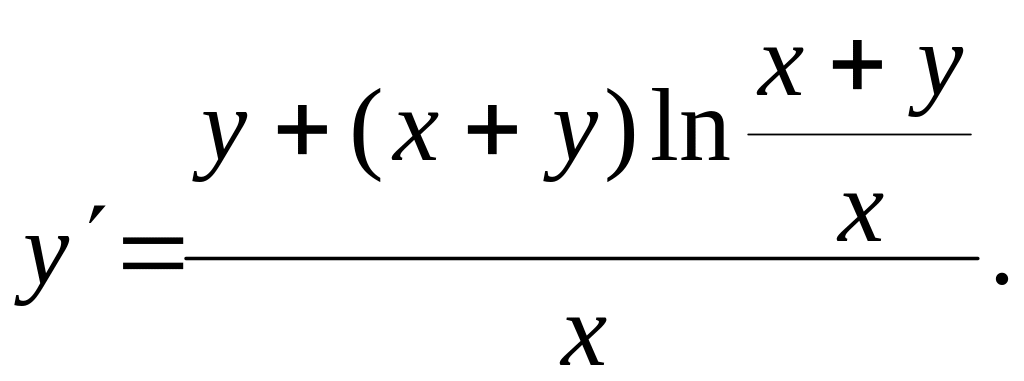
Легко бачити, що права частина є однорідною функцією виміру 0. Дійсно,

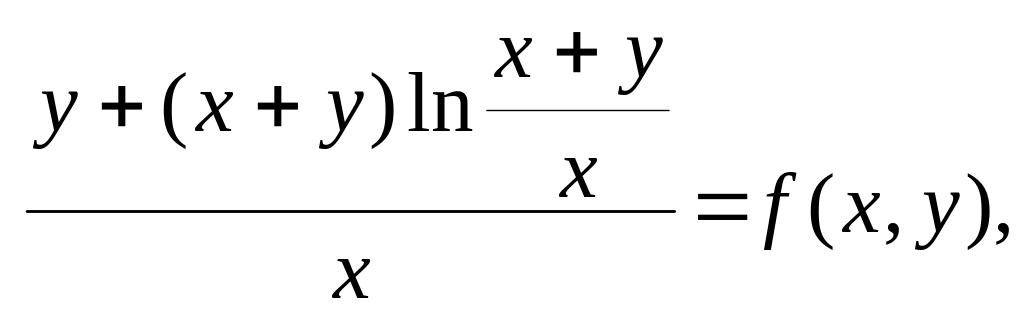
і задане рівняння можемо записати у вигляді:
![]()
Отже,
це однорідне рівняння, яке заміною
![]() зводиться до рівняння з відокремлюваними
змінними:
зводиться до рівняння з відокремлюваними
змінними:
![]()
![]()
![]()
![]() Після
потенціювання маємо:
Після
потенціювання маємо:
![]() Отже,
Отже,
![]() -
загальний розв’язок рівняння.
-
загальний розв’язок рівняння.
3).
![]()
Розв’язання.
Задане рівняння є лінійним відносно
функції
![]()
![]() .
Продемонструємо на прикладі цього
рівняння методи Лагранжа і Бернуллі.
.
Продемонструємо на прикладі цього
рівняння методи Лагранжа і Бернуллі.
Метод Лагранжа дає такий ланцюжок перетворень:
![]()

Отже, загальний розв’язок заданого рівняння має вигляд:
![]() де
де
![]() довільна
стала.
довільна
стала.
Метод Бернуллі приводить до інших перетворень:
![]()
![]() Звідки
Звідки
![]()
Остаточно:
![]()
4).
![]()
Розв’язання.
Задане рівняння є лінійним відносно
функції
![]() Дійсно:
Дійсно:
![]() Крім
методів Лагранжа і Бернуллі часто
використовують метод Ейлера ( інтегрального
множника ), який приводить до розв’язку
цього рівняння у вигляді ( рекомендуємо
цю формулу вивчити на пам’ять ):
Крім
методів Лагранжа і Бернуллі часто
використовують метод Ейлера ( інтегрального
множника ), який приводить до розв’язку
цього рівняння у вигляді ( рекомендуємо
цю формулу вивчити на пам’ять ):
![]()
В результаті одержимо:
![]()
Остаточно
маємо:
![]() З
початкової умови знайдемо сталу С:
З
початкової умови знайдемо сталу С:![]() Отже, інтегральна крива, що проходить
через точку (1; 0) має рівняння:
Отже, інтегральна крива, що проходить
через точку (1; 0) має рівняння:
![]()
5).
![]()
Розв’язання. Перепишемо задане рівняння у вигляді:
![]() -
рівняння Бернуллі (
-
рівняння Бернуллі (
![]()
![]() ,
де
,
де
![]()
![]() ), розв’язок якого
), розв’язок якого
можна
одержати методом Бернуллі
![]() або звести до лінійного рівняння заміною
або звести до лінійного рівняння заміною
![]()
За методом Бернуллі маємо:
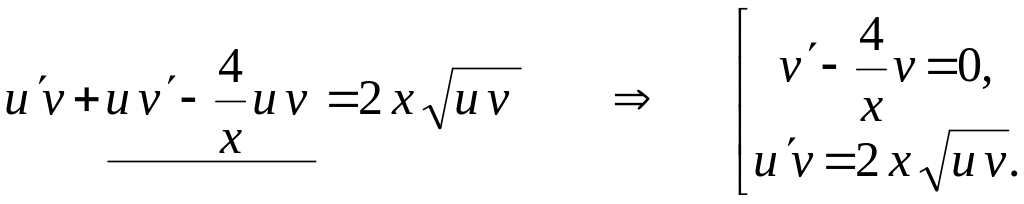
Звідки
![]()
![]() Тому
загальний розв’язок рівняння:
Тому
загальний розв’язок рівняння:
![]()
Продемонструємо метод зведення рівняння Бернуллі до лінійного, переписавши його у вигляді:
![]() Поклавши
Поклавши
![]() маємо
маємо
![]()
За
методом Ейлера розв’язок лінійного
рівняння
![]() має вигляд:
має вигляд:
![]()
Остаточно
![]()
Зауважимо,
що
![]() також є розв’язком цього рівняння.
також є розв’язком цього рівняння.
6).
![]()
Розв’язання. Запишемо дане рівняння у симетричній формі:
![]()
![]()
(
![]()
де
![]() =
=![]() ,
,
![]()
![]() ).
).
Оскільки
![]() тобто
тобто
![]()
то
дане рівняння є рівнянням у повних
диференціалах. Його розв’язок має
вигляд
![]() ,
де С – довільна стала, а
,
де С – довільна стала, а
![]() -
функція, для якої
-
функція, для якої

Інтегруючи перше рівняння системи по x, одержимо:
![]() де
де
![]() - довільна функція від y.
- довільна функція від y.
Підставимо
![]() у друге рівняння системи:
у друге рівняння системи:
![]()
![]() звідки
звідки
![]()
![]() Отже,
Отже,
![]() і
і
![]() -
загальний інтеграл заданого рівняння.
-
загальний інтеграл заданого рівняння.
Зауважимо,
що
![]()
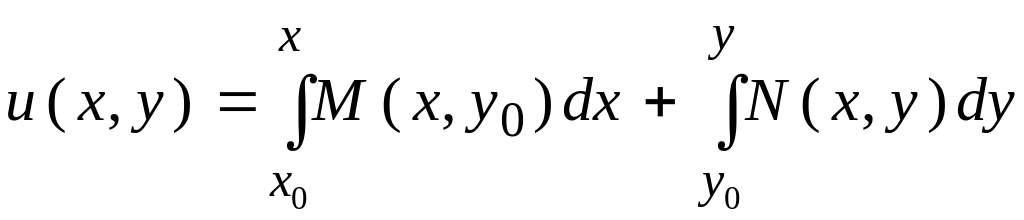 ,
де
,
де
![]() -
фіксована довільна точка із області, в
якій виконуються умови існування та
єдиності розв’язків рівняння.
-
фіксована довільна точка із області, в
якій виконуються умови існування та
єдиності розв’язків рівняння.
Задача 3. а). Описати тип диференціального рівняння, вказати метод його розв’язку.
б). Знайти загальний або частинний розв’язок диференціального рівняння.
1).
![]()
рівняння
вигляду
![]() яке можна розв’язати відносно похідної
яке можна розв’язати відносно похідної
![]() і послідовно двічі проінтегрувати.
Отже маємо:
і послідовно двічі проінтегрувати.
Отже маємо:
![]()
![]()
![]()
2).
![]()
Розв’язання.
Оскільки задане рівняння явно не містить
шуканої функції, то його порядок можна
знизити, застосувавши підстановку
![]() ,
де
,
де
![]() Тоді
Тоді
![]() Отже,
маємо:
Отже,
маємо:
![]()
однорідне
рівняння першого порядку, яке заміною
![]()
зводиться
до рівняння з відокремлюваними
змінними. Маємо:![]()
![]()
![]()
Розв’яжемо
останнє рівняння відносно p:

![]() загальний
розв’язок заданого рівняння.
загальний
розв’язок заданого рівняння.
3).
![]()
Розв’язання.
Задане рівняння типу
![]()
![]()
тобто
воно не містить явно незалежної змінної
![]() ,
а в даному випадку відсутня і
,
а в даному випадку відсутня і
![]() (що не суттєво). Заміна
(що не суттєво). Заміна
![]() ,
де
,
де
![]() - нова функція аргументу
- нова функція аргументу
![]() ,
знижує порядок рівняння на одиницю.
При цьому враховуємо, що
,
знижує порядок рівняння на одиницю.
При цьому враховуємо, що
![]() тоді
тоді
![]()
![]() або
або
![]()
Використовуючи
початкові умови
![]() ,
тобто
,
тобто
![]() ,
знаходимо
,
знаходимо
![]() Отже,
Отже,
![]()
Оскільки
![]() то в околі
то в околі
![]() функція
функція
![]() зростає. Отож,
зростає. Отож,
![]() Розділимо змінні:
Розділимо змінні:
![]()
З
початкових умов маємо:
![]() Отже,
Отже,
![]() -
розв’язок задачі Коші.
-
розв’язок задачі Коші.
Задача
4.
Задана система функцій
![]() .
.
а). Перевірити її на лінійну незалежність.
б).
Побудувати однорідне диференціальне
рівняння, фундаментальна система
розв`язків якого – функції
![]()
в). Розв`язати одержане рівняння.
Розв`язання. Оскільки відношення цих функцій на множині їх визначення тотожньо не дорівнює сталій величині:
![]()
![]() ,
,
то вони лінійно незалежні і утворюють фундаментальну систему розв’язків для лінійного однорідного рівняння, яке можна подати у вигляді:
![]() ,
,
де ліва частина - визначник Вронського для системи функцій у(х), у1(х), у2(х). Після розкладу за першим стовпцем матимемо:
![]()
отже,
![]() - шукане лінійне однорідне рівняння.
- шукане лінійне однорідне рівняння.
Загальний розв’язок цього рівняння можна записати у вигляді:
![]()
![]() ,
де А,
В, C1=А,
C2=А+В
– довільні сталі.
,
де А,
В, C1=А,
C2=А+В
– довільні сталі.
Цей
же розв’язок можна одержати згідно
методу розв’язку лінійного однорідного
рівняння зі сталими коефіцієнтами.
Запишемо характеристичне рівняння
![]() ,
його корені 1=3,
,
його корені 1=3,
2
=
-3. Звідки фундаментальна система
розв’язків
![]() ,
і загальний розв’язок:
,
і загальний розв’язок:
![]()
Задача 5. а). Знайти частинний розв’язок лінійного рівняння
![]()
![]() ,
,
![]() .
.
Розв`язання. а) Розв’яжемо лінійне диференціальне рівняння другого порядку з постійними коефіцієнтами за методом
Ейлера
, тобто розв’язок будемо шукати у вигляді
![]() .
Маємо характеристичне рівняння: 2
+
4 = 0; його корені 1,2
=
2j.
Отже, загальний розв’язок цього рівняння
в дійсній формі має вигляд:
.
Маємо характеристичне рівняння: 2
+
4 = 0; його корені 1,2
=
2j.
Отже, загальний розв’язок цього рівняння
в дійсній формі має вигляд:
![]() .
.
Використаємо
початкові умови для знаходження C1
і C2.
Оскільки
![]() ,
маємо: C1=2,
C2=3.
,
маємо: C1=2,
C2=3.
Отже,
![]() – шуканий частинний розв’язок задачі
Коші.
– шуканий частинний розв’язок задачі
Коші.
б) Записати загальний вигляд з невизначеними коефіцієнтами розв’язку лінійного рівняння
![]() .
.
Розв`язання.
Загальний розв’язок ЛНДР будемо шукати
у вигляді
![]() де
де
![]() -
загальний розв’язок відповідного
однорідного рівняння,
-
загальний розв’язок відповідного
однорідного рівняння,
![]() який-небудь
частинний розв’язок неоднорідного
рівняння. Маємо:
який-небудь
частинний розв’язок неоднорідного
рівняння. Маємо:
![]() ,
С1,
С2
–
довільні сталі.
,
С1,
С2
–
довільні сталі.
Права
частина заданого рівняння має спеціальний
вигляд:
![]()
![]() ,
,
де
![]() .
Числа
.
Числа
![]() - корені характеристичного рівняння,
кожний кратності s=1. Тоді частинний
розв’язок згідно методу
невизначених коефіцієнтів має
вигляд:
- корені характеристичного рівняння,
кожний кратності s=1. Тоді частинний
розв’язок згідно методу
невизначених коефіцієнтів має
вигляд:
![]() .
.
Тоді
![]() .
.
в). Розв’язати задачу Коші
![]()
Розв`язання. Спочатку знайдемо коефіцієнти в частинному розв’язку:

![]()
Отже, загальним розв’язком рівняння є функція:
![]() .
.
Знайдемо
похідну
![]() і використаємо початкові умови для
визначення
і використаємо початкові умови для
визначення
![]() .
.
![]() .
.![]()
Отже,
![]() – шуканий розв’язок задачі Коші.
– шуканий розв’язок задачі Коші.
Задача
6.
Знайти
частинний розв’язок лінійного рівняння:
a).
![]()
![]() ,
,
![]() .
.
Розв`язання. Складемо характеристичне рівняння:
![]() його
корені 1,2
=
5.
його
корені 1,2
=
5.
Отже, S(t)=(C1+C2 t) e 5 t – загальний розв’язок лінійного однорідного рівняння другого порядку з постійними коефіцієнтами.
З початкових умов визначимо сталі C1 і C2 :
![]() ,
звідки маємо :
,
звідки маємо :
![]()
Отже,
![]() – розв’язок задачі Коші.
– розв’язок задачі Коші.
б).
![]()
![]() ,
.
,
.
Розв’язання.
Загальний розв’язок лінійного
неоднорідного диференціального рівняння
другого порядку з постійними коефіцієнтами
шукатимемо у вигляді:
![]() де
де
![]() -
загальний розв’язок відповідного
однорідного рівняння
-
загальний розв’язок відповідного
однорідного рівняння
![]() .
.
Частинний
розв’язок
![]() неоднорідного рівняння будемо шукати
у вигляді
неоднорідного рівняння будемо шукати
у вигляді
![]() ,
користуючись методом невизначених
коефіцієнтів, оскільки права частина
,
користуючись методом невизначених
коефіцієнтів, оскільки права частина
![]() має
спеціальний вигляд, причому
має
спеціальний вигляд, причому
![]()
є
коренем характеристичного рівняння
кратності
![]()
Підставимо в задане рівняння:
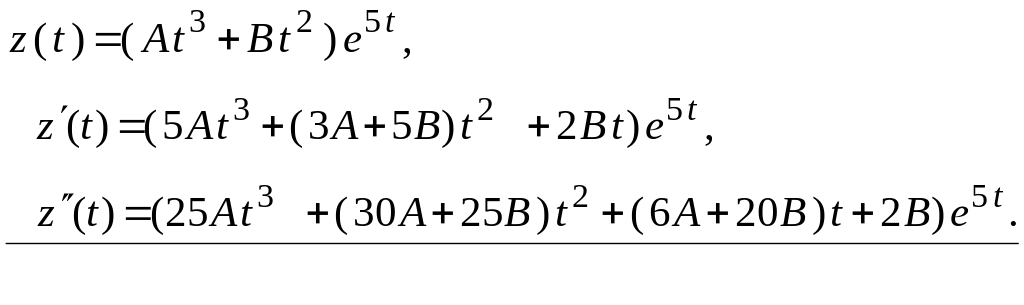
Порівнюючи відповідні коефіцієнти, дістанемо:
![]()
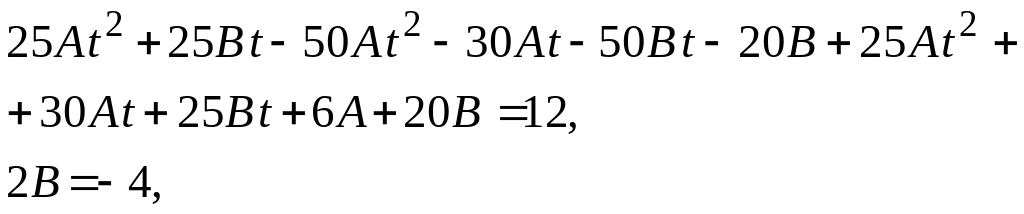
![]()
Отже,
![]() - загальний розв’язок заданого рівняння.
- загальний розв’язок заданого рівняння.
Для
знаходження сталих
![]() скористаємось початковими умовами:
скористаємось початковими умовами:
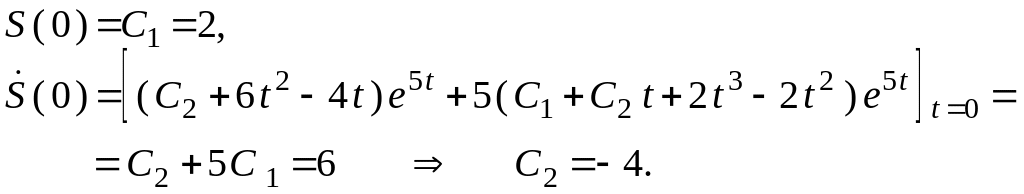
![]() -
шуканий розв’язок задачі Коші.
-
шуканий розв’язок задачі Коші.
Задача
7.
Нехай
![]() права частина лінійного неоднорідного
диференціального рівняння четвертого
порядку зі сталими коефіцієнтами,
права частина лінійного неоднорідного
диференціального рівняння четвертого
порядку зі сталими коефіцієнтами,
![]()
![]() -
корені відповідного характеристичного
рівняння.
-
корені відповідного характеристичного
рівняння.
Записати вигляд загального розв’язку цього рівняння, користуючись методом невизначених коефіцієнтів ( числових значень коефіцієнтів не шукати ).
Розв’язання. За теоремою про структуру загального розв’язку лінійного неоднорідного диференціального рівняння зі сталими коефіцієнтами
маємо:
![]() ,
причому
,
причому
![]() .
.
Для
того, щоб записати
![]() скористаємось принципом суперпозиції
розв’язків. Оскільки права частина
скористаємось принципом суперпозиції
розв’язків. Оскільки права частина
![]() є сумою двох функцій
є сумою двох функцій
![]() та
та
![]() то
=
то
=![]() +
+![]() .
.
Розглянемо
![]() ;
;
![]() не є коренем характеристичного рівняння,
тому
=
не є коренем характеристичного рівняння,
тому
=
![]()
Для
![]() також
не є коренем характеристичного рівняння,
тому
також
не є коренем характеристичного рівняння,
тому
=
![]()
Отже, остаточно:
![]() +
+
+
![]() +
+
![]() -
-
загальний розв’язок відповідного ЛНДР.
Задача 8. Записати загальний розв’язок лінійного рівняння
![]()
Значень коефіцієнтів в частинному розв’язку не знаходити.
Розв’язання. Зрозуміло, що характеристичне рівняння
![]() має
корінь
має
корінь
![]() Звідси отримаємо:
Звідси отримаємо:
![]() Отже,
Отже,
![]()
Загальний розв’язок відповідного однорідного рівняння:
![]()
Оскільки права частина рівняння є сумою чотирьох додатків,
то відповідно можемо записати :
![]()
![]() =
=
![]()
![]()
![]() =
=
![]()
![]()
![]()
![]()
![]()
Остаточно, загальний розв’язок ЛНДР має вигляд :
![]()
![]() +
+
+
![]() +
+
![]() +
+
![]() + G.
+ G.
Задача 9. Розв’язати задачу Коші для лінійного неоднорідного диференціального рівняння зі сталими коефіцієнтами:
![]()
Розв’язання.
Загальний розв’язок заданого ЛНДР
другого порядку будемо шукати у вигляді
![]() Для знаходження
Для знаходження
![]() складемо характеристичне рівняння
відповідного однорідного рівняння:
складемо характеристичне рівняння
відповідного однорідного рівняння:
![]() його корені
його корені
![]() Отже, фундаментальну систему розв’язків
рівняння
Отже, фундаментальну систему розв’язків
рівняння
![]() складають функції
складають функції
![]()
![]() а загальний розв’язок – це їх лінійна
комбінація:
а загальний розв’язок – це їх лінійна
комбінація:
![]()
Знайдемо
частинний розв’язок
![]() неоднорідного рівняння. Оскільки права
частина
неоднорідного рівняння. Оскільки права
частина
![]() не має спеціального вигляду, то
використаємо метод варіації довільних
сталих ( Лагранжа ):
=
не має спеціального вигляду, то
використаємо метод варіації довільних
сталих ( Лагранжа ):
=
![]() ,
де похідні невідомих функцій
,
де похідні невідомих функцій
![]() ,
,![]() знайдемо, розв’язавши систему :
знайдемо, розв’язавши систему :
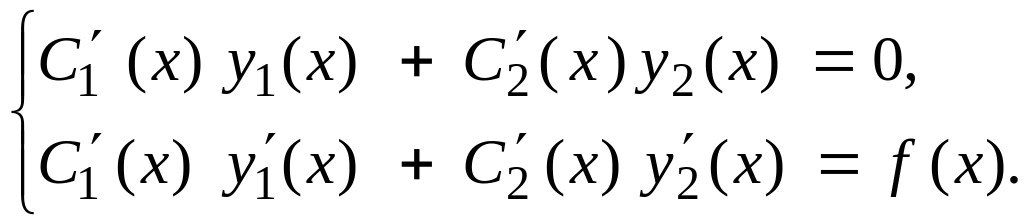
Отже,
=
![]() ;
;
 або
або
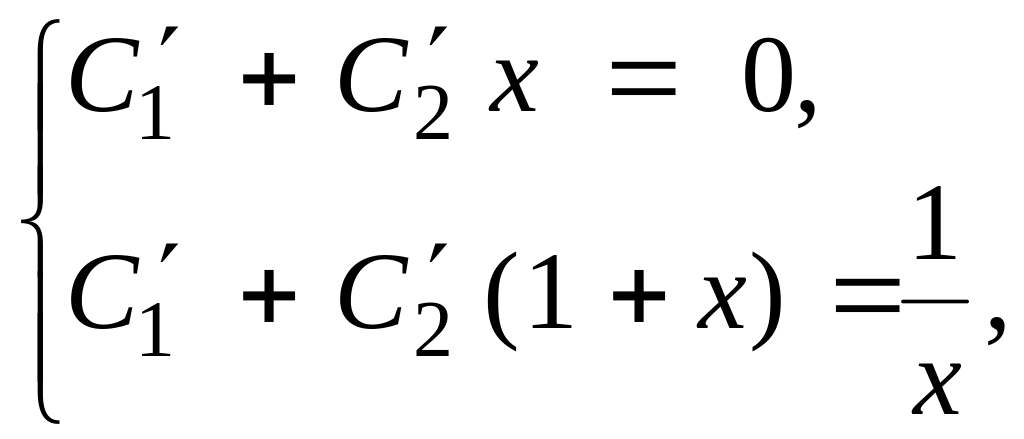 (
(![]()
Маємо,

=
![]() ,
,
![]() -
загальний розв’язок заданого рівняння.
-
загальний розв’язок заданого рівняння.
Для
знаходження довільних сталих використаємо
початкові умови:
![]()
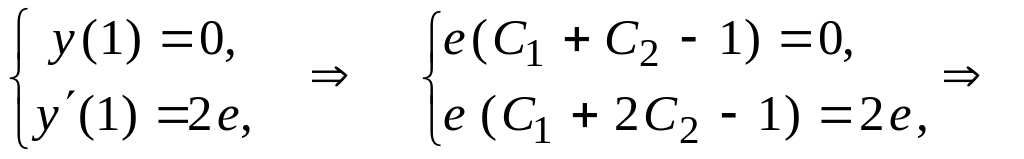
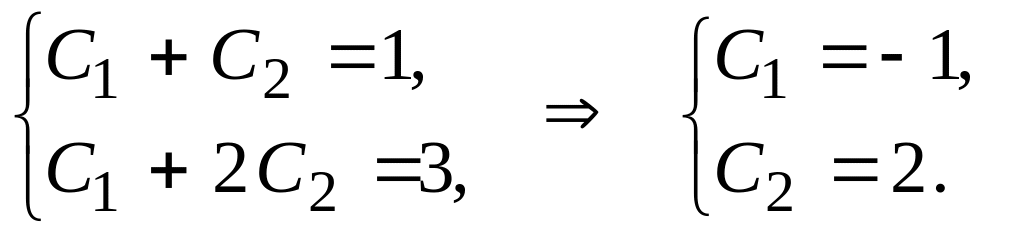
![]() -
розв’язок задачі Коші.
-
розв’язок задачі Коші.
Задача
10.
Для задачі Коші
![]()
а) знайти розв’язок в аналітичній формі, застосовуючи відомі методи інтегрування;
б)
побудувати наближення Пікара
![]() за схемою
за схемою
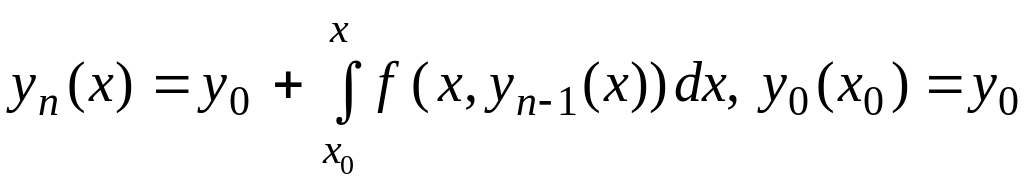 ,
,
та порівняти розв’язки пунктів а) і б).
Розв’язання.
а). Маємо лінійне рівняння ( в даному
випадку зі сталими коефіцієнтами та
спеціальним виглядом правої частини
). Як неважко перевірити, точний розв’язок
цієї задачі Коші
![]() .
.
б).
Оскільки виконуються всі умови теореми
про існування та єдиність розв’язку
задачі Коші (перевірте), то послідовність
Пікара в деякому околі точки
![]() рівномірно збігається до точного
розв’язку. Відмітимо, що ряд Маклорена
функції
рівномірно збігається до точного
розв’язку. Відмітимо, що ряд Маклорена
функції
![]() має вигляд:
має вигляд:
![]() ,
і рівність має місце для будь-якого
,
і рівність має місце для будь-якого
![]() .
.
Побудуємо
послідовність
наближень Пікара, де
![]()
Маємо:
![]() ,
,
![]() ,
,
![]()
![]() ,
,
![]()
![]()
![]() .
.
Таким
чином,
![]() .
.
Задача 11. а). Знайти частинний розв’язок рівняння
![]()
у
вигляді ряду за степенями
![]() .
Суму ряду виразити через елементарні
функції.
.
Суму ряду виразити через елементарні
функції.
б). Знайти другий частинний розв’язок, використовуючи формулу Остроградського – Ліувілля. Записати загальний розв’язок рівняння.
Розв’язання.
Оскільки
![]() ,
то частинний розв’язок рівняння будемо
шукати у вигляді ряду Маклорена:
,
то частинний розв’язок рівняння будемо
шукати у вигляді ряду Маклорена:
![]() .
.
Із
початкових умов маємо:
![]() .
Оскільки
.
Оскільки
![]() ,
то
,
то
![]() .
Далі маємо:
.
Далі маємо:
![]() .
Зрозуміло, що при
.
Зрозуміло, що при
![]() похідні вищих порядків функції
похідні вищих порядків функції
![]() при умові, що
при умові, що
![]() будуть дорівнювати нулю. Тому частинним
розв’язком
будуть дорівнювати нулю. Тому частинним
розв’язком
![]() цієї задачі є многочлен
цієї задачі є многочлен
![]() .
.
Для знаходження другого частинного розв’язку використаємо формулу Остроградського – Ліувілля:
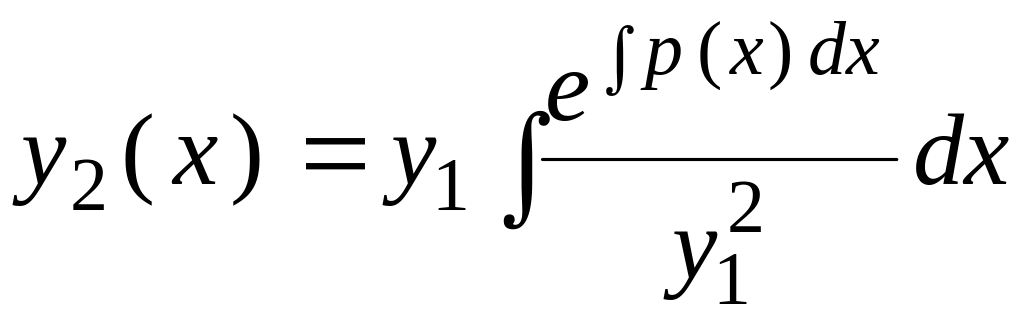
для
розв’язку рівняння
![]() ,
тобто
,
тобто
![]() ,
де
,
де
первісну
функції
![]() можна записати у вигляді ряду ( Якого?
).
можна записати у вигляді ряду ( Якого?
).
Отже, загальний розв’язок даного рівняння має вигляд:
![]() .
.
Задача 12. Знайти загальний або частинний розв’язок системи диференціальних рівнянь.
а). Однорідну систему розв’язати методом Ейлера:
![]()
Розв`язання.
Запишемо матрицю системи
![]() та її характеристичне рівняння
та її характеристичне рівняння
![]() ,
тобто
,
тобто
![]() .
.
Корені
цього рівняння 1,2
=
2
j. Знайдемо власний вектор матриці А,
який відповідає власному значенню
![]() :
:
![]()
Звідси
![]() .
Тому
.
Тому
![]()
![]() .
.
Отже,
![]() є комплексним розв’язком заданої
системи. Відомо, що окремо дійсна та
уявна частини отриманого розв’язку є
дійсними розв’язками системи. Тому :
є комплексним розв’язком заданої
системи. Відомо, що окремо дійсна та
уявна частини отриманого розв’язку є
дійсними розв’язками системи. Тому :
![]() Таким
чином, маємо два дійсних розв’язки
заданої системи:
Таким
чином, маємо два дійсних розв’язки
заданої системи:
![]()
![]()
![]()
а загальний розв’язок системи має вигляд:
![]()
Тепер
знайдемо той розв’язок, для якого
![]() .
.
Маємо:
![]() ,
звідки
,
звідки
![]() .
Тоді
.
Тоді
![]() – шуканий розв’язок.
– шуканий розв’язок.
б).
Неоднорідну систему
![]() розв’яжемо методом зведення до одного
рівняння другого порядку:
розв’яжемо методом зведення до одного
рівняння другого порядку:
Розв`язання.
Продиференціюємо по t
перше
рівняння системи; дістанемо:
![]() ,
де
,
де
![]() згідно другого рівняння. Отже,
згідно другого рівняння. Отже,
![]() .
.
З
першого рівняння системи (того, що
диференціювали) знайдемо
![]() і підставимо в
і підставимо в
![]() :
:
![]() .
.
Одержали
систему:
![]()
Розв’яжемо перше рівняння системи - лінійне неоднорідне диференціальне рівняння другого порядку зі сталими коефіцієнтами та спеціальним виглядом правої частини.
Корені
відповідного характеристичного
рівняння
![]()
![]() .
Частинний розв’язок цього рівняння за
виглядом правої частини шукатимемо у
вигляді:
.
Частинний розв’язок цього рівняння за
виглядом правої частини шукатимемо у
вигляді:

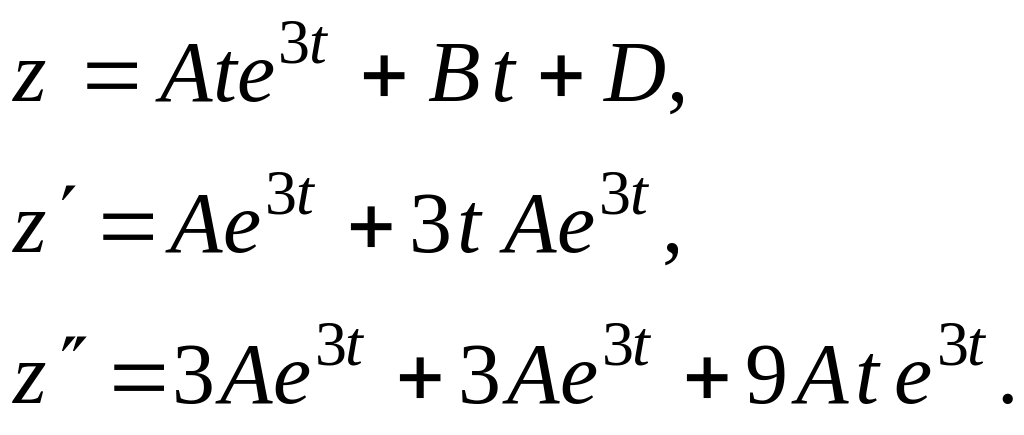
____________________________

![]()
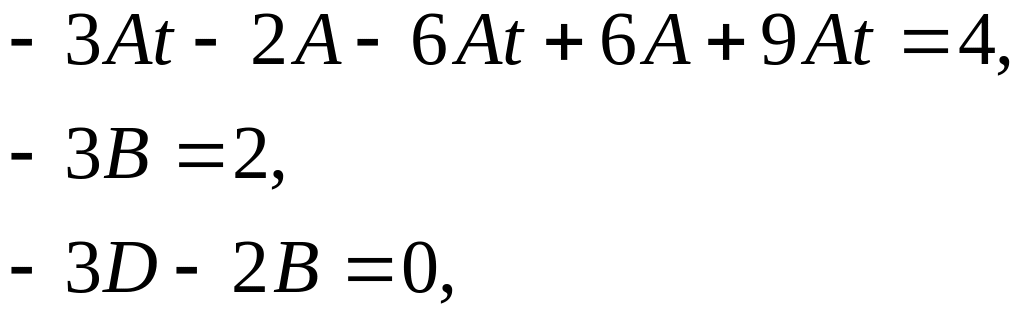
тобто
![]() Тоді маємо:
Тоді маємо:

Задача 13. Визначити криві, для яких абсциса точки перетину довільної дотичної з віссю абсцис вдвоє менше абсциси точки дотику.
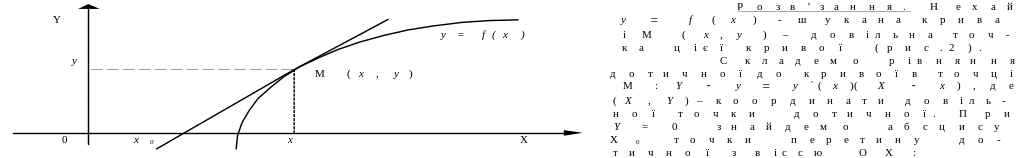 Рис.
2.
Рис.
2.
![]() ,
тобто
,
тобто
![]() .
.
За
умовою задачі
![]() ,
звідки
,
звідки
![]() ,
або
,
або![]() .
.
Дістали
диференціальне рівняння першого порядку.
Отже, маємо його загальний розв’язок:
![]() .
.
Таким
чином, шукані криві - це параболи
![]() ,
,
де
С
– довільна стала,
![]() .
.
Задача 14. Матеріальна точка маси m = 1кг падає на землю з деякої висоти. Знайти закон руху точки, якщо опір повітря пропорційний швидкості падіння (коефіцієнт пропорційності (к=2). Який шлях пройде точка через 3 секунди після початку руху.
Ц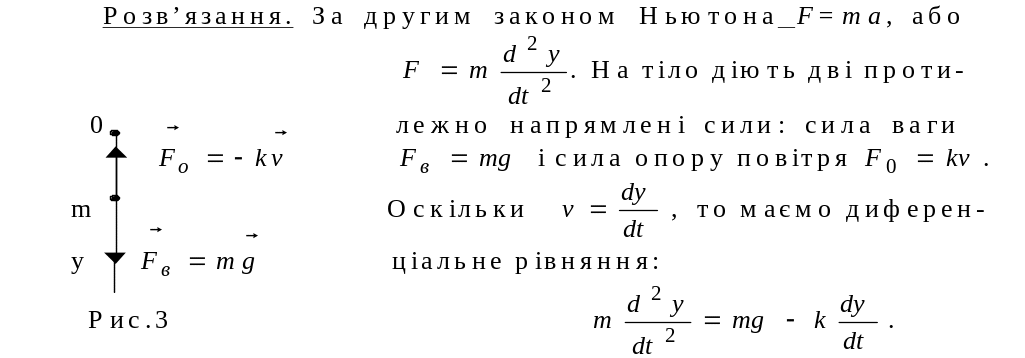 е
лінійне неоднорідне диференціальне
рівняння другого порядку зі сталими
коефіцієнтами:
е
лінійне неоднорідне диференціальне
рівняння другого порядку зі сталими
коефіцієнтами:
![]() .
.
Характеристичне
рівняння
![]() має корені
має корені
![]() .
.
Загальний
розв’язок ЛНДР:
![]() ,
де частинний розв’язок z(t)=At.
Знайдемо
,
де частинний розв’язок z(t)=At.
Знайдемо
![]() та підставимо в
та підставимо в
одержане
рівняння, звідки
![]() .
Отже,
.
Отже,
![]() .
.
Використаємо початкові умови для знаходження С1, С2:
![]()
![]()
![]()
Отже,
закон руху матеріальної точки:
![]() .
.
Якщо
t
=
3c
,
m
=
1кг,
к =
2, то маємо
![]() .
.
Задача
15. Розглянемо
нестаціонарний режим в електричному
ланцюгу з параметрами
![]() ,
які будемо вважати сталими. При його
дослідженні розрізняють задачі з
нульовими та ненульовими початковими
умовами.
,
які будемо вважати сталими. При його
дослідженні розрізняють задачі з
нульовими та ненульовими початковими
умовами.
а).
Задачі
з нульовими початковими умовами. До
таких задач відносять випадки, коли до
електричного ланцюга, який знаходиться
в положенні спокою, в момент часу
![]() підключається напруга. В цьому випадку
до моменту включення напруга струму
та заряди на конденсаторах ланцюга
дорівнюють нулю.
підключається напруга. В цьому випадку
до моменту включення напруга струму
та заряди на конденсаторах ланцюга
дорівнюють нулю.
Нехай
в ланцюгу
( рис. 4 ) в момент часу
підключена напруга
![]() .
В початковий момент струм в контурі і
напруга на конденсаторі дорівнюють
нулю. Під дією напруги
по ланцюгу потече струм
.
В початковий момент струм в контурі і
напруга на конденсаторі дорівнюють
нулю. Під дією напруги
по ланцюгу потече струм
![]() .
Визначити закон зміни струму
.
Визначити закон зміни струму
Розв’язання. Складемо інтегро – диференціальне рівняння рівноваги ланцюга. За другим законом Кірхгофа маємо:
![]() ,
де
,
де
![]() -
падіння напруги на активному опорі;
-
падіння напруги на активному опорі;
![]() -
падіння напруги на індуктивності;
-
падіння напруги на індуктивності;
![]() -
падіння напруги на ємності;
-
падіння напруги на ємності;
- струм нестаціонарного режиму.

Рис. 4.
Продиференціюємо по t одержане інтегро–диференціальне рівняння:
![]() ,
де
,
де
![]()
б). Задачі з ненульовими початковими умовами. До таких задач відносять задачі, коли початкові значення струмів у вітках, які містять індуктивність і напругу на конденсаторах, при відмінні від нуля. Такі умови з’являються у задачах, коли відбувається яке – небудь переключення в ланцюгу, який знаходиться під напругою.
Нехай
в ланцюгу (рис. 5) в момент
опір
![]() шунтується рубильником К. В результаті
шунтування опору
струм в ланцюгу змінюється. Визначити
закон зміни струму.
шунтується рубильником К. В результаті
шунтування опору
струм в ланцюгу змінюється. Визначити
закон зміни струму.
Розв’язання. За другим законом Кірхгофа запишемо інтегро – диференціальне рівняння:
![]() ,
де
,
де
![]() - початкова напруга на ємності, яка
обумовлена електричним зарядом ємності
в момент
.
- початкова напруга на ємності, яка
обумовлена електричним зарядом ємності
в момент
.
Р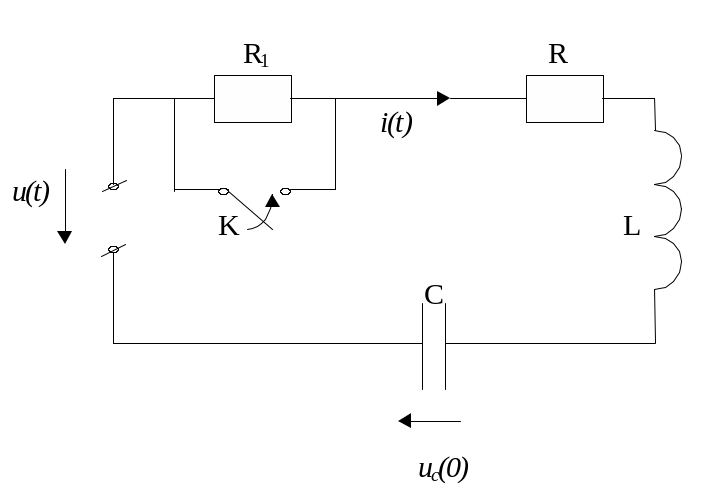 ис.
5.
ис.
5.
Відповідна задача Коші буде мати вигляд:
,
![]()
де
![]() - струм у момент часу
.
- струм у момент часу
.
ОСНОВНІ
ПЕРВІСНІ (
![]() сталі )
сталі )
![]()
![]()
![]()
![]()
