
- •Введение
- •Лабораторная работа №1 «Графический метод».
- •Образец оформления отчета лабораторной работы №1 «Графический метод».
- •Задача.
- •Решение.
- •Лабораторная работа №2 «Симплекс-метод».
- •Образец оформления отчета лабораторной работы №2 «Симплекс-метод».
- •Задача.
- •Решение.
- •Лабораторная работа №3 «Двойственная задача».
- •Образец оформления отчета лабораторной работы №3 «Двойственная задача».
- •Задача.
- •Решение.
- •Лабораторная работа №4 «Целочисленное линейное программирование».
- •Лабораторная работа №5 «Транспортная задача».
- •Образец оформления отчета лабораторной работы №5 «Транспортная задача».
- •Задача.
- •Решение.
- •Список рекомендуемой литературы
- •Содержание
Лабораторная работа №3 «Двойственная задача».
Цель: изучение принципа построения двойственной задачи и практическое применение методик ее решения.
С каждой задачей линейного программирования тесно связана другая линейная задача, называемая двойственной; первоначальная задача называется исходной или прямой.
Связь исходной и двойственной задач заключается, в частности, в том, что решение одной из них может быть получено .непосредственно из решения другой.
Хорошо разработанный математический аппарат линейного программирования позволяет не только получать с помощью эффективных вычислительных процедур оптимальный план, но и делать ряд экономически содержательных выводов, основанных на свойствах задачи, двойственной к исходной задачи линейного программирования.
Каждая из задач двойственной пары фактически является самостоятельной задачей линейного программирования и может быть решена независимо от другой. Однако при определении симплексным методом оптимального плана одной из задач находится решение и другой задачи.
Для решения двойственной задачи студент должен:
изучить теоретический материал;
составить математическую модель исходной задачи;
составить математическую модель двойственной задачи по отношению к исходной;
найти решение (оптимальный план) двойственной задачи, используя симплекс-метод;
проанализировать полученное решение, проверив его правильность на ЭВМ;
оформить решение задачи в виде отчета по лабораторным работам.
Постановка и методика решения подобных задач рассмотрена в образце оформления отчета лабораторной работы №3 (стр. 35).
Задание: составить двойственную задачу к исходной и решить ее симплекс-методом.
В качестве исходной задачи принимается задача из Лабораторной работы №2 согласно своему варианту.
Образец оформления отчета лабораторной работы №3 «Двойственная задача».
Задание: составить двойственную задачу к исходной и решить ее симплекс-методом.
Задача.
Предприятие изготавливает и реализует два вида продукции – P1 и P2. Для производства продукции используются два вида ресурсов – сырье и труд. Максимальные запасы этих ресурсов в сутки составляют 14 и 26 единиц соответственно. Расход ресурсов на изготовление каждого вида продукции, запасы и оптовые цены продукции приведены в таблице.
Ресурсы |
Расходы ресурсов на 1 ед. продукции |
Запас ресурсов, ед. |
|
P1 |
P2 |
||
Сырье |
1 |
3 |
14 |
Труд |
4 |
2 |
26 |
Оптовая цена |
3 |
3 |
|
Известно, что суточный спрос на продукцию P1, никогда не превышает спроса на продукцию P2 более чем на 5 ед., а спрос на продукцию P2 никогда не превышает 4 ед. в сутки.
Как спланировать выпуск продукции предприятия, чтобы доход от ее реализации был максимальным?
Решение.
Составим математическую модель прямой задачи. Предположим, что предприятию следует изготовить Х1 ед. продукции P1 и Х2 ед. продукции P2. Поскольку имеются нормы затрат ресурсов на одно изделие данного вида продукции и общее количество имеющихся ресурсов каждого вида, а также величина суточного спроса на реализуемую продукцию, то должна выполняться следующая система ограничений:
Общая прибыль от реализации произведенной продукции составит:
По своему экономическому содержанию переменные Х1 и Х2 могут принимать только лишь неотрицательные значения:
Теперь составим по отношению к этой прямой задачи двойственную ей задачу.
Число переменных в двойственной задаче равно числу неравенств в системе ограничений прямой задачи, т.е. равно четырем:
![]()
Коэффициентами в целевой функции двойственной задачи являются свободные члены системы ограничений прямой задачи, т.е. 14, 26, 5 и 4. Целевая функция исходной задачи задана на максимум, поэтому в двойственной задаче целевая функция задается на минимум:
![]()
Матрица ограничений двойственной задачи получаем путем транспонирования матрицы ограничений прямой задачи:

![]()
Коэффициенты целевой функции прямой задачи становятся свободными членами ограничений двойственной задачи, т.е. 3 и 3.
Таким образом, двойственной по отношению к исходной прямой задачи является следующая задача.
Требуется найти
неотрицательные числа
![]() ,
обращающие в минимум целевую функцию
,
обращающие в минимум целевую функцию
,
при условиях:
![]()
Перейдем от задачи на минимум к задаче на максимум:
![]()
при условиях
![]()
Запишем полученную задачу в канонической форме, введя дополнительные переменные Y5 и Y6:
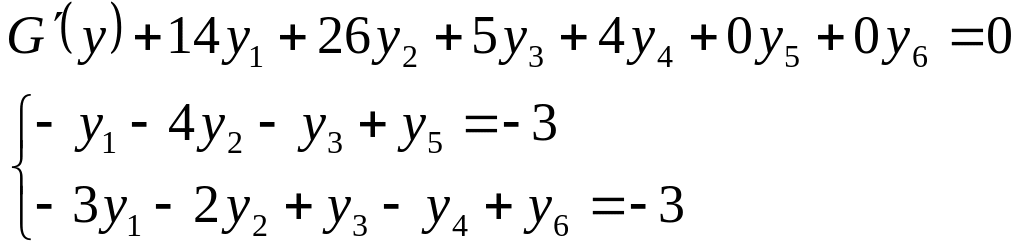
Так как среди свободных членов системы уравнений содержатся отрицательные числа, то для решения данной задачи линейного программирования воспользуемся двойственным симплекс-методом. Все итерации вычислительного процесса последовательно запишем одна за другой в виде симплексной таблицы.
i |
Базис |
Cj |
bi |
Y1 |
Y2 |
Y3 |
Y4 |
Y5 |
Y6 |
Оценка |
|
1 |
Y5 |
0 |
-3 |
-1 |
-4 |
-1 |
0 |
1 |
0 |
3 |
---> max |
2 |
Y6 |
0 |
-3 |
-3 |
-2 |
1 |
-1 |
0 |
1 |
3 |
|
0 |
G' |
- |
0 |
14 |
26 |
5 |
4 |
0 |
0 |
|
|
|
|
|
|
14 |
6,5 |
5 |
|
|
|
|
|
|
|
|
|
|
|
min |
|
|
|
|
|
i |
Базис |
Cj |
bi |
Y1 |
Y2 |
Y3 |
Y4 |
Y5 |
Y6 |
Оценка |
|
1 |
Y3 |
-5 |
3 |
1 |
4 |
1 |
0 |
-1 |
0 |
|
|
2 |
Y6 |
0 |
-6 |
-4 |
-6 |
0 |
-1 |
1 |
1 |
6 |
---> max |
0 |
G' |
- |
-15 |
9 |
6 |
0 |
4 |
5 |
0 |
|
|
|
|
|
|
2,25 |
1 |
|
4 |
|
|
|
|
|
|
|
|
|
min |
|
|
|
|
|
|
i |
Базис |
Cj |
bi |
Y1 |
Y2 |
Y3 |
Y4 |
Y5 |
Y6 |
Оценка |
|
1 |
Y3 |
-5 |
-1 |
-1,667 |
0 |
1 |
-0,667 |
-0,333 |
0,6667 |
1 |
---> max |
2 |
Y2 |
-26 |
1 |
0,6667 |
1 |
0 |
0,1667 |
-0,167 |
-0,167 |
|
|
0 |
G' |
- |
-21 |
5 |
0 |
0 |
3 |
6 |
1 |
|
|
|
|
|
|
3 |
|
|
4,5 |
18 |
|
|
|
|
|
|
|
min |
|
|
|
|
|
|
|
i |
Базис |
Cj |
bi |
Y1 |
Y2 |
Y3 |
Y4 |
Y5 |
Y6 |
|
|
1 |
Y1 |
-14 |
0,6 |
1 |
0 |
-0,6 |
0,4 |
0,2 |
-0,4 |
|
|
2 |
Y2 |
-26 |
0,6 |
0 |
1 |
0,4 |
-0,1 |
-0,3 |
0,1 |
|
|
0 |
G' |
- |
-24 |
0 |
0 |
3 |
1 |
5 |
3 |
|
|
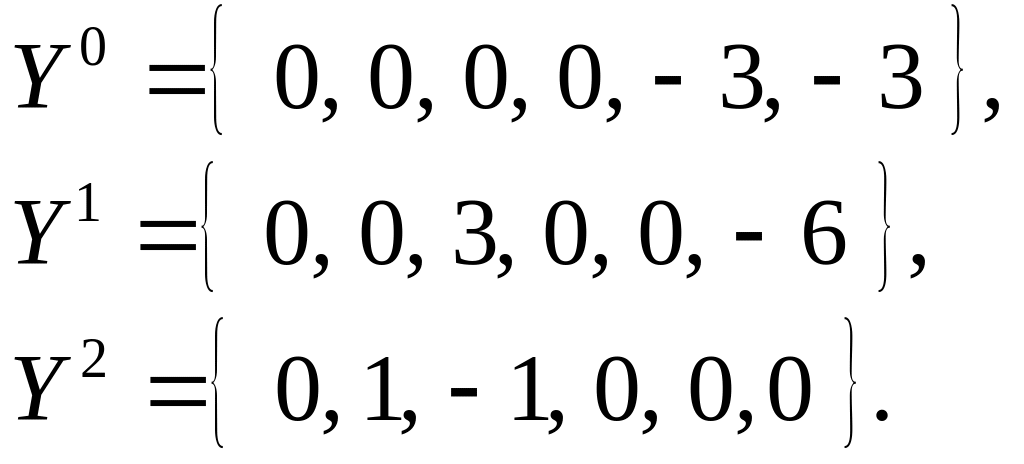
![]()
Вернемся к двойственной задаче на минимум:
![]()
