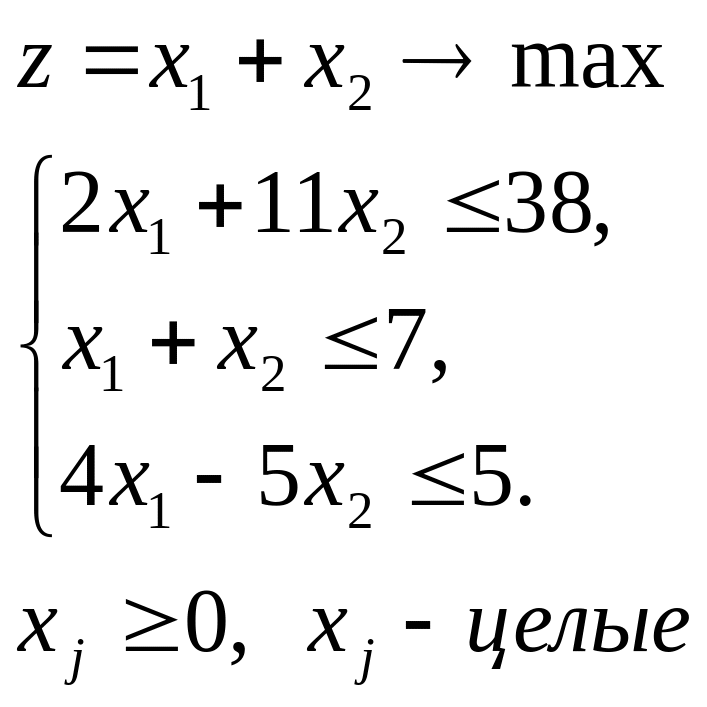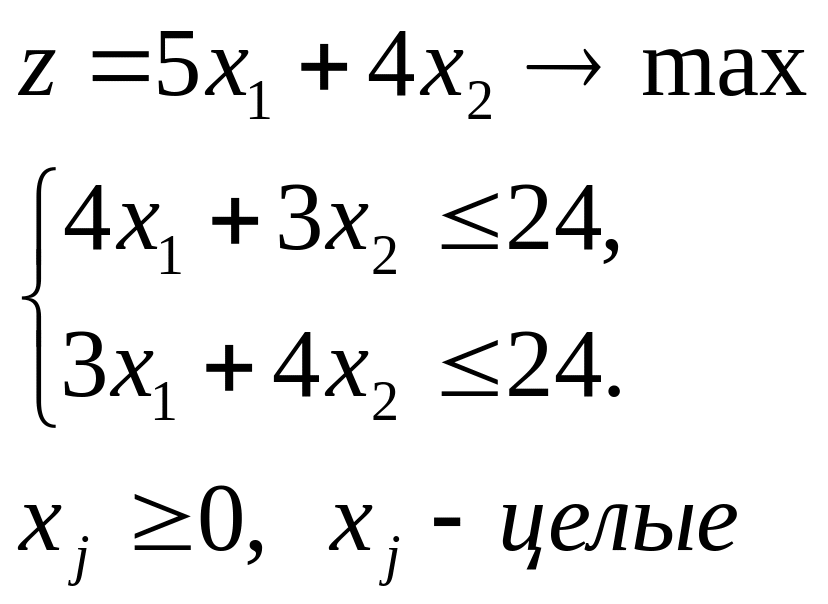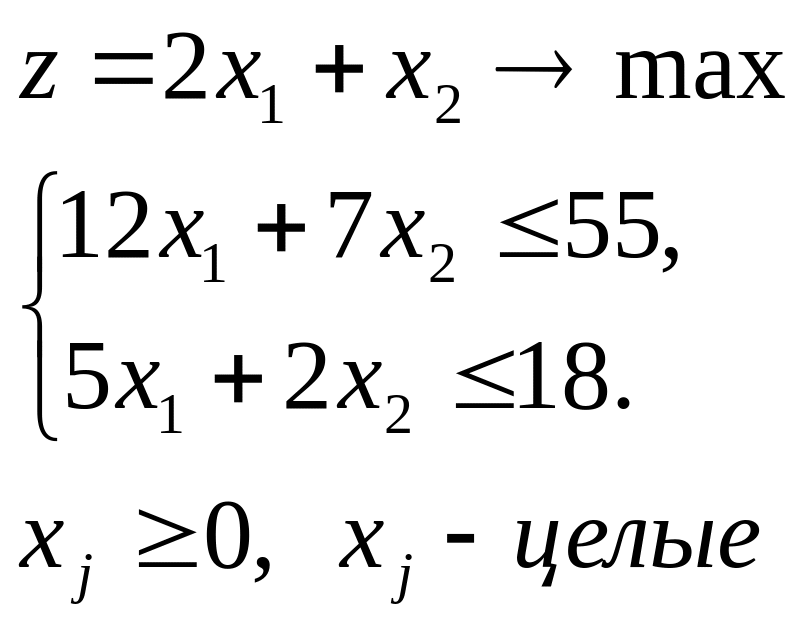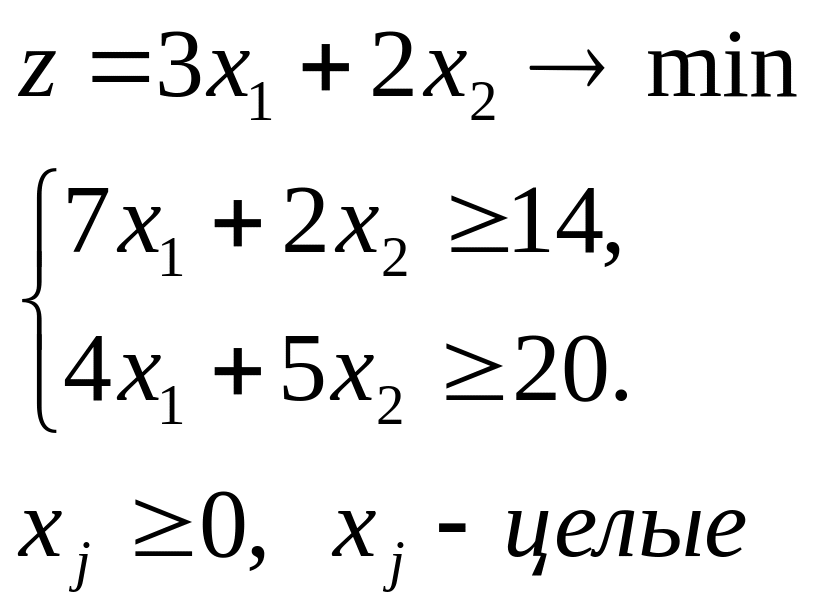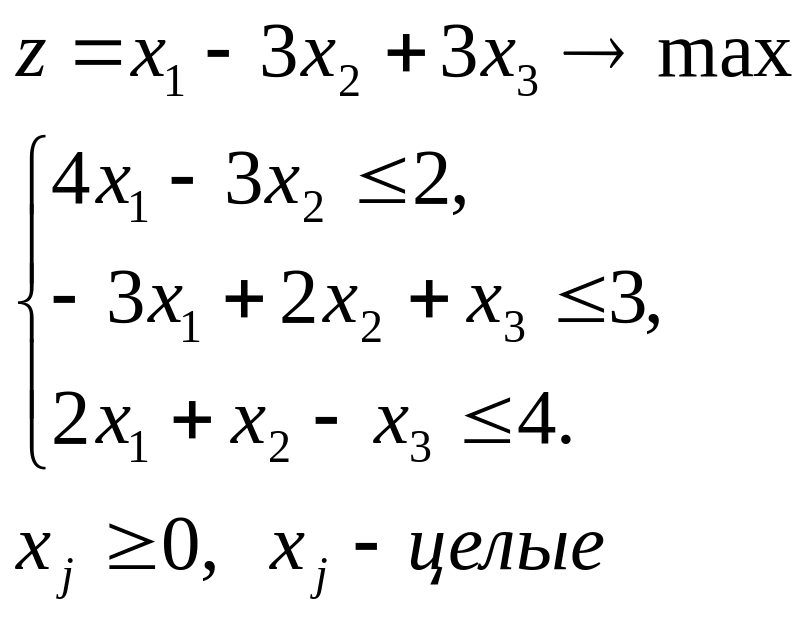Лабораторная работа №4 «Целочисленное линейное программирование».

Цель: изучение и практическое применение методик решения задач целочисленного линейного программирования.

Модели целочисленного линейного программирования в области экономики и управления включают в себя задачи, в которых на искомые переменные накладываются условия целочисленности, а также область допустимых решений этих задач конечна. Такими задачами являются задачи с переменными, определяющими количество единиц неделимой продукции, например:

• задачи распределения станков, механизмов по видам работ,

• автомобилей по маршрутам,

• распределение производственных заданий между предприятиями,

• раскрой материалов,

• распределение судов по линиям, самолетов по рейсам,

• задачи по производству неделимой продукции и др.

Требование целочисленности переменных приводит к необходимости применения специальных методов их решения. Среди них наиболее распространенными являются метод отсечения (или метод Гомори) и метод ветвей и границ.

Для решения задачи целочисленного линейного программирования студент должен:

• изучить теоретический материал;

• решить задачу без учета целочисленности;

• методом отсечения (методом Гомори) или методом ветвей и границ (метод выбирается согласно своему варианту) найти целочисленное решение;

• проанализировать полученное решение, проверив его правильность на ЭВМ;

• оформить решение задачи в виде отчета по лабораторным работам.

Постановка и методика решения подобных задач рассмотрена в образце оформления отчета лабораторной работы №4 (метод ветвей и границ – стр. 45, метод Гомори – стр. 49).

Задание: указанным методом найти оптимальное решение задачи целочисленного линейного программирования.

Методом ветвей и границ найти оптимальное решение задачи:

4.1.	4.2.
4.3.

Методом Гомори найти оптимальное решение задачи:

4.4.	4.5.
4.6.

4.7. Пароход может быть использован для перевозки четырех наименований груза, масса, объем и цена единицы каждого из которых приведены в таблице:

Параметры единицы груза	Номер груза
	1	2	3	4
Масса (т)	80	62	92	82
Объем (м^3)	100	90	96	110
Цена (у.е.)	4,4	2,7	3,2	2,8

На пароход может быть погружено не более 800 т груза общим объемом, не превышающим 600 м³.

Определить, сколько единиц каждого груза следует поместить на пароход, чтобы при этом общая стоимость размещенного груза была максимальной.

4.8.	4.9.
4.10.	4.11.
4.12.

Методом ветвей и границ найти оптимальное решение задачи:

4.13. Для изготовления столов и шкафов мебельная фабрика использует необходимые ресурсы. Нормы затрат ресурсов на одно изделие данного вида, прибыль от реализации одного изделия и общее количество имеющихся ресурсов каждого вида приведены в следующей таблице.

Определить, сколько столов и шкафов фабрике следует изготовить, чтобы прибыль от их реализации была максимальной.

Ресурсы	Нормы затрат ресурсов на одно изделие		Общее количество ресурсов
	стол	шкаф
Древесина (м^3) I вида	0,2	0,1	50
Древесина (м^3) II вида	0,1	0,3	70
Трудоемкость (человеко – ч.)	1,2	1,5	380
Прибыль от реализации одного изделия, д. ед.	8	6

4.14.

4.15.

4.16. Для приобретения оборудования, размещаемого на производственной площади 38 м², фирма выделяет 20 млн. руб. Имеются единицы оборудования двух типов: типа А стоимостью 5 млн. руб., требующее производственную площадь 8 м² и имеющее производительность 7 тыс. единиц продукции за смену, и типа Б – стоимостью 2 млн. руб., занимающее площадь 4 м² и дающее за смену 3 тыс. единиц продукции. Требуется рассчитать оптимальный вариант приобретения оборудования, обеспечивающий максимум производительности участка.

Методом Гомори найти оптимальное решение задачи:

4.17.

4.18.

4.19.

Методом ветвей и границ найти оптимальное решение задачи:

4.20.	4.21.
4.22.	4.23.
4.24.	4.25.
4.26.

Методом Гомори найти оптимальное решение задачи:

4.27.	4.28.
4.29.	4.30.

Образец оформления отчета лабораторной работы №4

«Целочисленное линейное программирование».

(Метод ветвей и границ)

Задание: указанным методом найти оптимальное решение задачи целочисленного линейного программирования.

Задача.

Методом ветвей и границ найти оптимальное решение задачи

при ограничениях

Решение.

Для наглядности решение осуществим графическим методом. ОДР задачи является многоугольник OABC.

X₂

А

B

C

X₁

Z = 0

Z_max

В точке B находится максимальное значение функции:

при и

Поскольку значения неизвестных дробные, то разобьем по неизвестной x₂ ОДР задачи на две части. Одна будет содержать множество точек, у которых , а вторая – у которых . В результате получаем две новые задачи линейной оптимизации: №2 и №3 (исходная задача соответственно обозначим №1).

Области допустимых решений задач представим на графике.

X₂

X₁

А

B

C

D

E

x₂=3

x₂=4

Z = 0

Z_max

Из графика видно, что ни одна целочисленная точка исходной ОДР не потеряна.

ОДР задачи №2 является многоугольник OADEC. В точке E функция достигает максимального значения:

при и .

Решение задачи №2 не является целочисленным.

ОДР задачи №3 – пустое множество. Ограничения этой задачи противоречивы, и она не имеет решения.

Продолжим решения, для чего разобьем ОДР задачи №2 на два подмножества по неизвестной . В результате получим две новые задачи №4 и №5 с соответствующими дополнительными ограничениями и .

ОДР этих задач представим на графике.

X₂

X₁

А

B

C

D

E

x₂=3

x₂=4

Z = 0

Z_max

x₁=3

x₁=2

F

L

M

K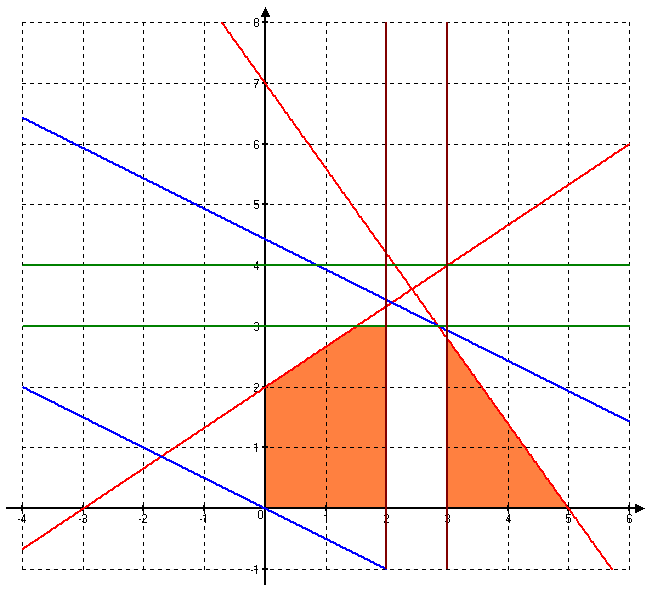

ОДР задачи №4 является многоугольник OADFK. Максимальное значение функции достигается в точке F:

при и .

Таким образом, получено целочисленное решение задачи №4.

ОДР задачи №5 является треугольник LMC. Максимальное значение функции достигается в точке L:

при и .

Так как значение функции целочисленного решения задачи №4 меньше , то дальнейшему разбиению на две задачи №6 и №7 подлежит задача №5 по нецелочисленной неизвестной .

Не проводя дополнительных построений, отметим, что ОДР задачи №6 с дополнительным ограничением не существует, а значение функции в оптимальном целочисленном решении задачи №7 с дополнительным ограничением равно 7, что меньше . Таким образом, целочисленное решение исходной задачи следующее:

Образец оформления отчета лабораторной работы №4

«Целочисленное линейное программирование».

(Метод Гомори)

Задание: указанным методом найти оптимальное решение задачи целочисленного линейного программирования.

Задача.

Методом Гомори найти оптимальное решение задачи

при ограничениях

Решение.

Отбрасывая условие целочисленности, находим симплекс-методом решение данной задачи. Для этого запишем исходную задачу в канонической форме, введя дополнительные переменные Х₃ и X₄:

Решение данной задачи можно проводить, используя лишь одну таблицу. В этой таблице последовательно запишем одна за другой все итерации вычислительного процесса.

i	Базис	cj	bi	x1	x2	x3	x4	Оценка
1	x3	0	35	7	5	1	0	7
2	x4	0	6	-2	3	0	1	2	min
0	Z	-	0	-1	-2	0	0
				1	2
					max
i	Базис	cj	bi	x1	x2	x3	x4	Оценка
1	x3	0	25	10,333333	0	1	-1,666667	2,4193548	min
2	x2	2	2	-0,666667	1	0	0,3333333
0	Z	-	4	-2,333333	0	0	0,6666667
				2,3333333
				max

i	Базис	cj	bi	x1	x2	x3	x4
1	x1	1	2,4193548	1	0	0,0967742	-0,16129
2	x2	2	3,6129032	0	1	0,0645161	0,2258065
0	Z	-	9,6451613	0	0	0,2258065	0,2903226

Данное решение не удовлетворяет условию целочисленности, поэтому формируем дополнительное ограничение для базисной переменной с наибольшей дробной частью.

Так как , то дополнительно ограничение составляем для базисной переменной x₂:

Таким образом, дополнительное ограничение будет иметь вид:

После преобразования данного ограничения и приведения его к каноническому виду получим:

Данное ограничение-равенство вводим в симплекс-таблицу и продолжаем решение задачи двойственным симплекс методом:

i	Базис	cj	bi	x1	x2	x3	x4	x5	Оценка
1	x1	1	2,4193548	1	0	0,0967742	-0,16129	0
2	x2	2	3,6129032	0	1	0,0645161	0,2258065	0
3	x5	0	-0,612903	0	0	-0,064516	-0,225806	1	0,6129032	max
0	Z	-	9,6451613	0	0	0,2258065	0,2903226	0
						3,5	1,2857143
							min
i	Базис	cj	bi	x1	x2	x3	x4	x5
1	x1	1	2,8571429	1	0	0,1428571	0	-0,714286
2	x2	2	3	0	1	0	0	1
3	x4	0	2,7142857	0	0	0,2857143	1	-4,428571
0	Z	-	8,8571429	0	0	0,1428571	0	1,2857143

Данное оптимальное решение в очередной раз не удовлетворяет условию целочисленности, поэтому снова формируем дополнительное ограничение:

Таким образом, дополнительное ограничение будет иметь вид:

После преобразования данного ограничения и приведения его к каноническому виду получим:

Данное ограничение-равенство вводим в симплекс-таблицу и продолжаем решение задачи двойственным симплекс методом:

i	Базис	cj	bi	x1	x2	x3	x4	x5	x6	Оценка
1	x1	1	2,8571429	1	0	0,1428571	0	-0,714286	0
2	x2	2	3	0	1	0	0	1	0
3	x4	0	2,7142857	0	0	0,2857143	1	-4,428571	0
4	x6	0	-0,857143	0	0	-0,142857	0	-0,285714	1	0,857143	max
0	Z	-	8,8571429	0	0	0,1428571	0	1,2857143	0
						1		4,5
						min

i	Базис	cj	bi	x1	x2	x3	x4	x5	x6
1	x1	1	2	1	0	0	0	-1	1
2	x2	2	3	0	1	0	0	1	0
3	x4	0	1	0	0	0	1	-5	2
4	x3	0	6	0	0	1	0	2	-7
0	Z	-	8	0	0	0	0	1	1

Поскольку переменные x₁ и x₂ в данном оптимальном решении принимают целые значения, то найденное решение будет являться оптимальным для исходной задачи целочисленного линейного программирования.