Тема 4: линейные электрические цепи переменного

ТОКА

Переменным называется периодически изменяющийся по направлению и амплитуде электрический ток. При этом, если переменный ток изменяется по синусоидальному закону - он называется синусоидальным, а если нет - несинусоидальым. Электрическая цепь с таким током называется цепью переменного (синусоидального или несинусоидального) тока.

Электротехнические устройства переменного тока находят широкое приме- нение в различных областях народного хозяйства, при генерировании, передаче и трансформировании электрической энергии, в электроприводе, бытовой тех- нике, промышленной электронике, радиотехнике и т. д.

Преимущественное распространение электротехнических устройств пере- менного синусоидального тока обусловлено рядом причин.

Современная энергетика основана на передаче энергии на дальние расстояния при помощи электрического тока. Обязательным условием такой передачи является возможность простого и с малыми потерями энергии преобразова- ния тока. Такое преобразование осуществимо лишь в электротехнических устройствах переменного тока — трансформаторах. Вследствие громадных преимуществ трансформирования в современной электроэнергетике приме- няется прежде всего синусоидальный ток.

Большим стимулом для разработки и развития электротехнических уст- ройств синусоидального тока является возможность получения источников электрической энергии большой мощности. У современных турбогенераторов тепловых электростанций мощность равна100-1500 МВт на один агрегат, боль-

шие мощности имеют и генераторы гидростанций.

К наиболее простым и дешевым электрическим двигателям относятся асин- хронные двигатели переменного синусоидального тока, в которых отсутствуют движущиеся электрические контакты. Для электроэнергетических установок (в частности, для всех электрических станций) в России и в большинстве стран мира принята стандартная частота 50 Гц (в США - 60 Гц). Причина такого выбора простые: понижение частоты неприемлемо, так как уже при частоте тока 40 Гц лампы накаливания заметно для глаза мигают; повышение часто- ты нежелательно, так как пропорционально частоте растет ЭДС само индукции, отрицательно влияющая на передачу энергии по проводам" и работу многих электротехнических устройств. Эти соображения, однако, не ограничивают при- менение переменного тока других частот для решения различных технических и научных задач. Например, частота переменного синусоидального тока элек- трических печей для выплавки тугоплавких металлов составляет до 500Гц.

В радиоэлектронике применяются высокочастотные (мегогерцовые) устрой- ства, так на таких частотах повышается излучение электромагнитных волн.

В зависимости от числа фаз электрические цепи переменного с тока под- разделяются на однофазные и трехфазные.

ЭЛЕКТРИЧЕСКИЕ ЦЕПИ ОДНОФАЗНОГО ТОКА.

Основные характеристики синусоидального переменного тока

Основные величины переменного тока являются функциями времени, назы-

ваются мгновенными значениями и обозначаются строчными буквами e,i и т.д.

Источником переменного тока является соответствующая ЭДС - e (t) , кото-

рая изменяется во времени по закону синуса, т.е.

e (t) = E_m sin (t+) (4.1)

где e (t) - мгновенное значение ЭДС ; Е_m - максимальное значение ЭДС (амплитуда);  - угловая (циклическая) частота измеряемая радиан в секунду (Рад/с); t – время (с) ;  – начальная фаза. Такую ЭДС в дальнейшем будем называть синусоидальной ЭДС.

Её графическое изображение показано на рис. 4.1

Рис.4.1

Период Т – это время за которое происходит полный цикл изменения синусоидального тока или время, за которое рамка генератора совершит один оборот. Период - это величина, обратно пропорциональная частоте T = l / f.

Частота f - это количество полных циклов изменения переменного тока за единицу времени. Единица измерения частоты - Герц. (1 Гц == 1/с);

f = l / T (4.3)

Частота f связана с угловой частотой  выражением: f = 2  

Фазовый угол  = t + . Это угол поворота рамки генератора в данный момент времени или значение аргумента синусоидальной функции, определяющей значение тока. В момент времени t=0 имеем  = . Значение фазового угла при t=0 называется начальным фазовым углом или начальной фазой.

Действующее значение переменного тока I. Это значение введено для измерения величины переменного тока. Оно определяется путем сопоставления теплового действия переменного тока с тепловым действием постоянного тока. Переменный ток i проходя за единицу времени через проводник, нагревает его) т.е. выделяет определенное количество тепла. Можно подобрать постоянный ток такой величины, который за это же время в этом же проводнике выделит такое же количество тепла. Значение постоянного тока I, выделяющего такое же количество тепла за единицу времени как и переменный ток i, называется действующим значением переменного тока I. Действующее значение переменного тока определим, исходя из равенства выделенной тепловой энергии для постоянного и переменного токов за время T

(4.4)

подставляя i == lm Sin 2 wt. получим

(4.5) .

Получение синусоидальной ЭДС осуществляется с помощью генератора переменного тока, работа которого основана на явлении электромагнитной индукции.

Электромагнитной индукцией называется явление возникновения ЭДС в проводнике (контуре) при изменении магнитного потока, сцепляющегося с ним. Рассмотрим принцип действия простейшего генератора переменного тока (рис.4.2).

Рис.4.2

.

Простейший генератор представляет собой рамку с кольцами, посещенную в магнитное поле постоянных магнитов. Если рамку вращать вокруг оси 00', то её стороны аЬ и cd будут пересекать магнитное поле и в этих сторонах согласно закону электромагнитной индукции будет возникать ЭДС.

Направление ЭДС определяется правилом правой руки. "Если правую руку расположить так, чтобы силовые линии магнитного поля входили в ладонь, а отогнутый большой палец показывал направление движения проводника, то четыре вытянутых пальца покажут направление ЭДС."

Простейший генератор представляет собой рамку с кольцами, помещенную в магнитное поле постоянных магнитов. Если рамку вращать вокруг оси ОО’, то ее стороны ab и cd будут пересекать магнитное поле и в этих сторонах согласно закону электромагнитной индукции будут возникать ЭДС е. Направление ЭДС определяется правилом правой руки: если правую руку расположить так , чтобы силовые линии магнитного поля входили в ладонь, а отогнутый большой палец показывал направление движения проводника, то четыре вытянутых пальца покажут направление ЭДС. Величина ЭДС (е) определяется по формуле

е = B L V (4.2)

где В-величина магнитной индукции;

L-длина проводника, равная расстоянию между точками a и b;

V-скорость движения проводника в направлении, перпендикулярном силовым линиям магнитного поля.

При повороте рамки на 180^о направление ЭДС в каждой стороне рамки будет меняться на противоположное. Для получения синусоидального закона изменения ЭДС полюсные наконечники генератора выполняются такой формы, чтобы магнитная индукция В изменялась при повороте рамки по закону синуса.

Представление синусоидальных величин векторами и комплексными числами.

При анализе цепей переменного тока, в которых протекают синусоидальные токи и имеются синусоидальные напряжения, часто возникает необходимость суммирования нескольких величин токов, ЭДС или напряжений одной и той же частоты w, но с различными амплитудами и начальными фазами. При этом

аналитическое и графическое суммирование приводит к определенным трудностям и большим затратам времени. Поэтому целесообразно синусои-

дальную функцию представить в виде вектора или комплексного числа.

Так как синусоидальная функция зависит от двух переменных аргументов: амплитуды и фазового угла (или фазы), то эту синусоидальную функцию можно представить в виде вектора в прямоугольной системе координат X и Y. При этом длина вектора будет равной амплитуде синусоидальной функции, а

его угол наклона по отношению к оси ОХ равен фазовому углу синусоидальной функции.

Рассмотрим выражение для синусоидального тока i=I_msin(t+) Его амплитуда равна I_m , а фазовый угол =(t+). Из этого следует, что фазовый угол  непрерывно изменяется (увеличивается) во времени с угловой скоростью . Поэтому для удобства синусоидальные токи, напряжения, эдс, представляют в виде векторов, рассматривая момент времени t=0. При этом t=0 и =, т.е. фазовый угол равен начальному фазовому углу (рис.4.3).

При изображении синусоидальных токов (напряжений, ЭДС) длину вектора принимают равной действующему значению тока (ЭДС, напряжения).

Рис.4.3.

Вектор тока будем обозначать заглавной буквой с точкой наверху ( i ), аналогично обозначаются векторы других величин.

Известно, что любой вектор может быть представлен в виде комплексного числа, состоящего из вещественной и комплексной части.

при этом вещественная часть численно равна проекции вектора на ось ОХ (вещественная ось), а мнимая часть -проекции вектора на ось OY (мнимая ось).

В этом случае вектор тока можно записать в виде I = a+jb, где а=I_X – веще- ственная часть; Ь=I_Y -мнимая часть.

Таким образом, вектор тока можно представить в виде комплексного числа, т.е. комплексного тока. Комплексное число может быть записано в алгебраической форме:

i = x + j y (4.6)

в тригонометрической форме:

i = A (Cos + j Sin) (4.7)

и в показательной форме:

i = А е ^j (4.8)

Между величинами х, у,  и А существуют следующие зависимости:

А = I; x = A Cos ; у = A Sin ; (4.9)

А = ( х+²у² ) ^1/2;  = arctg (у/х) (4.10)

Величина А = I называется модулем комплексного числа,  - аргумент комплексного числа.

Потенциальная (топографическая) диаграмма

Потенциальная (топографическая) диаграмма показывает распределение комплексных потенциалов точек и напряжений на комплексной плоскости. Она наглядно иллюстрирует работу и параметры сложных цепей переменного тока. На рис.4.4 представлен пример такой диаграммы совмещенной с векторной диаграммой токов.

+j

+1

Рис. 4.4.

ОСНОВНЫЕ ЭЛЕМЕНТЫ ЭЛЕКТРИЧЕСКОЙ ЦЕПИ

СИНУСОИДАЛЬНОГО ТОКА

Линейное активное сопротивление

При прохождении переменного тока через сопротивление происходит вытеснение тока к поверхности проводника, т. е. возникает поверхностный эффект. Эффективная площадь поперечного сечения уменьшается и его сопротивление увеличивается. Таким образом, величина сопротивления постоянному и переменному току не одинакова (для переменного тока она больше и увеличивается с увеличением частоты). Поэтому сопротивление при прохождении через него переменного тока называется не просто сопротивле- нием, а активным сопротивлением и обозначается буквой r.

Сопротивление при прохождении через него постоянного тока обозначается R и называется омическом сопротивлением.

Рис. 4.5.

Пусть через активное сопротивление r протекает синусоидальный ток U(t) = I_mSint. Тогда напряжение U(t) будет тоже иметь синусоидальный характер U(l) = I_mSint. В соответствии с законом Ома:

Обычно закон Ома записывают через действующие значения тока I и напряжения U

r = U / I

Начальные фазы тока и напряжения совпадают. Векторная диаграмма токов и напряжений имеет вид.

Рис.4.6.

Линейный индуктивный элемент

Индуктивный элемент преобразует энергию тока в энергию магнитного поля и может рассматриваться как аккумулятор энергии.

Линейный индуктивный элемент представляет преимущественно обмотку (катушку) в которой собственное потокосцепление пропорционально току.

Его параметром служит индуктивность L, а обозначение на рис. 4.6.

Рис. 4.7.

Пусть через катушку индуктивности L протекает синусоидальный ток i(t) = I_m Sin t. В этом случае падение напряжения U(t) на катушке индуктивности будет определяться величиной ЭДС самоиндукции, т.е.

Закон Ома для амплитуд тока и напряжения имеет вид:

U_m=I_mL; обозначая L= xL , получим

xL = L (4.11)

где, xL - индуктивное сопротивление

Начальная фаза напряжения  = п /2, т.е. вектор напряжения сдвинут по фазе относительно вектора тока на угол 90'. В соответствии с этим векторная диаграмма будет иметь вид

UL

Рис. 4.8.

Линейный емкостной элемент

Емкостной элемент преобразует энергию напряжения электрического тока в энергию электрического поля и может рассматриваться как аккумулятор энергии. Линейный емкостной элемент представляет преимущественно конденсатор в котором значение заряда пропорционально напряжению.

Его параметром служит емкость С , а обозначение на рис. 4.7.

С

Рис. 4.9.

Пусть к емкости С подключено синусоидальное напряжение U(t) = U_mSin t. В результате перемещения зарядов через конденсатор потечет переменный ток i(t) . Величина тока определяется по формуле:

О

тсюда

Переходя от косинуса к синусу, получим

В

водя обозначение

получим:

Определим отношение U_m / I_m = l /C

Хс =l /C (4.12)

Хс - емкостное сопротивление

Вектор тока на конденсаторе опережает вектор напряжения на угол п /2.

Векторная диаграмма

п /2

Рис. 4.10.

Цепь с последовательным соединением элементов r, L, С.

Рис. 4.11.

Пусть i(t) = I_m sint определим падения напряжения на всех элементах этой цепи. По второму закону Кирхгофа получим:

Изобразим векторную диаграмму токов и напряжений

Рис. 4.12.

U_A=I r - активное напряжение; U_P = U_L-U_C - реактивное напряжение

U_L=I x_L; U_C=I x_С (4.13)

(4.14)

Векторная диаграмма сопротивлений

Рис. 4.13.

Х_P = Х_L-Х_C - реактивное; Z - полное сопротивление

Z =  r²+ Х_P² (4.15)

Векторная диаграмма мощностей; коэффициент мощности

Умножим каждую сторону треугольника напряжений на ток I. В результате получим векторная диаграмма мощностей (треугольник) мощностей.

Рис. 4.14.

Здесь: S - полная мощность, P-активная мощность, Q-реактивная мощность.

Полная мощность S - это мощность, вырабатываемая источником электро- энергии. Она состоит из двух составляющих: активной мощности Р и реактивной мощности Q. Причем величина полной мощности определяется по формуле:

(4.16)

Активная мощность Р источника расходуется на выполнение полезной работы (создание вращающего момента, нагрев и т.д.).

Реактивная мощность Q источника расходуется на перемагничивание катушек индуктивности L и перезарядку конденсаторов С. При этом происхо- дит процесс колебания энергии между источником и потребителями L и С.

Коэффициент мощности сos определяет долю активной мощности в полной мощности, вырабатываемой источником сos = Р / S.

Так как Р = S сos , то из этого следует: чем больше величина сos, тем больше мощности источника расходуется на полезную работу, т.е. тем больший кпд энергоустановки. При сos= 1 вся мощность, вырабатываемая источником, расходуется на полезную работу. При малых значениях сos для получения необходимой активной мощности необходимо иметь большое значение полной мощности, что связано с большими потерями электроэнергии, перерасходом металла и т.д. Таким образом коэффициент мощности - cos определяет эффективность выполнения полезной работы.

Резонанс напряжений (при последовательным соединением r, L, С )

При x_L= x_C реактивное сопротивление равно нулю x_P=0 и наступает резонанс напряжений U_L= U_C. При этом :

U_L=U_A , U_P=0 , U=U_A , Z = r , (4.17)

I=U/r = max; cos=1 (4.18)

График изменения напряжения U_L, U_P, U при изменении частоты

0

Рис. 4.15.

Здесь 0 – резонансная частота значения которой определяются по выра- жениям при резонансе Х_L = Х_C учитывая Хс =l /C; ХL = L получим:

l /C = L откуда 0 l / C L (4.19)

Явление резонанса напряжений используется в радиотехнике для выделения частоты передачи и приема радиосигналов за счет I(0) = max;

а в электротехнике для повышения коэффициент мощности - cos так как

cos = 1, т.е. – максимальное значение.

Цепь с параллельным соединением элементов r, L, С.

Рис. 4.16.

В соответствии с первым законом Кирхгофа

I=I_A+ I_L+ I_C

I_A=U/r; I_L=U/L; I_C=UC;

Построим векторную диаграмму токов и напряжения

Рис. 4.17.

(4.20)

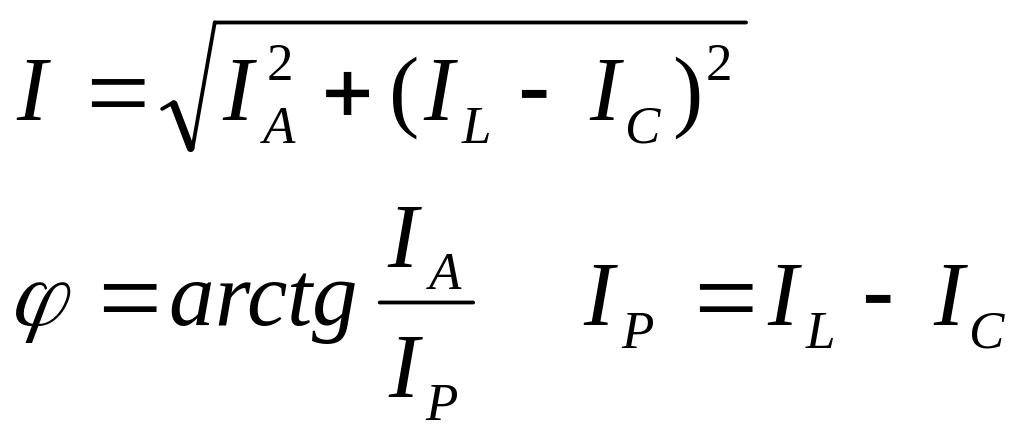
(4.21)

В треугольнике токов разделим каждую сторону на напряжение, в результате получим векторную диаграмму (треугольник) проводимостей.

Рис. 4.18.

g- активная, b = b _L- b _C - реактивная, y - полная проводимости;

g = I_A U; b = I_P U = I_L / U - I_C / U; y = I / U ; y =  g² + b² (4.22)

Векторная диаграмма мощностей

Умножим каждую сторону треугольника токов на напряжение U. В результате получим векторная диаграмма мощностей (треугольник) мощностей.

Рис. 4.19.

Здесь: S - полная мощность, P-активная мощность, Q-реактивная мощность.

Коэффициент мощности сos определяет долю активной мощности в полной мощности, вырабатываемой источником сos = Р / S.

Резонанс токов (при параллельным соединением r, L, C )

При b_L= b_C реактивная проводимость равна нулю b = 0 и наступает резонанс токов I_C = I_L При этом :

I = I_A = U/r = min; cos=1 (4.23)

График изменения токов при изменении частоты

0

Рис. 4.20.

Здесь 0 – резонансная частота значения которой определяются по выра- жениям при резонансе b_L = b_C учитывая bс = C; bL = l /L получим:

C = l /L откуда 0 l / C L (4.24)

Явление резонанса напряжений используется в радиотехнике для создания резонансных фильтров за счет I(0) = min; а в электротехнике для повышения коэффициент мощности - cos так как cos = 1, т.е. – максимальное значение.

ЧАСТОТНЫЕ ХАРАКТЕРИСТИКИ ЦЕПИ

Частотным годографом называется совокупность геометрических мест конца вектора, изображающего комплексную величину, при изменении угловой час- тоты в границах 0< < °° например рис. 4.21а.

Частотной характеристикой называется зависимость модуля вектора изобра-жающего комплексную величину, или его действительной и мнимой состав-ляющих от угловой частоты, например рис. 4.21б.

Рис. 4.21.

где Z = r + j L = Re Z + j Im Z

При этом различают : амплитудно-фазные частотные характеристики (АФЧХ) A(j, амплитудно-частотные характеристики (АЧХ) A(, фазно-частотные характеристики (ФЧХ) ψ(ω).

Лекция 6

МЕТОДЫ РАСЧЕТА ЛИНЕЙНЫХ ЦЕПЕЙ ПЕРЕМЕННОГО ТОКА.

Учитывая специфику представления величин синусоидального тока векторами и комплексными числами соответственно применяются методы: векторных диаграмм и символический).

Метод векторных диаграмм

Данный метод заключается в построении векторных диаграмм и измерении по ним значений искомых величин. Достоинствами этого метода является простота и наглядность, а недостатками трудоемкость, относительно низкая точность. Из-за простоты и наглядности метода он часто применяется в учебных целях, как это видно из ранее рассмотренных векторных диаграмм для последовательного и параллельного соединения элементов r, L, С.

Пример применения метода векторных диаграмм для цепи со смешанным соединением элементов r,L,C:

U(t)

I

I₂

r₃

С

r₂

L₃

Рис. 4.22.

Дано: U,r₁, r₂, r₃, L₁, L₂, C, . Определить: I, I₁, I₂, .

Для построения векторной диаграммы необходимо вначале определить общий ток I. I=U/Z; где Z-полное сопротивление цепи. Оно состоит из сопротивления Z₃ элементов L₃ и г₃ и сопротивления параллельных ветвей Zaб.

Для определения Zab целесообразно определить активную и реактивную проводимости параллельных ветвей. Для этого определим эквивалентные проводимости последовательных элементов в ветвях . Представим ветвь г₁ L_1` эквивалентным параллельным соединением двух проводимостей g₁ и b₁.

Схема 1 . Схема 2.

. Построим векторные диаграммы и соответственные им треугольники сопротивлений для обеих схем, а) для первой схемы б) для второй схем

а).

б).

Так как треугольники сопротивлений и проводимостей подобны (один и тот же угол ₁ ), то имеем:

отсюда и

Учитывая, что y₁=1/Z₁ и Z₁=1/y₁ получим

и

А

налогично, отсюда

отсюда и

Теперь определим эквивалентную проводимость разветвления (участка а)

где

На основании проводимости определяем эквивалентные сопротивления участка аб

где

Теперь можно определить общий ток цепи I

где

Z1 - общее сопротивление цепи.

Чтобы найти токи в параллельных ветвях I₁ и I₂ найдем сначала U_AB

где

После этого определим токи I₁ и I₂

Напряжение на неразветвленном участке цепи

Построение векторной диаграммы производится следующим образом.

В качестве исходного вектора выберем вектор напряжения U_AB По отноше-

нию к нему вектор тока I₁ отстает на угол ₁.Эгот угол легко построить. Для этого вдоль U_AB проведем в масштабе отрезок, равный г₁ и перпендикулярно ему - отрезок, равный X_L1 .Получим прямоугольный треугольник, у которого угол между катетом г₁ и гипотенузой Z₁ равен ₁.

Для определения угла ₂ между вектором напряжения U_AB тока I₁ строим треугольник сопротивлений со стороной г₂, расположенной вдоль U_AB и стороной X_L2, расположенной перпендикулярно к U_AB. Из конца вектора I₁ под углом ₂ проведем вектор I₂. Сумма векторов I₁+I₂ даст вектор тока I.

Для построения вектора напряжения U необходимо вначале построить вектор напряжения U₃. Для этого из конца вектора U_AB проводим вектор U_r3, параллельный вектору тока I. Перпендикулярно вектору U_r3 проводим вектор U_L3. Соединив концы векторов U_AB и U_L3 получим вектор U₃ ( U=U_r3+U_L3 )

Т.к. U=U_AB+ U₃ то для получения вектора U необходимо соединить начало вектора U_AB с концом вектора U₃. Угол  определяется, как угол между векторами I и U.

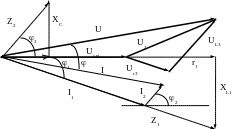
Рис. 4.23

Символический метод.

Символический метод расчета электрических цепей переменного тока осно- ван на представлении величин токов, напряжений, сопротивлений, мощностей в виде комплексных чисел. При этом могут применяться ранее рассмотренные методы: составления уравнений по законам Ома и Кирхгофа, эквивалентных преобразований, контурных токов, метод наложения, узловых потенциалов, эквивалентного источника. Достоинствами символического метода является высокая точность, возможность применения разных численных методов и расчета на компьютере, а недостатками – не наглядность, сложность.

Особенностью расчета цепей с использованием символического метода является то, что при сложении или вычитании комплексных величин их удобнее представлять в алгебраической форме, а при умножении или делении - в показательной.

Для определения активной и реактивной составляющих тока, напряжения, мощности, сопротивления величину удобно представлять в алгебраической форме, а для определения начальной фазы и модуля (действующего значения)- в показательной форме.

Так , если ток изменяется по закону i(t)= I_m*sin(t+_i), то в комплексной форме он будет иметь вид:

для напряжения

Закон Ома в комплексной ( символической форме)

Пример применения символического метода для цепи со смешанным соединением элементов r,L,C:

Рис.4.24

1. Используя законы Ома и Кирхгофа составим систему уравнений, которая

в дифференциальной и символической формах имеет вид:

2. Определим комплексы действующих значений токов методом контурных токов (выбранные положительные направления контурных токов представлены на схеме ).

Решая систему уравнений методом подстановки или определителей находим искомые значения токов i 11, i 22.

Данное решение удобно получить, воспользовавшись машинной программой решения системы алгебраических уравнений с комплексными коэффициентами.

Токи ветвей:

3. Для построения топографической диаграммы за точку отсчета потенциала принимаем узел 5.

Целесообразно идти по каждой из ветвей схемы от точки 5 к точке 1 "навстречу" току. Например при обходе по правой ветви находим потенциалы:

Р

азличие между полученными значениями несущественно. По полученным результатам строим топографическую диаграмму напряжений, совмещенную с векторной диаграммой токов.

+1

Рис. 4.25

4. Определим показание ваттметра. Для этого нужно рассчитать :.

ъ

5. Составим баланс мощности:

Значит, Р_пр = Р_ист, Q_пр = Q_ист и S_пр = S_ист (с погрешностью, определяемой погрешностью расчета).

ЧАСТОТНЫЙ АНАЛИЗ ЦЕПИ

Одним из наиболее распространенных алгоритмов частотного анализа линейных цепей является:

• составление узловых или контурных уравнений электрической цепи для установившегося режима;

• задание значения частотных воздействий;

• определение реакции цепи на воздействие с единичным действующим значением и нулевой начальной фазой ( );

• изменение значения частоты воздействия;

• определение реакций цепи на изменяемые по частоте воздействия.

В результате получается дискретный ряд значений реакции цепи, например , т. е. получается частотная характеристика . Так как _вх(jω) = 1, то отдельные значения этой характеристики численно равны _вых(jω), т.е. , при этом

. (4.7)

Модули этих комплексных значений представляют амплитудно-частотную характеристику А(ω), а аргумент – фазочастотную характеристику ψ(ω). При этом в качестве независимой переменной можно использовать частоту f, циклическую частоту ω, или их относительные значения, выраженные в декадах.

Например, если отсчет частоты начать с 1 Гц, то соответствующая ось частот будет выглядеть (для f_опор=1 Гц) таким образом:

1 10 100 1000 10000 100000 1000000 f (Гц)

0 1 2 3 4 5 6 (дек)

В технической литературе часто f_опор опускают и пишут .

Значения функций амплитудно-частотной характеристики могут быть безразмерны , , или иметь размерность соответствующего параметра, например _вх(ω) в омах, или _вх(ω) в сименсах и т.д.

Безразмерные относительные величины иначе могут быть выражены через логарифмические единицы, например децибелы: , , .

В табл. 1 представлены примеры соответствия этих единиц:

Таблица 1

1000 100 10 1 0,1 0,01 0,001	60 40 20 0 -20 -40 -60

Например, проведем частотный анализ для электрической цепи, схема которой изображена на рис.4.26.

Узловые уравнения имеют вид

В приведенной системе всего 2 узловых уравнения для узлов 1 и 2. Этого достаточно, так как и при система имеет вид:

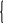
Рис. 4.26

Пусть в первой, второй и четвертой ветвях включены резисторы R₁, R₂, R₄, а в третьей и пятой – емкостные элементы С₃ и С₅, тогда соответствующие проводимости будут равны:

т. е. видно, что параметры цепи частотно-зависимы.

Если обозначить

то уравнение (1.2) преобразуется к виду

Теперь, задаваясь дискретными значениями частоты f, можно, например, определить ряд комплексных значений , т. е. получить ₃(jω). Тогда отношение комплексов выходного и входного напряжений (комплексная передаточная функция) будет при _вх (jω) = 1 численно равна

Здесь _вых(ω) или _вых(f) – амплитудно-частотная характеристика (АЧХ); ψ(ω) или ψ(f) – фазочастотная характеристика(ФЧХ).

Иногда в инженерной практике требуется определить частотную зависимость входного сопротивления или проводимости. Из схемы рис.4.24 нетрудно увидеть, что

Тогда входное сопротивление определится так:

.

Это выражение при примет вид

Если находить дискретно, по точечно для разных значений частоты, получится ряд значений:

Это - частотная характеристика входного сопротивления.

Примеры характеристик полученных в результате частотного анализа приве- дены на рис. 4.27- 4.28.

Рис. 4.27

Рис. 4.28

Лекция 7