Тема1. Элементы линейной алгебры
Литература: 1. Шипачев В.С. Высшая математика. М. Высшая школа. 2008. Гл. 10.
2. Красс М.С. Математика для экономических специальностей. М. Дело. 2002. Гл. 14, 15.
Методические указания.
1. Решение систем трех линейных уравнений с тремя неизвестными методом Крамера.
Система трех линейных уравнений с тремя неизвестными имеет вид
.
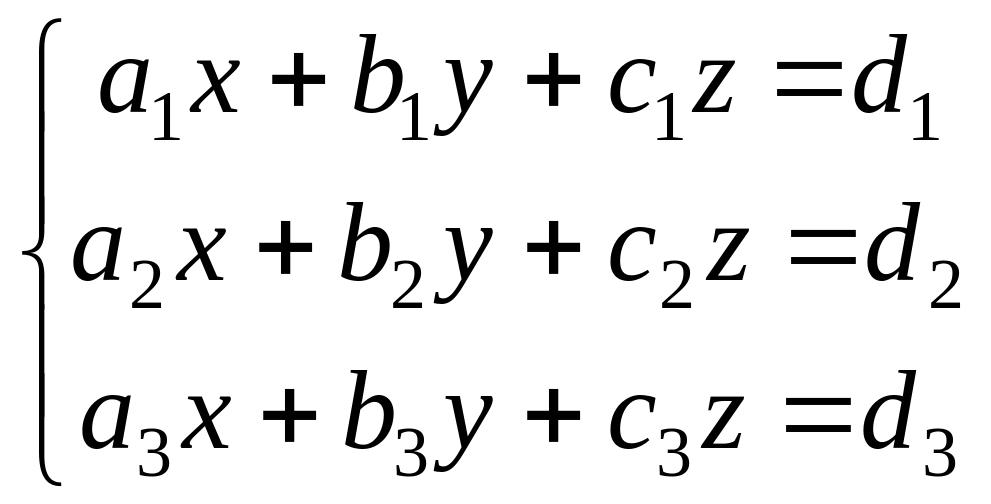(2)
Решением системы (2) называется такая тройка чисел (х;у;z), которая при подстановке в систему обращает каждое уравнение в верное равенство.
Главным определителем системы (2) называется определитель третьего порядка, составленный из коэффициентов при неизвестных:
.
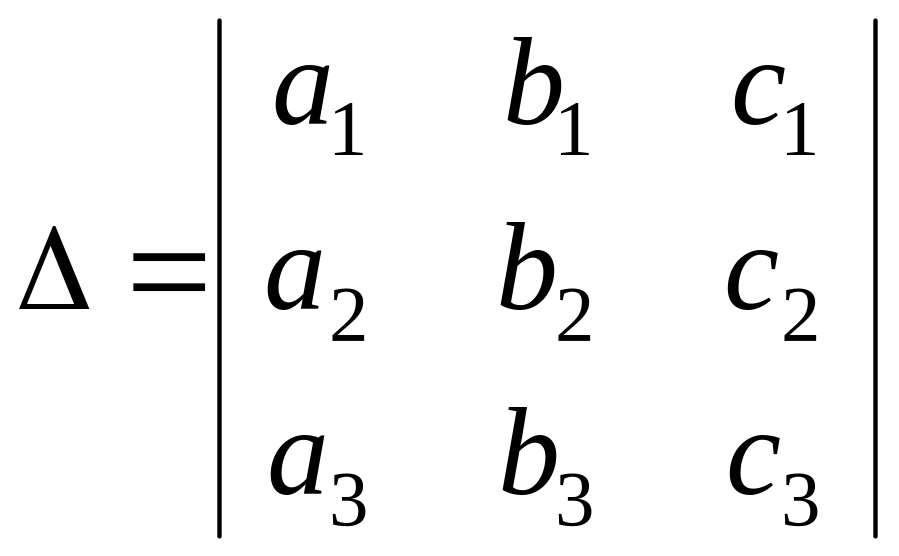Вспомогательные определители системы (2) получаются из главного определителя заменой соответствующего столбца столбцом свободных членов.
;
;
.
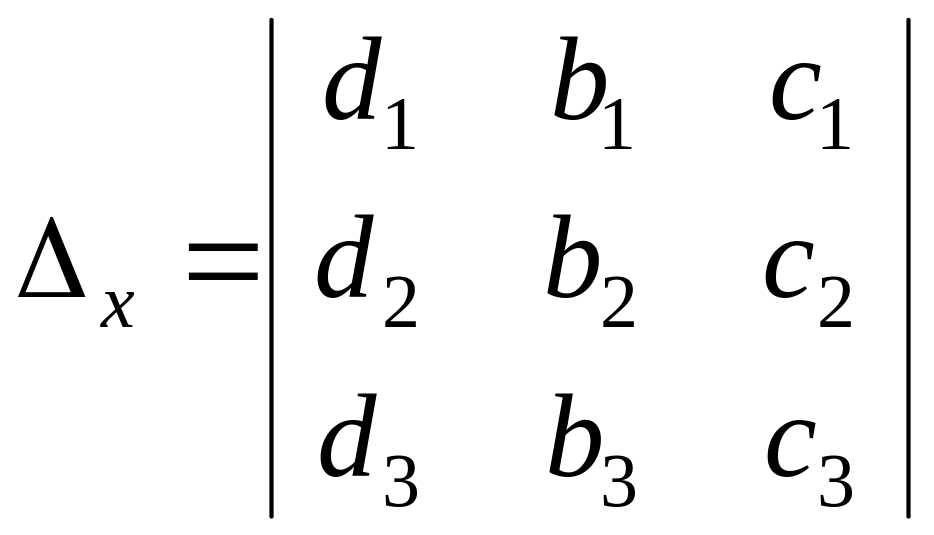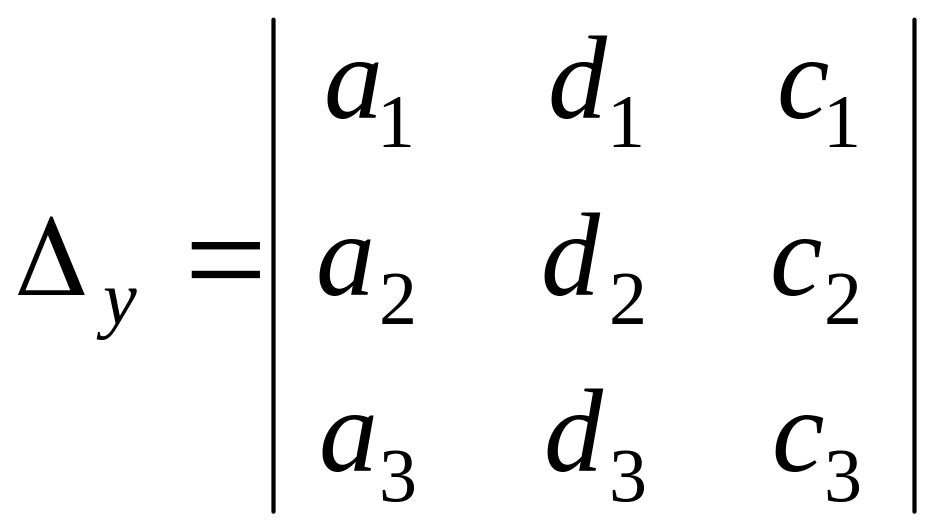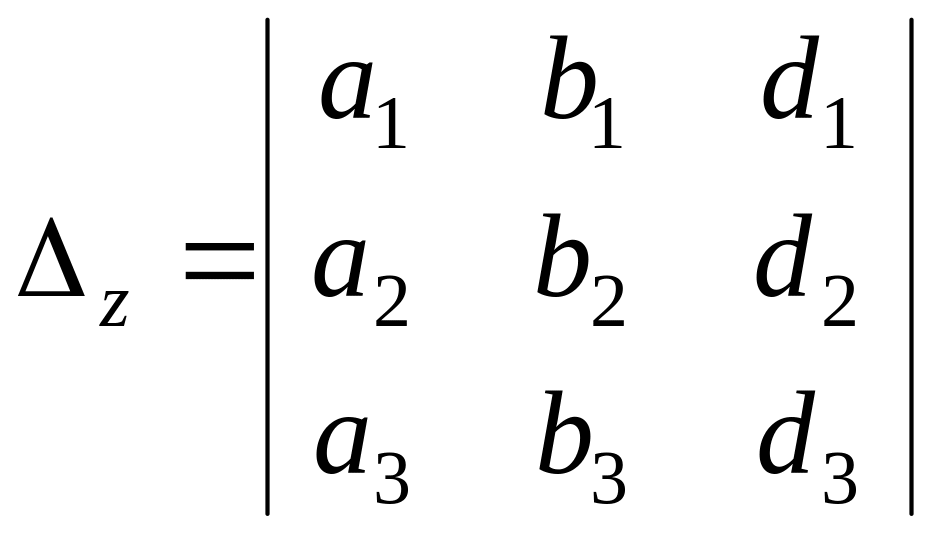Если главный определитель системы не равен нулю, т.е. ∆ ≠ 0, то система (2) имеет единственное решение, которое находится по формулам Крамера:
;
,
.
Если главный определитель системы равен нулю, т.е. ∆ = 0, а хотя бы один из вспомогательных не равен нулю, т.е. ∆х ≠ 0 или ∆у ≠ 0 или ∆z ≠ 0, то система (2) не имеет решений и называется несовместной.
Если главный определитель системы равен нулю, т.е. ∆ = 0, и все вспомогательные равны нулю, т.е. ∆х = 0 и ∆у = 0 и ∆z = 0, то система (2) имеет бесконечное множество решений и называется неопределенной.
Примеры решения задач.
Задача 1. Решить систему
.
Решение.
=
=
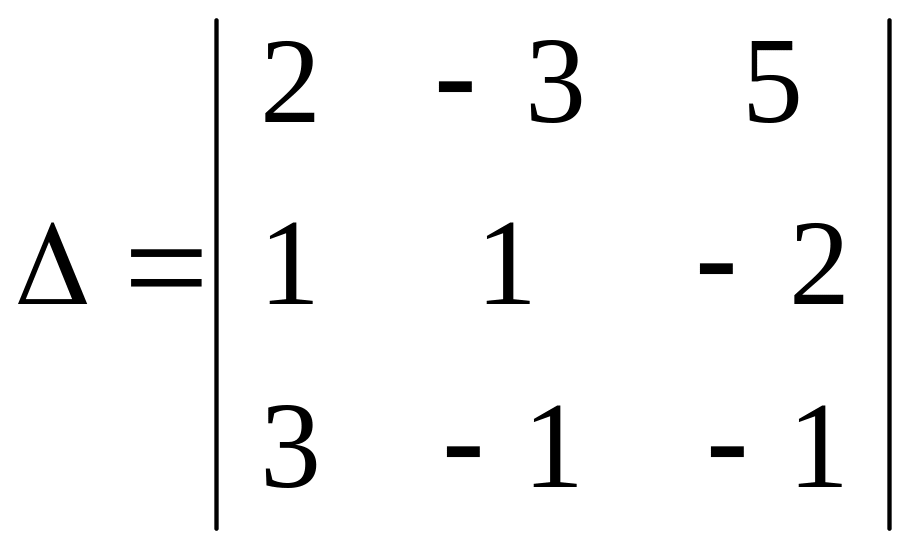= 2(1∙(-1) - (-1)∙(-2)) + 3(1∙(-1) - 3∙(-2)) + 5(1∙(-1) - 3∙1) =
= 2(-1-2) + 3(-1+6) + 5(-1-3) = -6 + 15 - 20 = -11;
=
=
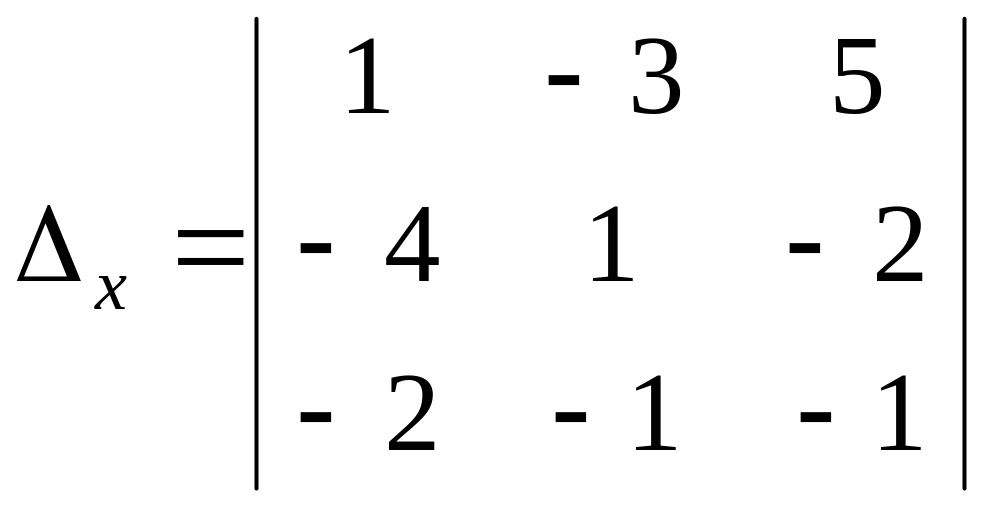= (1∙(-1) - (-1)∙(-2)) + 3((-4)∙(-1) – (-2)∙(-2)) + 5((-4)∙(-1) – (-2)∙1) =
= (-1-2) + 3(4-4) + 5(4+2) = -3 + 0 + 30 = 27.
Аналогично
вычисляются вспомогательные определители
и
:
=45;
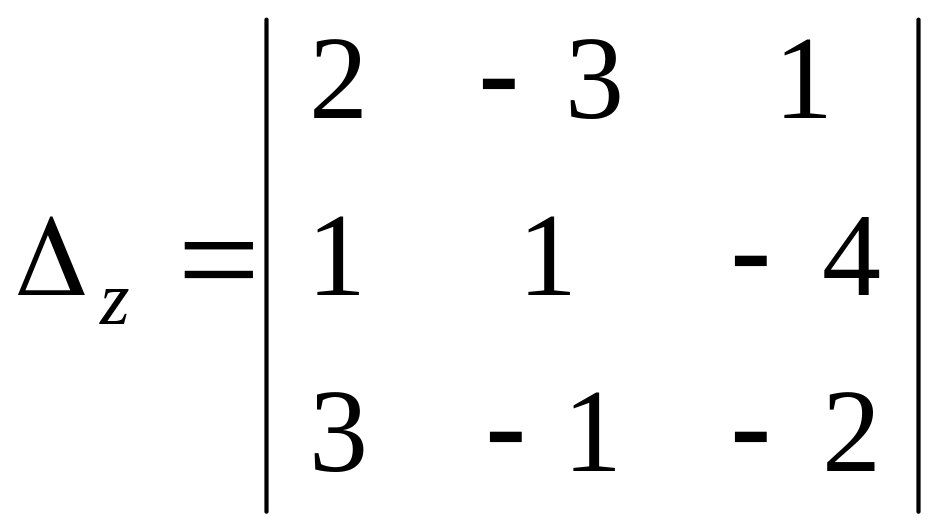= 14.
Так как ∆ ≠ 0, то система имеет единственное решение.
;
,
.
Ответ:
.
2.Решение систем линейных уравнений методом Гаусса.
Система m линейных уравнений с n неизвестными имеет вид:
(1)
Коэффициенты при
неизвестных составляют прямоугольную
матрицу А,
содержащую m
строк и n
столбцов. Если матрица дополнена столбцом
свободных членов, то она называется
расширенной матрицей системы –
.
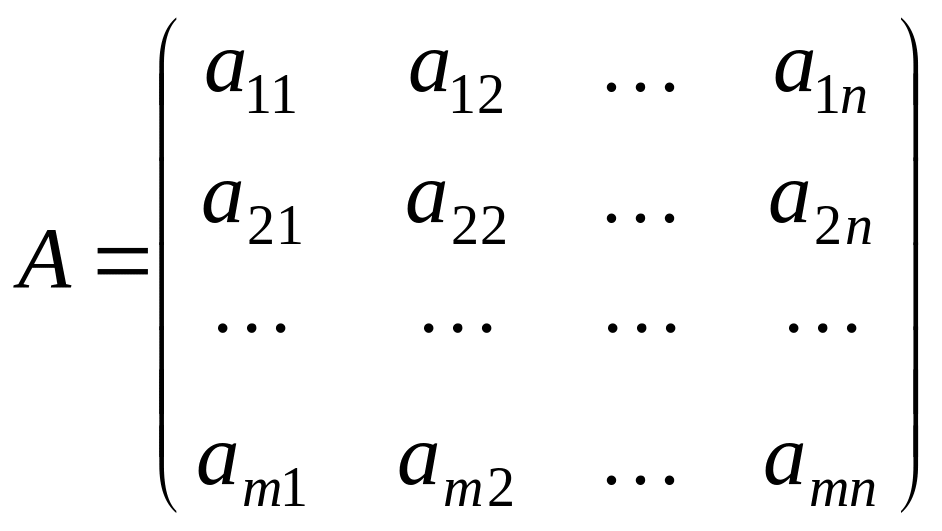
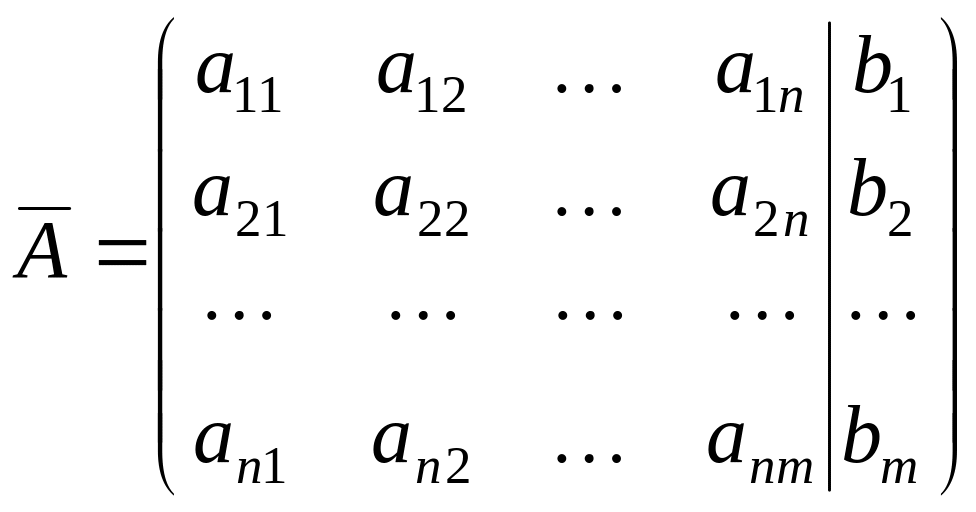
Величины aij называются элементами матрицы, i = 1,2,…m, j = 1,2,…n.
Если m = n, то матрица А называется квадратной. Диагональ матрицы, составленная из элементов a11, a22, … ann называется ее главной диагональю.
Решением системы линейных уравнений (1) называется совокупность n чисел k1, k2, …, kn такая, что при подстановке ее вместо неизвестных каждое из уравнений системы (1) обращается в равенство.
Если система не имеет решений, то она называется несовместной. Если система имеет одно решение, то она называется определенной. Если система линейных уравнений имеет более одного решения, то она называется неопределенной.
Две системы линейных уравнений называются равносильными (эквивалентными), если множества их решений совпадают.
Рассмотрим метод последовательного исключения неизвестных или метод Гаусса решения системы линейных уравнений. С помощью преобразований, которые не нарушают равносильность системы уравнений, а именно:
а) перестановка уравнений в системе;
б) умножение обеих частей любого уравнения на число, отличное от нуля;
в) прибавление к одному уравнению системы другого, умноженного на любое число отличное от нуля, от системы (1) переходят к системам вида:
(2)
или
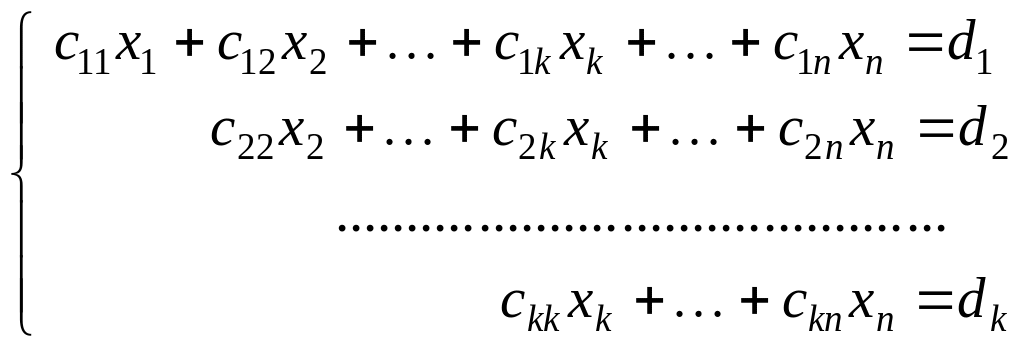(3)
Система (2) называется системой треугольного вида, а система (3) – системой трапецеидального вида.
В системе (2) из последнего уравнения находится хn, затем, подставив его значение в предпоследнее уравнение, находим xn-1. Продолжая далее, найдем, что система (2), а следовательно и система (1) обладает единственным решением.
Если система приведена к виду (3), то переменным xk+1, xk+2, … xn можно придавать произвольные значения и затем решать как систему (2). В этом случае переменные xk+1, xk+2, …, xn называются свободными или независимыми переменными, а переменные x1, x2, …, xn называются связанными или зависимыми переменными.
При решении системы линейных уравнений методом Гаусса для приведения ее к виду (2) или (3) следует выписать расширенную матрицу системы и выполнить над строками матрицы следующие элементарные преобразования:
а) перестановка местами двух строк;
б) умножение элементов некоторой строки на число, отличное от нуля;
в) прибавление к элементам i-ой строки соответствующих элементов j-ой строки, умноженной на любое число.