2.5.2. Среднее арифметическое n случайных величин.

Пусть где Х_i – независимые СВ с математическими ожиданиями и дисперсиями (i= ). Применяя свойства математического ожидания и дисперсии к случайной величине Z , получим: . В частности, если все , , то . Можно показать, что , если

Теорема Чебышева. Если последовательность независимых, одинаково распределенных случайных величин с и (i= ), то для (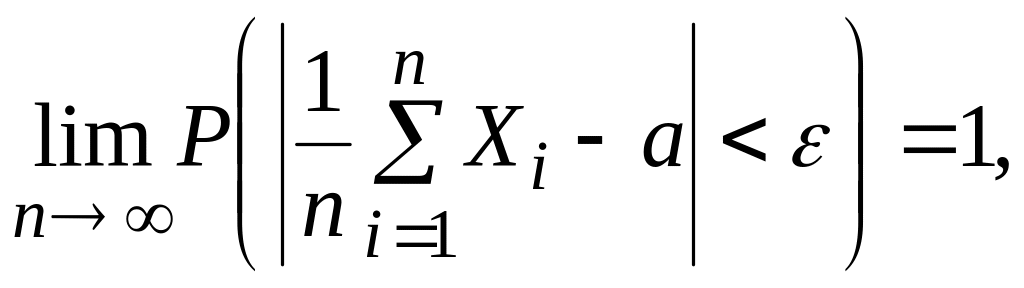краткая запись: ), т.е. сходится к a по вероятности.

Теорема Бернулли. Является частным случаем теоремы Чебышева для схемы Бернулли, в которой каждая случайная величина имеет распределение Бернулли, т. е. принимает значение 1 (с вероятностью p) или 0 (с вероятностью 1–p). Тогда – частость.

Обе теоремы определяют так называемый закон больших чисел. На них основана вся математическая статистика.

2.5.3. Центральная предельная теорема Ляпунова.

Пусть последовательность независимых случайных величин с (i= ), причем ни одна из них не оказывает существенного влияния на их сумму. Тогда распределение СВ при n   приближается к нормальному, а распределение 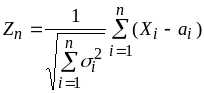сходится к .

Эта теорема объясняет, почему случайные величины часто имеют нормальное распределение. На практике замечено, что если имеют разные распределения, но дисперсии не сильно отличаются друг от друга, то при числе слагаемых n>10 распределение суммы часто можно заменить нормальным.

2.5.4. Распределение Пирсона

Пусть читается: «хи-квадрат»), где независимые СВ, при Распределение этой случайной величины называется распределением Пирсона (или распределением ²) с n степенями свободы. Плотность распределения СВ ² имеет вид:

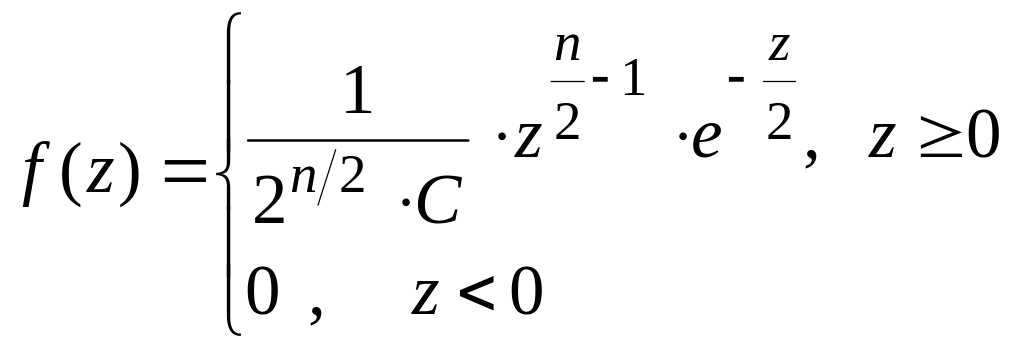
где С = Г – значение гамма-функции Г(х) в точке n/2, Г(х) –табулированная гамма-функция. В частности, если х – целое число, то Г(х)= х! На рис.10 изображены плотности вероятности при n=2 и n=6.

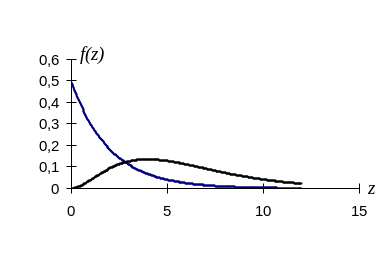
Рис10. Плотность распределения величины ²

При n=2 f(z) –функция монотонная. Математическое ожидание МZ=n, дисперсия DZ=2n.

Распределение Пирсона (оно, как видно из формулы, – однопараметрическое) является частным случаем двухпараметрического гамма-распределения, часто используемого на практике, когда СВ не может принимать отрицательные значения.

В табл.3П приложения содержатся квантили плотности распределения случайной величины для различных значений степени свободы n≡k и различных значений вероятности р т.е. такие значения , при которых справедливо равенство .

5. Распределение Стьюдента.

Пусть где X и независимы, .

Распределение этой случайной величины называется распределением Стьюдента (или Т-распределением) с n степенями свободы.

Плотность распределения Стьюдента имеет вид (рис. 11):

,

где a_n = Г , b_n = Г , Г(х) – гамма-функция.

Рис.11. Плотность распределения Стьюдента

Математическое ожидание, коэффициент асимметрии и коэффициент эксцесса случайной величины Z равны 0, дисперсия DZ= при n>2. Из этого следует, что распределение Стьюдента имеет чуть больший разброс по сравнению со стандартным нормальным N(0;1). При n   f_n (z) сходится к нормальному с математическим ожиданием а=0 и дисперсией .

В табл.2П приложения содержатся квантили t_p плотности распределения случайной величины T(n) для различных значений степени свободы n ≡ k и различных значений вероятности р , т.е. такие значения t_p, при которых справедливо равенство .