2.4. Экспериментальное определение начального напряжения сдвига

Ротационные приборы не могут определить величину начального напряжения сдвига, т. к. невозможно измерять τ при . Часто за величину начального напряжения сдвига принимают либо величину τ при начальном значении , либо экстраполируют ход зависимости до и значение τ, отсекаемое при , принимают за величину начального напряжения сдвига.

Для точного определения величины начального напряжения сдвига должен быть использован другой прибор. Например, U–образная трубка (рис. 2.2). В трубку помещают ВУТ, а затем с одной стороны в нее наливают воду до тех пор, пока суспензия под тяжестью столба воды не начнет двигаться.

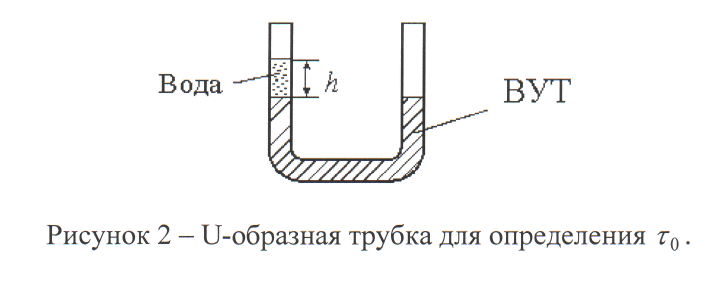
Рис. 2.2. U-образная трубка для определения τ₀ .

Измерив h, при котором суспензия начинает двигаться, определяют τ₀ из равенства давления на границе раздела двух жидкостей

, (2.6)

где – плотность воды; – высота столба воды; D – диаметр трубки; L – длина трубки, занятая ВУТ.

3. Структура и содержание пояснительной записки самостоятельнОй работы

3.1. Построение реологической модели

Пусть проведено измерение на ротационном вискозиметре величины напряжения сдвига в зависимости от скорости сдвига , где m – число скоростей сдвига.

Если известно, что реологическая зависимость имеет вид

, (3.1)

то, согласно методу наименьших квадратов, неизвестные параметры (р – число неизвестных параметров) выбираются таким образом, чтобы сумма отклонений измеренных значений , от их значений, вычисленных по формуле (3.1), была минимальной, т.е.

(3.2)

На основании необходимого условия экстремума функции приравниваем к нулю её частные производные:

(3.3)

В результате получим p+1 уравнений для определения р+1 неизвестных

(3.4)

Решив систему (3.4), получим необходимые значения параметров для построения реологической модели (3.1). Система уравнений (3.4) называется системой нормальных уравнений.

Так для модели Шведова-Бингама (2.4) получим следующую систему нормальных уравнений:

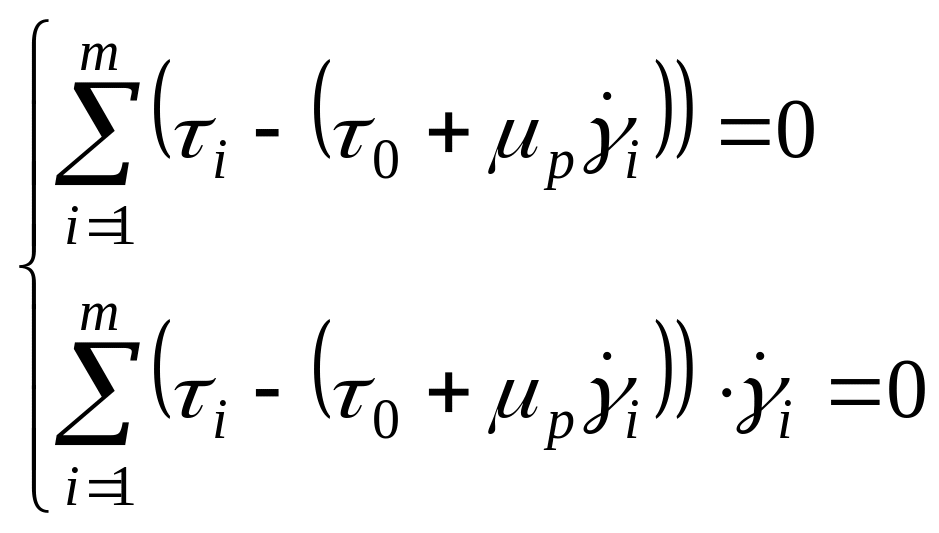(3.5)

После преобразований получим линейную систему двух уравнений с двумя неизвестными:

(3.6)

Решив систему (3.6), получим искомые параметры.

Так как модель Оствальда (2.5) нелинейная, то сводим её к линейной путем соответствующей замены переменных. Логарифмируя (2.5), получим

.

Введя новые переменные

и новый параметр , получим линейную модель

. (3.7)

Определив параметры модели, решая систему (3.4) для зависимости (3.7), можно вернуться к исходной модели (2.5), учитывая, что .

Для оценки соответствия аналитической модели экспериментальным точкам используют среднеквадратичное отклонение

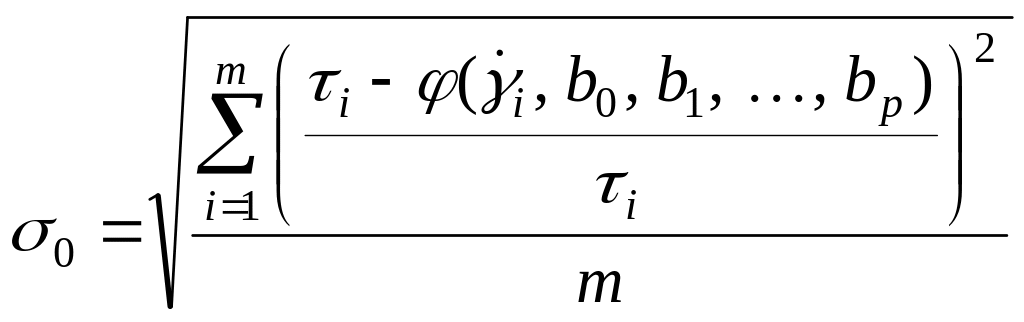. (3.8)

Чем меньше показатель , тем лучше модель описывает экспериментальные значения.