Контрольные вопросы и задания:

1. Какой метод наблюдения целесообразно использовать, если изучается работа леспромхозов в регионах, где лесопромышленный комплекс и целлюлозно-бумажная промышленность составляют не менее 5% общего объема производства в регионе?

2. Что такое единица отбора?

3. Решение каких вопросов зависит от объема выборки? Как влияет объем выборки на ее ошибку?

4. Как определить объем выборки, если не известна генеральная дисперсия?

5. По данным прошлых обследований известно, что доля бездетных семей в городе N составляла 5%. Вычислите объем выборки, обеспечивающий относительную ошибку не более 1% с вероятностью 0,954.

1.7 Статистический анализ связей

В жизни все явления взаимосвязаны. Обычно нас интересуют непосредственные факторы, измерение их воздействия на результат, а также ранжирование факторов по интенсивности их влияния. Особенность связей в экономике и социальной сфере состоит в том, что их закономерный характер проявляется лишь в массе явлений - в среднем по совокупности. Такого рода связи называют статистическими. Они проявляются в том, что при изменении значения фактора изменяется распределение результативного признака. Изменяются и условные средние значения результата (таблица 1.9).

Таблица 1.9 - Проявление статистической и корреляционной связи

Значения фактора	Количество единиц в группе	Распределение значений результата	Средние значения результата
х1	k	y11 y12 …y1k
х2	m	y21 y22 …y2k
х3	p	y31 y32 …y3k

При статистической связи разным значениям одной переменной (фактора, х) соответствуют разные распределения другой переменной (результата, у).

Корреляционная связь - частный случай статистической связи, при котором разным значениям переменной соответствуют разные средние значения другой переменной.

Корреляционная связь предполагает, что изучаемые переменные имеют количественное выражение.

Статистическая связь - более широкое понятие, она не включает ограничений на уровень измерения переменных. Переменные, связь между которыми изучается, могут быть как количественными, так и неколичественными.

Если изучается связь между двумя признаками, налицо парная корреляция. Если изучается связь между многими признаками - множественная корреляция.

Парная корреляция - это изучение корреляционной связи между двумя переменными.

Прежде всего, чтобы проверить, как проявляется связь между двумя переменными, нужно построить график-поле корреляции.

Поле корреляции - это поле точек, на котором каждая точка соответствует единице совокупности; ее координаты определяются значениями признаков х и у.

По характеру расположения точек на поле корреляции делают вывод о наличии или отсутствии связи, о характере связи (линейная или нелинейная, а если связь линейная-то прямая или обратная).

В случае если точки корреляционного поля обнаруживают определенную направленность в своем расположении, можно говорить о наличии связи. При этом корреляционное поле можно оконтурить эллипсом (корреляционный эллипс).

Важнейшей задачей является определение формы связи с последующим расчетом параметров уравнения, или, иначе, нахождение уравнения связи (уравнения регрессии).

Если изучается связь между двумя переменными, причем их можно рассматривать как фактор и результат, т.е. вероятно наличие зависимости, то эту зависимость целесообразно представить в математическом виде. С этой целью подбирают функцию у =f(х), которая наилучшим образом соответствует исходным данным, иначе говоря, обеспечивает наилучшую аппроксимацию поля корреляции. При выборе типа функции руководствуются характером расположения точек на поле корреляции, а также содержанием изучаемой связи. Так, например, при изучении зависимости себестоимости единицы продукции (у) от объема производства (х) теоретический анализ показывает, что такая зависимость должна описываться уравнением гиперболы: , поскольку при увеличении объема производства себестоимость снижается до определенного предела, по достижении которого ее дальнейшего снижения не происходит.

Математически описание зависимости в среднем изменений переменной у от переменной х называется уравнением парной регрессии.

Чаще всего используется линейное уравнение парной регрессии:

, (1.46)

где - среднее значение результативного признака при определенном значении факторного признака х; а - свободный член уравнения регрессии; b - коэффициент регрессии, который показывает, на сколько единиц в среднем изменится результативный признак при изменении факторного признака на одну единицу его измерения.

При такой интерпретации коэффициента регрессии предполагается, что сила воздействия х на у постоянна при любых значениях х.

Знак при коэффициенте регрессии соответствует направлению зависимости у от х:

b>0 - зависимость прямая;

b < 0 - зависимость обратная.

Если в исходных данных имеется нулевое значение х, то свободный член а показывает среднее значение у при х=0.

Во всех остальных случаях а - доводка, обеспечивающая равенство:

. (1.46)

В этом случае значение а не интерпретируется. Знак при свободном члене а зависит от соотношения между интенсивностью вариации (ν) переменных х и у:

если ν _у > ν _х, то а < 0;

если ν _у< ν _х, то а > 0,

где а и b-параметры уравнения парной регрессии.

Если необходимо отразить нелинейность зависимости у от х, то могут быть использованы следующие уравнения регрессии:

, (1.47)

, (1.48)

, (1.49)

и т.д. (1.50)

Выбираемые функции должны быть линейны по параметрам. Перечисленные регрессии приводятся к линейному виду (линеаризуются) путем замены переменных или логарифмирования.

Параметры линейного уравнения парной регрессии находятся методом наименьших квадратов (МНК). Исходное условие МНК формулируется следующим образом:

, (1.51)

т.е. должна быть обеспечена минимальность суммы квадратов отклонений фактических, значений результативной переменной от ее теоретических значений, получаемых на основе уравнения регрессии.

Для отыскания значений параметров а и b, при которых f(а,b) принимает минимальное значение, приравниваем нулю первые частные производные функции:

, (1.52)

(1.53)

Преобразуя полученные уравнения, получаем систему нормальных уравнений МНК для прямой:

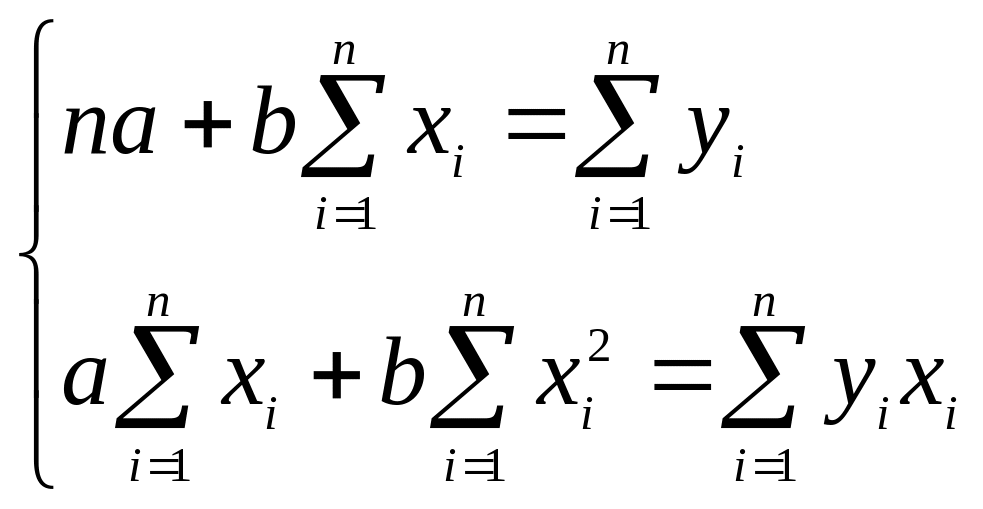(1.54)

Отсюда:

, (1.55)

где Δ - определитель системы; Δ_a - частный определитель, получаемый путем замены коэффициентов при а членами правой части системы уравнений; Δ_b - частный определитель, получаемый путем замены коэффициентов при b членами правой части системы уравнений.

. (1.56)

Тогда

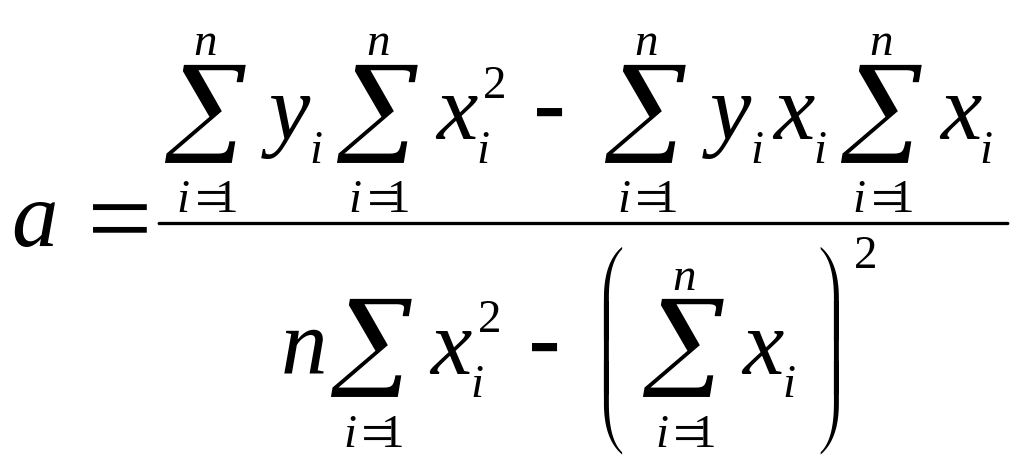; (1.57)

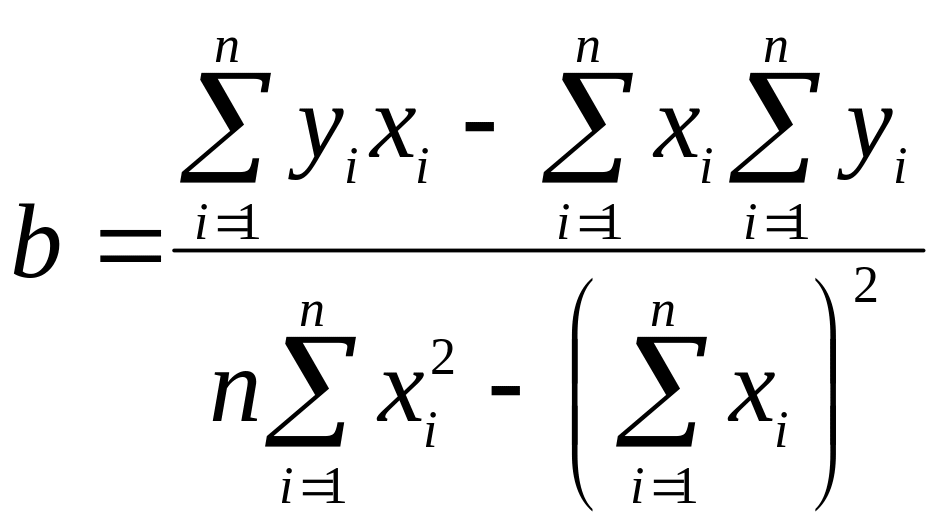. (1.58)

Можно найти параметр а, разделив на n первое уравнение системы:

, (1.59)

отсюда

. (1.60)

Параметр b может быть выражен следующим образом:

. (1.61)

Так как знаменатель этого выражения есть не что иное, как дисперсия переменной х, формула коэффициента регрессии b может быть записана следующим образом:

. (1.62)

Для определения степени тесноты парной линейной зависимости служит линейный коэффициент корреляции r, для расчета которого можно использовать, например, две следующие формулы:

Отклонения от средних по одной и другой переменным лежат в основе измерения корреляционной связи. В случае линейной связи ее теснота измеряется с помощью коэффициента парной корреляции:

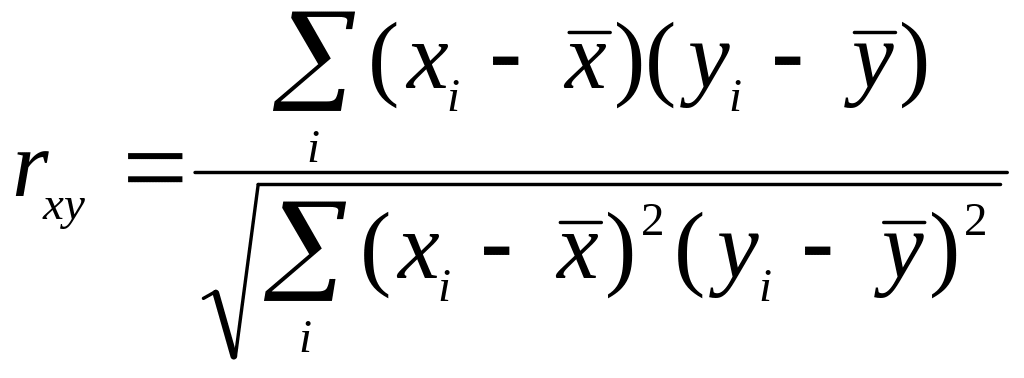. (1.63)

Если знаки отклонений от средних совпадают, то связь прямая (r_xy > 0), если знаки отклонений не совпадают, то связь обратная (r_xy < 0). Разделив числитель и знаменатель на n (число наблюдений), получим:

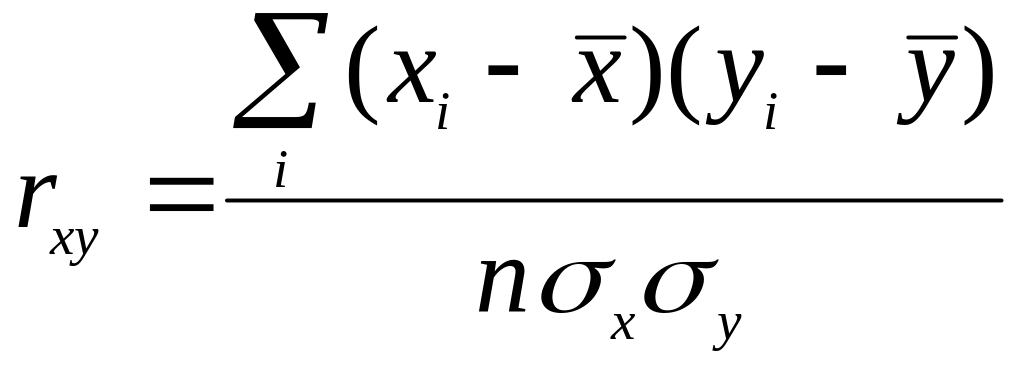(1.64)

или

. (1.65)

Коэффициент парной корреляции измеряется от -1 (случай полной обратной связи) до 1 (случай полной прямой связи). По абсолютной величине: 0≤|r_xy|≤1. Чем ближе значение r_ху к единице, тем теснее связь, чем ближе значение r_ху к нулю, тем слабее связь.

При |r_xy|<0,30 связь считается слабой, при |r_xy| = 0,3 - 0,7 - средней, при |r_xy|>0,7-сильной, или тесной.

Коэффициент корреляции - симметричная мера связи, т.е. это мера взаимосвязи между х и у. Поэтому r_ху = r_ух.

Квадрат коэффициента корреляции представляет собой коэффициент детерминации:

Коэффициент детерминации = r².

Коэффициент детерминации часто более предпочтителен для измерения связи, так как он может быть использован для измерения не только линейных, но и нелинейных связей. Коэффициент детерминации может быть выражен в процентах. Коэффициент детерминации принимает значения в интервале [0, 1]. Чем ближе значение к 1, тем теснее связь, и наоборот.

Коэффициент регрессии можно найти на основе коэффициента корреляции. Поскольку

, , (1.66)

то

. (1.67)

В отличие от коэффициента корреляции коэффициент регрессии является асимметричной характеристикой связи: он характеризует не просто связь между переменными, а зависимость изменения у от х, но не наоборот, т.е. b_ух ≠ b_ху.

Коэффициент детерминации рассчитывается по формуле:

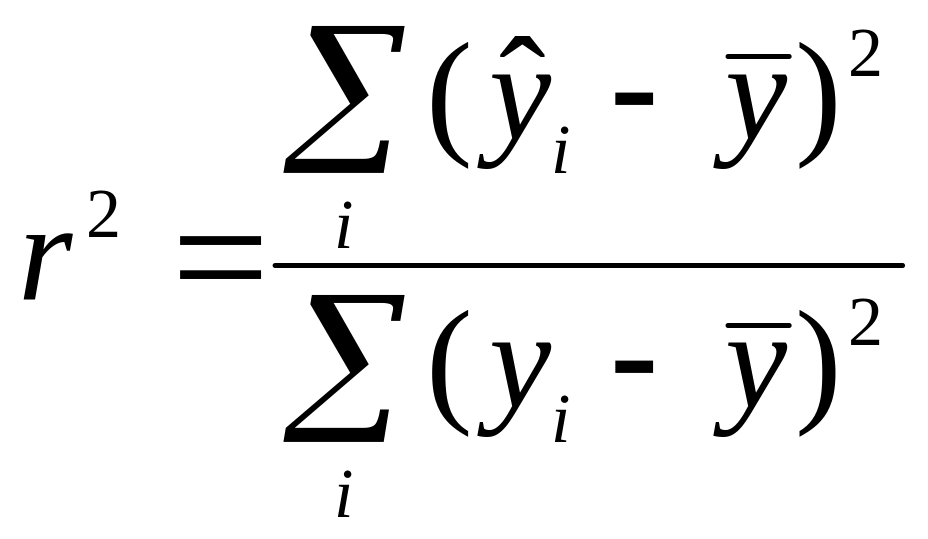. (1.68)