6 Билет Распределение по вектору скорости
Учитывая,
что плотность распределения по
скоростям 
пропорциональна
плотности распределения по импульсам:
и
используя 
мы
получим:
,
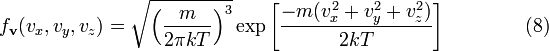что
является распределением Максвелла по
скоростям. Вероятность обнаружения
частицы в бесконечно малом элементе 
около
скорости 
равна
Распределение по проекции скорости
Распределение
Максвелла для вектора скорости 
—
является произведением распределений
для каждого из трех направлений:
,
где распределение по одному направлению:
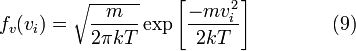
Это распределение имеет форму нормального распределения. Как и следует ожидать для покоящегося газа, средняя скорость в любом направлении равна нулю.
Распределение по модулю скоростей
Обычно, более интересно распределение по абсолютному значению, а не по проекциям скоростей молекул. Модуль скорости, v определяется как:
поэтому
модуль скорости всегда будет больше
или равен нулю. Так как все 
распределены
нормально,
то 
будет
иметь хи-квадрат
распределение с
тремя степенями свободы. Если 
— функция
плотности вероятности для
модуля скорости, то:
,
где
таким образом, функция плотности вероятности для модуля скорости равна
Опыт Штерна — опыт, впервые проведённый немецким физиком Отто Штерном в 1920 году. Опыт явился одним из первых практических доказательств состоятельности молекулярно-кинетической теории строения вещества. В нём были непосредственно измерены скорости теплового движения молекул и подтверждено наличие распределения молекул газов по скоростям.
Для проведения опыта Штерном был подготовлен прибор, состоящий из двух цилиндров разного радиуса, ось которых совпадала и на ней располагалась платиновая проволока с нанесённым слоем серебра. В пространстве внутри цилиндров посредством непрерывной откачки воздуха поддерживалось достаточно низкое давление. При пропускании электрического тока через проволоку достигалась температура плавления серебра, из-за чего атомы начинали испаряться и летели к внутренней поверхности малого цилиндра равномерно и прямолинейно со скоростью v, соответствующей подаваемому на концы нити напряжению. Во внутреннем цилиндре была проделана узкая щель, через которую атомы могли беспрепятственно пролетать далее. Стенки цилиндров специально охлаждались, что способствовало оседанию попадающих на них атомов. В таком состоянии на внутренней поверхности большого цилиндра образовывалась достаточно чёткая узкая полоса серебряного налёта, расположенная прямо напротив щели малого цилиндра. Затем всю систему начинали вращать с некой достаточно большой угловой скоростью ω. При этом полоса налёта смещалась в сторону, противоположную направлению вращения, и теряла чёткость. Измерив смещение sнаиболее тёмной части полосы от её положения, когда система покоилась, Штерн определил время полёта, через которое нашёл скорость движения молекул:
,
где s — смещение полосы, l — расстояние между цилиндрами, а u — скорость движения точек внешнего цилиндра.
Найденная таким образом скорость движения атомов серебра совпала со скоростью, рассчитанной по законам молекулярно-кинетической теории, а тот факт, что получившаяся полоска была размытой, свидетельствовал в пользу того, что скорости атомов различны и распределены по некоторому закону — закону распределения Максвелла: атомы, двигавшиеся быстрее, смещались относительно полосы, полученной в состоянии покоя, на меньшие расстояния, чем те, которые двигались медленнее.
Теорема Гаусса (закон Гаусса) — один из основных законов электродинамики, входит в систему уравнений Максвелла. Выражает связь (а именно равенство с точностью до постоянного коэффициента) между потоком напряжённости электрического поля сквозь замкнутую поверхность и зарядом в объёме, ограниченном этой поверхностью. Применяется отдельно для вычисления электростатических полей.
Аналогичная теорема, также входящая в число уравнений Максвелла, существует и для магнитного поля (см. ниже).
Также теорема Гаусса верна для любых полей, для которых верен закон Кулона или его аналог (например, для ньютоновской гравитации). При этом она является, как принято считать, более фундаментальной, так как позволяет в частности вывести степень расстояния[1] в законе Кулона «из первых принципов», а не постулировать ее (или не находить эмпирически).
В этом можно видеть фундаментальное значение теоремы Гаусса (закона Гаусса) в теоретической физике.
Существуют аналоги (обобщения) теоремы Гаусса и для более сложных полевых теорий, чем электродинамика.
Общая формулировка: Поток вектора напряжённости электрического поля через любую произвольно выбранную замкнутую поверхность пропорционален заключённому внутри этой поверхности электрическому заряду.
СГС |
СИ |
|
|
где
—
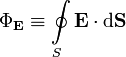поток
вектора напряжённости электрического
поля через замкнутую поверхность
.
—
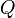полный
заряд, содержащийся в объёме, который
ограничивает поверхность
.
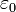— электрическая
постоянная.
Данное выражение представляет собой теорему Гаусса в интегральной форме.
Замечание: поток вектора напряжённости через поверхность не зависит от распределения заряда (расположения зарядов) внутри поверхности.
В дифференциальной форме теорема Гаусса выражается следующим образом:
СГС |
СИ |
|
|
Здесь 
—
объёмная плотность заряда (в случае
присутствия среды — суммарная
плотность свободных и связанных зарядов),
а 
— оператор
набла.
Теорема Гаусса может быть доказана как теорема в электростатике исходя из закона Кулона (см. ниже). Формула однако также верна в электродинамике, хотя в ней она чаще всего не выступает в качестве доказываемой теоремы, а выступает в качестве постулируемого уравнения (в этом смысле и контексте ее логичнее называть законом Гаусса.
Закон Больцмана для распределения частиц идеального газа во внешнем потенциальном поле. n=n0exp(-ep/(kT)) Больцман доказал, что это распределение справедливо не только в случае потенциальных сил земного тяготения, но и в любом потенциальном поле сил совокупности любых одинаковых частиц, находящихся в состоянии хаотического движения. В соответствии с этим это распределение было названо законом Больцмана для распределения частиц идеального газа во внешнем потенциальном поле.
Распределения Больцмана. Основное уравнение МКТ и максвелские распределения молекул по скорости были получены предположением, что молекулы равномерно распределены по объему и все направления движения молекул равномерно распределены по объему и все направления движения молекул равновероятны. Такие условия могут быть реализованы только в том случае, если на молекулы не действуют никакие внешние силовые поля. Однако молекулы любого газа в земных условиях находятся в потенциальном гравитационном поле Земли, что приводит к нарушению равномерного распределения молекул по объему. P = pgh — давление в жидкости ; dP = - pgdh — т.к. с увеличением высоты давление уменьшается.
PV = mRT / μ => p = m / V = Pμ / RT ; dP = - Pμ g dh / RT = P m0 g dh / kT ; dP/ P = - m0 g dh / kT ; Проинтегрируем это выражение:
(интеграл P0 - P) dP / P = - (m0 g / kT) (интеграл 0 - h) dh ; ln (P / P0) = - (m0 gh / kT) ; P = R0 e (ст. m0 gh / kT) ; P = P0 e (ст. — μ n / RT) ; Это выражение описывает распределение частиц по высоте в гравитационном поле. m0 gh = Wп, поэтому n = n0 e (ст. — Wп / kT). Это и есть распределения Больцмана. Оно описывает распределение частиц по высоте в гравитационном поле, а не только в гравитационном поле Земли. Это распределение приемлемо к частицам, находящимся в состоянии заотического теплового движения.
Возьмем
контур l (рис.
2.8), охватывающий прямой ток I,
и вычислим для него циркуляцию вектора
магнитной индукции 
,
т.е. 
.
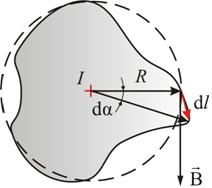
Рис. 2.8
Вначале рассмотрим случай, когда контур лежит в плоскости перпендикулярно потоку (ток I направлен за чертеж). В каждой точке контура вектор направлен по касательной к окружности, проходящей через эту точку (линии прямого тока – окружности).
Воспользуемся свойствами скалярного произведения векторов.
где 
–
проекция dl на
вектор
,
но 
,
где R –
расстояние от прямой тока I до
dl.
.
Отсюда
|
|
(2.6.1) |
|
,это теорема о циркуляции вектора : циркуляция вектора магнитной индукции равна току, охваченному контуром, умноженному на магнитную постоянную.
Иначе обстоит дело, если ток не охватывается контуром (рис. 2.9).
При
обходе радиальная прямая поворачивается
сначала в одном направлении (1–2), а потом
в другом (2–1). Поэтому 
,
и следовательно
|
|
(2.6.2) |
|
,
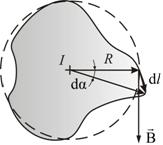
Рис. 2.9
Итак,
,
где I –
ток, охваченный контуром L.
Эта формула справедлива и для тока произвольной формы, и для контура произвольной формы.
Если контур охватывает несколько токов, то
|
|
(2.6.3) |
|
,т.е. циркуляция вектора равна алгебраической сумме токов, охваченных контуром произвольной формы.
Теорема
о циркуляции вектора индукции магнитного
поля 
позволяет
легко рассчитать величину В от
бесконечного проводника с током (рис.
2.10): 
.
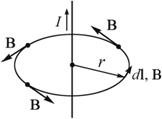
Рис. 2.10
Итак,
циркуляция вектора магнитной
индукции
отлична
от нуля, если контур охватывает ток
(сравните с циркуляцией вектора 
: 
).
Такие поля, называются вихревыми или соленоидальными.
Магнитному
полю нельзя приписывать потенциал, как
электрическому полю. Этот потенциал не
был бы однозначным: после каждого обхода
по контуру он получал бы приращение 
.
Линии напряженности электрического поля начинаются и заканчиваются на зарядах. А магнитных зарядов в природе нет. Опыт показывает, что линии всегда замкнуты (см. рис. 1.2. и 1.7). Поэтому теорема Гаусса для вектора магнитной индукции записывается так:
.
Магни́тная
инду́кция 
— векторная величина,
являющаяся силовой характеристикой магнитного
поля (его
действия на заряженные частицы) в данной
точке пространства. Определяет, с
какой силой 
магнитное
поле действует на заряд 
,
движущийся со скоростью 
.
Более
конкретно,
—
это такой вектор, что сила
Лоренца
,
действующая со стороны магнитного
поля[1] на
заряд
,
движущийся со скоростью 
,
равна
где косым крестом обозначено векторное произведение, α — угол между векторами скорости и магнитной индукции (направление вектора перпендикулярно им обоим и направлено по правилу буравчика).
Также магнитная индукция может быть определена[2] как отношение максимального механического момента сил, действующих на рамку с током, помещенную в однородное поле, к произведению силы тока в рамке на её площадь.
Является основной фундаментальной характеристикой магнитного поля, аналогичной вектору напряжённости электрического поля.
В системе СГС магнитная индукция поля измеряется в гауссах (Гс), в системе СИ — в теслах (Тл)
1 Тл = 104 Гс
Магнитометры, применяемые для измерения магнитной индукции, называют тесламетрами.
Поскольку вектор магнитной индукции является одной из основных фундаментальных физических величин в теории электромагнетизма, он входит в огромное множество уравнений, иногда непосредственно, иногда через связанную с ним напряженность магнитного поля. По сути, единственная область в классической теории электромагнетизма, где он отсутствует, это пожалуй разве только чистая электростатика.
(Здесь формулы приведем в системе единиц СИ, в виде для вакуума[3], где есть варианты для вакуума — для среды; запись в другом виде и подробности — см. по ссылкам).
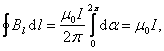