О нормальной системе мнк при полиномиальной аппроксимации.

Возьмем в качестве базисных функций для обобщенного многочлена (3) степенные функции:

В таком случае он превращается в обычный многочлен степени m канонического вида:

Если тоназываетсятригонометрическим полиномом порядка m.

Основная система может состоять также из показательных функцийе^jx и других функций.

Посмотрим, что представляет собой система (4) для вычисления коэффициентов многочлена Q_m(x), если ставится задача аппроксимировать с его помощью некоторую функцию f(x) , заданную в (n+1) узле x₀, x₁, …, x_n.

Будем использовать метод наименьших квадратов.

Согласно этому методу за меру отклонения полинома от данной функцииf(x) на множестве точек x₀, x₁,…, x_n, принимают величину

Очевидно, что F есть функция коэффициентов a₀, a₁,…, a_m, . эти коэффициенты надо подобрать так, чтобы величина F была наименьшей.

Полученный полином Q_m называют аппроксимирующим для данной функции, а процесс построения этого полинома – квадратичной аппроксимацией (аппроксимированием) функции.

Для решения этой задачи воспользуемся общим приемом дифференциального исчисления. Найдем частные производные от , гдеy_i=f(x_i) по всем переменным a₀, a₁,…, a_m .

Приравнивая эти частные производные к нулю, получим систему (m+1) уравнений с (m+1) неизвестными a₀, a₁,…, a_m.

Обозначим

Преобразуя систему (m+1) уравнений и используя эти обозначения, получим:

Систему уравнений относительно a₀, a₁,…, a_m , S₀=n+1.

Можно доказать, что если среди точек x₀, x₁,…, x_n нет совпадающих и m£ n, то определитель системы ¹0 и, следовательно, эта система имеет единственное решение. Полином с такими коэффициентами будет обладать минимальным квадратичным отклонением F.

Если m = n , то Q_m = L_m (x) , причем F=0.

Таким образом, аппроксимирование функций представляет собой более общий процесс, чем интерполирование. Для решения системы уравнений можно применять итерационный процесс, в частности метод Зейделя для нормальных систем, так как матрица из коэффициентов при неизвестных a₀, a₁,…, a_m положительно определенная.

Лекция №13 Сплайн интерполяция

Одним из способов интерполирования на всем отрезке является интерполирование с помощью сплайн функций. Сплайн функцией или сплайном называют кусочно – полиномиальную функцию, определенную на всем отрезке [a,b] и имеющую на этом отрезке некоторое число непрерывных производных.

Рассмотрим частный, но распространенный в вычислительной практике случай, когда сплайн определяется с помощью многочленов третьей степени (кубический сплайн).

Построение кубического сплайна.

Пусть на [a, b] задана непрерывная функция f(x). Введем сетку

и обозначим f_i=f(x_i), i=0,1, ,N.

Сплайном, соответствующим данной функции f(x) и данным узлам , называется функцияS(x), удовлетворяющая следующим условиям:

1. На каждом сегменте [x_i-1, x_i], i=1,2, ,N, функция S(x) является многочленом третьей степени;

2. Функция S(x), а также ее первая и вторая производные непрерывны на [a, b];

3. 

Последнее условие называется условием интерполирования, а сплайн, определяемый условиями 1)-3), называется также интерполяционным кубическим сплайном.

Докажем существование и единственность сплайна, определяемого перечисленными условиями. Приведенное ниже доказательство содержит также способ построения сплайна.

В промежутке между парой соседних узлов интерполяционная функция является многочленом 3-ей степени, который удобно записать в виде:

Коэффициенты многочлена определяют из условий в узлах. Он должен принимать табличные значения:

(1)

Число уравнений в два раза меньше числа неизвестных коэффициентов, поэтому для замыкания нужны дополнительные условия. Найдем первую и вторую производные от кубического многочлена:

(2)

Потребуем непрерывности этих производных (т. е. гладкости гибкой линейки) во всех точках, включая узлы. Приравнивая во внутреннем узле х_i правые и левые пределы производных получаем:

3)

Недостающие два условия обычно получают из естественного предположения о нулевой кривизне графика на концах:

, (4)

что соответствует свободно опущенным концам линейки. Но если есть дополнительные сведения об асимптотике функции, то можно записать другие краевые условия.

Уравнения (1-4) образуют систему линейных уравнений для определения 4N неизвестных коэффициентов. Эту систему можно решить методом исключения Гаусса, но выгоднее привести ее к специальному виду.

Уравнение (1) дает сразу все коэффициенты а_i. Из уравнений (3) и (4)

(5)

Подставим (5) в (1), одновременно исключая а_i=f_i-1, получим:

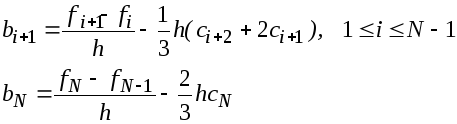(6)

Исключая теперь из (3) b_i и b_i+1 по (6) и d_i по (5), получаем систему уравнений для с_i:

Матрица этой системы 3-х диагональная. Такие системы экономно решаются методом прогонки.

В силу диагонального преобладания система имеет единственное решение.

После нахождения с_i определяются a_i, b_i и d_i и определяется вид кубических многочленов (сплайнов) на каждом отрезке.

Таким образом, доказано, что существует единственный кубический сплайн, определяемый условиями 1)-3) и граничными условиями

Заметим, что можно рассматривать и другие граничные условия.

Можно рассмотреть и более общую задачу интерполяции функции сплайном – многочленом n-ой степени

,

коэффициенты которого кусочно - постоянны, и который в узлах принимает заданные значения и непрерывен вместе со своими (n-1) производными.

На практике наиболее употребительны 2 случая: один при n=3 (кубические многочлены) уже рассмотрен, второй при n-1 (многочлены Ньютона 1-ой степени) соответствует аппроксимации графика ломаной, построенной по узлам; определение коэффициентов при этом очевидно.

ЛЕКЦИЯ №14

ЧИСЛЕННОЕ ИНТЕГРИРОВАНИЕ

ПРОСТЫЕ КВАДРАТУРНЫЕ ФОРМУЛЫ

Общая формула прямоугольников

1. Квадратурная формула левых прямоугольников.

Пусть

2. Формула правых прямоугольников

3. Квадратурная формула средних прямоугольников

Расчет погрешности формул численного интегрирования.

Пусть

Пусть h>0 достаточно мало, x₀=0.

Разложим функцию в ряд Тейлора в окрестности x₀=0.:

Тогда

Локальная погрешность для малого отрезка h -

, то есть

Свойство аддитивности

- погрешность на отрезке [a,b].

Квадратурные формулы Ньютона-Котеса

Если многочленn - степени, то

Это квадратурные формулы интерполяционного типа. Здесь С_к – коэффициенты Котеса

Безразмерные формулы.

Тогда

Итак

Квадратурные формулы интерполяционного типа выглядят следующим образом:

Свойства коэффициентов Котеса

Важные частные случаи n=1, n=2

1. Квадратурная формула трапеций (n=1)

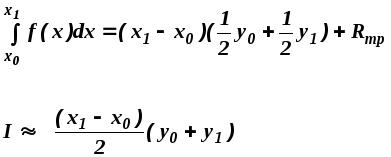
или, используя запись интерполяционного многочлена в форме Ньютона, получим:

Остаточный член для

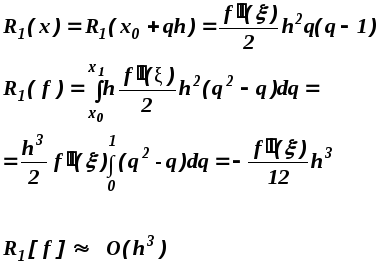
2. Квадратурная формула Симпсона (формула парабол) (n=2)

или, используя запись интерполяционного многочлена в форме Ньютона, получим:

Итак

- формула Симпсона на отрезке

Остаточный член для

3. Частные формулы Ньютона - Котеса, n=k, n=3,4,5…

Общая формула интерполяционного типа имеет вид:

k
1	1/2	1	1
2	1/3	1	4	1
3	3/8	1	3	3	1
4	2/45	7	32	12	32	7

Составные квадратурные формулы.

1. Общая формула трапеций.

2. Составная формула Симпсона
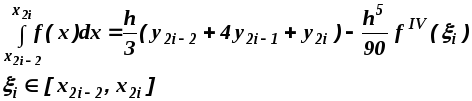