2. Операции над векторами

Над векторами по определённым правилам можно выполнять линейные операции: складывать их, умножать на число, вычитать. Введём линейные операции над векторами.

Произведением вектора

на действительное число  называется вектор

т.е. при умножении вектора на число каждая его координата умножается на это число.

Зная вектор

можно получить противоположный вектор

Суммой векторов

и

называется вектор

,

т.е. при сложении векторов одной и той же размерности их соответствующие координаты почленно складываются.

Если в плане продаж сети торговых предприятий продажи товаров определить как положительные уровни товаров, а затраты на продажи – как отрицательные, то получим вектор затрат-продаж

,

где

-

продажи (затраты) k – м предприятием товара i, а k = 1, 2, 3,…, m .

Суммарный вектор затрат-продаж y определяется суммированием векторов затрат-продаж всех mпредприятий сети:

Сумма противоположных векторов даёт нулевой вектор:

При вычитании двух векторов одной и той же размерности их соответствующие координаты почленно вычитаются:

Линейные операции над векторами удовлетворяют следующим свойствам.

Свойство 1.

Свойство 2.

Свойство 3.

Свойство 4.

Свойство 5.

Свойство 6.

Скалярным произведением двух векторов

и

называется число

равное сумме произведений соответствующих координат векторов.

В экономических задачах можно рассматривать скалярное произведение вектора цен p на вектор объёма проданных товаров x . Скалярное произведение px в этом случае даёт суммарную стоимость проданных товаров x при ценах p . Например, если объём всех товаров, проданных предприятием, выражается вектором x = (400; 750; 200; 300), элементы которого означают соответственно количество товаров различных групп, а цены в одних и тех же денежных единицах заданы в соответствующем порядке вектором p = (3; 2,1; 1,2; 0,5), то скалярное произведение

выражает суммарную стоимость всех товаров x .

Скалярное произведение векторов обладает следующими свойствами:

Свойство 1.

, причём лишь при

Свойство 2.

Свойство 3.

Свойство 4.

Число

равное квадратному корню из суммы квадратов координат вектора, называется модулем (или длиной) вектора

Пример 1. Найти длину вектора x = (3; 0; 4).

Решение. Длина вектора равна

Два вектора называют ортогональными, если их скалярное произведение равно нулю.

Пример 2. Ортогональны ли векторы x = (3; 0; 1; -1) y = (-2; 5; 6; 0)?

Решение. Найдём скалярное произведение

Итак, два данных вектора ортогональны.

Б)  Скалярное произведение

     Скалярное произведение векторов и :

где - угол между векторами и ; если либо , то

     Из определения скалярного произведения следует, что где, например, есть величина проекции вектора на направление вектора .

     Скалярный квадрат вектора:

     Свойства скалярного произведения:

     Скалярное произведение в координатах

     Если то

     Угол между векторами

     

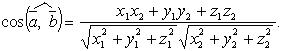
     Векторное произведение

     Векторное произведение векторов и - вектор, обозначаемый или для когорого:

     1) ( - угол между векторами и , );

     2)

     3) тройка , , - правая.

     Свойства векторного произведения: если , то равен площади параллелограмма, построенного на приведенных к общему началу векторах и .

Алгебра (логика) высказываний