26.Непрерывность функции, геометрический смысл , критерий непрерывности.

Ответ:Непрерывная функция — функция без «скачков», то есть такая, у которой малые изменения аргументаприводят к малым изменениям значения функции.

Непрерывная функция, вообще говоря, синоним понятия непрерывное отображение, тем не менее чаще всего этот термин используется в более узком смысле — для отображений между числовыми пространствами, например, навещественной прямой. Эта статья посвящена именно непрерывным функциям, определённым на подмножестве вещественных чисел и принимающим вещественные значения. Свойства[править|править вики-текст]

Локальные[править|править вики-текст]

• Функция, непрерывная в точке a, является ограниченной в некоторой окрестности этой точки.

• Если функция f непрерывна в точке a и f(a)>0 (или f(a)<0), то f(x)>0 (или f(x)<0) для всех x, достаточно близких к a.

• Если функции f и g непрерывны в точке a, то функции f+g и f⋅g тоже непрерывны в точке a.

• Если функции f и g непрерывны в точке a и при этом g(a)≠0, то функция f/g тоже непрерывна в точке a.

• Если функция f непрерывна в точке a и функция g непрерывна в точке b=f(a), то их композицияh=g∘f непрерывна в точке a.

Глобальные[править|править вики-текст]

• Функция, непрерывная на отрезке (или любом другом компактном множестве),равномерно непрерывнана нём.

• Функция, непрерывная на отрезке (или любом другом компактном множестве), ограничена и достигает на нём свои максимальное и минимальное значения.

• Областью значений функции f, непрерывной на отрезке [a,b], является отрезок [minf, maxf], где минимум и максимум берутся по отрезку [a,b].

• Если функция f непрерывна на отрезке [a,b] и f(a)⋅f(b)<0, то существует точка ξ∈(a,b), в которой f(ξ)=0.

• Если функция f непрерывна на отрезке [a,b] и число φ удовлетворяет неравенству f(a)<φ<f(b) или неравенству f(a)>φ>f(b), то существует точка ξ∈(a,b), в которой f(ξ)=φ.

• Непрерывное отображение отрезка в вещественную прямую инъективнов том и только в том случае, когда данная функция на отрезке строгомонотонна.

• Монотонная функцияна отрезке [a,b] непрерывна в том и только в том случае, когда область ее значений является отрезком с концами f(a) и f(b).

• Если функции f и g непрерывны на отрезке [a,b], причем f(a)<g(a) и f(b)>g(b), то существует точка ξ∈(a,b), в которой f(ξ)=g(ξ). Отсюда, в частности, следует, что любое непрерывное отображение отрезка в себя имеет хотя бы одну неподвижную точку.

27.Свойства функций непрерывных в точке. Арифметические свойства непрерывных функций. Ответ: Свойства функций, непрерывных в точке

Поскольку точки непрерывности функциизадаются условием, то часть свойств функций, непрерывных в точке, следует непосредственно из свойств пределов. Сформулируем их в виде следующей теоремы.

        Теорема 3.1   Пусть функции инепрерывны в точке. Тогда функции,,непрерывны в точке. Если, то функциятакже непрерывна в точке.

        Доказательство.     Оно сразу же следует из теорем о пределах 2.8, 2.9, 2.10 и следствия 2.5.      

Как непосредственное следствие этой теоремы получается следующее

        Предложение 3.3   Рассмотрим множество всех функций, определённых в некоторой фиксированной окрестности точкии непрерывных в этой точке. Тогда это множествоявляется линейным пространством, то есть замкнуто относительно сложения и умножения на постоянные:

        Доказательство.     Действительно, постоянные и-- это непpеpывные функции (в любой точке); по пpедыдущей теоpеме тогда непpеpывны в точкепpоизведенияи. Но тогда по этой же теоpеме непpеpывна в точкеи сумма.

        Теорема 3.2   Пусть функции итаковы, что существует композиция,. Пусть функциянепрерывна в точке, а функциянепрерывна в соответствующей точке. Тогда композициянепрерывна в точке.

        Доказательство.     Заметим, что равенство означает, что прибудет. Значит,

(последнее равенство следует из непрерывности функции в точке). Значит,

а это равенство означает, что композиция непрерывна в точке.

Заметим, что, очевидно, в предыдущих двух теоремах можно было бы заменить базу на односторонние базыилии получить аналогичные утверждения для непрерывности слева или справа:

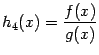        Теорема 3.3   Пусть функции инепрерывны слева (справа) в точке. Тогда функции,,непрерывны слева (соотв. справа) в точке. Если, то функциятакже непрерывна слева (спpава) в точке.

        Теорема 3.4   Пусть функция непрерывна слева (справа) в точке, а функциянепрерывна в точке. Тогда композициянепрерывна слева (соотв. справа) в точке.

28.преход к пределу под знаком непрерывной функции. Непрерывность сложной и обратной функции.. непрерывность элементарных функций.

Ответ: Если lim f(x)=A, а функция g непрерывна в точке А, то lim g(f(x))=g(lim f(x)) . Определение 1. Функция f(x) называется непрерывной в точке x0, если .

Дадим несколько расшифровок этого важнейшего определения.

а) Вспоминая понятие предела,запишем непрерывность f(x) в точке х0 в виде

б) Так как х₀=lim x, то непрерывность в точке х₀ можно записать в виде

Отсюда следует важнейшее свойство непрерывной функции: для непрерывной функции можно переставлять местами знак функции и знак предельного перехода

в) Обозначим x=x-x₀ (приращение аргумента) и f=f(x)-f(x₀) (приращение функции). Тогда непрерывность в точке х₀ означает, что , т.е. бесконечно-малому приращению аргумента соответствует бесконечно-малое приращение функции.

Введем обозначения:

если эти пределы существуют.

Определение 2. Функция f(x) называется непрерывной в точке х₀ слева (справа) если f(x₀)=f(x₀ – 0) (f(x₀)=f(x₀+0)). Очевидно,что непрерывность в точке х₀ означает непрерывность слева и справа одновременно.

Определение 3. Функция f(x) называется непрерывной на некотором множестве Х, если она непрерывна в каждой точке этого множества, т.е. если

Обратите внимание, где стоит квантор, это важно.

Определение. Если функция f(x) не является непрерывной в точке х₀, то говорят, что в точке х₀ функция f(x) имеет разрыв.