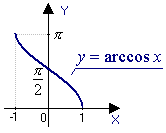11.Отображения ( функция), область определения, образы множеств при отображении , множество значений функции и её график.

Ответ: Отображением множества E в множество F, или функцией, определенной на E со значениями в F, называется правило, или закон f, который каждому элементу ставит в соответствие определенный элемент.

Элемент называютнезависимым элементом, или аргументом функции f, элемент называютзначением функции f, илиобразом; при этом элемент называетсяпрообразом элемента .

Отображение (функцию) обычно обозначают буквой f или символом , указывая тем самым, чтоf отображает множество E в F. Употребляется также обозначение , указывающее, что элементуx соответствует элемент f(x). Иногда функцию удобно задавать посредством равенства, в котором содержится закон соответствия. Например, можно говорить, что "функция f определена равенством ". Если "y" - общее наименование элементов множества F, т. е. F = {y}, то отображение записывают в виде равенстваy = f(x) и говорят, что это отображение задано явно.

2. Образ и прообраз множества при заданном отображении

Пусть задано отображение и множество.

Множество элементов из F, каждый из которых является образом хотя бы одного элемента из D при отображении f, называется образоммножества D и обозначается f(D).

Очевидно, .

Пусть теперь задано множество .

Множество элементов таких, что, называетсяпрообразом множества Y при отображении f и обозначается f ^-1(Y).

Если , то. Если при каждоммножествоf ^-1(y) состоит не более чем из одного элемента , тоf называетсявзаимно однозначным отображением E в F. Впрочем, можно определить взаимно однозначное отображение f множества E на F.

Отображение называется:

- инъективным (или инъекцией, или взаимно однозначным отображением множества E в F), если , или еслиуравнениеf(x) = y имеет не более одного решения;

- сюръективным (или сюръекцией, или отображением множества E на F), если f(E) = F и если уравнениеf(x) = y имеет по крайней мере одно решение;

- биективным (или биекцией, или взаимно однозначным отображением множества E на F), если оно инъективно и сюръективно, или если уравнениеf(x) = y имеет одно и только одно решение.

3. Суперпозиция отображений. Обратное, параметрическое и неявное отображения

1) Пусть и. Поскольку, то отображениеg каждому элементу относит определенный элемент.

Таким образом, каждому посредством правилапоставлен в соответствие элемент

Тем самым определено новое отображение (или новая функция), которое назовем композицией отображений, или суперпозицией отображений, или сложным отображением.

2) Пусть - биективное отображение иF = {y}. В силу биективности f каждому соответствует единичный образx, который обозначим через f ^-1(y), и такой, что f(x) = y. Таким образом, определено отображение , которое называетсяобратным отображению f, или обратной функцией функции f.

Очевидно, отображение f обратно отображению f ^-1. Поэтому отображения f и f ^-1 называют взаимно обратными. Для них справедливы соотношения

3) Пусть

причем хотя бы одно из этих отображений, например , биективно. Тогда существует обратное отображение, а значит,.

Определенное таким образом отображение называется заданным параметрически с помощью отображений ; причем переменная изназываетсяпараметром.

4) Пусть на множестве определено отображение, где множествосодержит нулевой элемент. Предположим, что существуют множестватакие, что при каждом фиксированномуравнениеимеет единственное решение. Тогда на множествеE можно определить отображение , ставящее каждомув соответствие то значение, которое при указанномx является решением уравнения .

Относительно так определенного отображения

говорят, что оно задано неявно посредством уравнения .

5) Отображение называетсяпродолжением отображения , аg - сужением отображения f, если и.

Сужение отображения на множествоиногда обозначают символом.

6) Графиком отображения называется множество

Ясно, что .

12. монотонные функции. Обратная функция, теорема существования. Функции y=arcsinx y=arcos x х свойства и графики.

Ответ: Моното́нная фу́нкция — это функция, приращение которой не меняет знака, то есть либо всегда неотрицательно, либо всегда неположительно. Если в дополнение приращение не равно нулю то функция называется стро́го моното́нной.

.Пусть имеется функция f(x) определенная на отрезке <a,b>, значения которой принадлежат некоторому отрезку <c,d>. Если

 ,

то говорят, что на отрезке <c,d> определена функция, обратная к функции f(x) и обозначают это так:x=f^(-1)(y).

Обратите внимание на отличие этого определения от определения заполненности отрезка <c,d> сплошь. В определении f^(-1)(…) стоит квантор , т.е. значение х, обеспечивающее равенство y=f(x), должно быть единственным, в то время как в определении заполненности отрезка<c,d> сплошь стоит квантор , что говорит о том, что может быть несколько значений х, удовлетворяющих равенству y=f(x).

Обычно, говоря об обратной функции, заменяют х на у а y на x(x «y) и пишут y=f^(-1)(x). Очевидно, что исходная функция f(x) и обратная функция f^(-1)(x) удовлетворяют соотношению

f^(-1)(f(x))=f(f^(-1)(x))=x.

Графики исходной и обратной функции получаются друг из друга зеркальным отображением относительно биссектрисы первого квадранта.

Теорема. Пусть функция f(x) определена, непрерывна и строго монотонно возрастает (убывает) на отрезке [a,b]. Тогда на отрезке [f(a),f(b)] определена обратная функция f^(-1)(x), которая также непрерывна и строго монотонно возрастает (убывает).

Доказательство.

Докажем теорему для случая, когда f(x) строго монотонно возрастает.

1. Существование обратной функции.

Так как по условию теоремы f(x) непрерывна, то, согласно предыдущей теореме, отрезок [f(a),f(b)] заполнен сплошь. Это означает, что .

Докажем, что х единственно. Действительно, если взять х’>x, то будет f(x’)>f(x)=y и поэтому f(x’)>y. Если взять х’’<x, то будет f(x’’)<f(x)=y и поэтому f(x’’)<y. В обоих случаях f(x)¹ y и поэтому x единственно. Следовательно, х=f^(-1)(y) и f^(-1)(…) существует.

2. Монотонность обратной функции.

Сделаем обычную замены x «y и будем писать y= f^(-1)(x). Это значит, что x=f(y).

Пусть x₁>x₂. Тогда:

y₁= f^(-1)(x₁); x₁=f(y₁)

y₂= f^(-1)(x₂); x₂=f(y₂)

Какое же соотношение между y₁ и y₂? Проверим возможные варианты.

а) y₁<y₂? Но тогда f(y₁)<f(y₂) и x₁<x₂, а у нас было x₁>x₂.

б) y₁=y₂? Но тогда f(y₁)=f(y₂) и x₁=x₂, а у нас было x₁>x₂.

в) Остается единственный вариант y₁>y₂, т.е. Но тогда f^(-1)(x₁)>f^(-1)(x₂), а это и означает, что f^(-1)(…) строго монотонно возрастает.

3. Непрерывность обратной функции.

Т.к. значения обратной функции заполняют сплошь отрезок [a,b], то по предыдущей теоремеf^(-1)(…) непрерывна. <

<="" a="" style="color: rgb(255, 68, 0);">

y = arcsin x	y = arccos x
функция обратная функции y = sin x, -/ 2x/ 2	функция обратная функции y = cos x, 0 x

<="" a="" style="color: rgb(0, 0, 0); font-family: Arial; font-size: 11px; font-style: normal; font-variant: normal; font-weight: normal; letter-spacing: normal; line-height: normal; orphans: auto; text-align: start; text-indent: 0px; text-transform: none; white-space: normal; widows: auto; word-spacing: 0px; -webkit-text-stroke-width: 0px; background-color: rgb(0, 171, 160);">

Свойства функций

	y = arcsin x	y = arccos x
ОБЛАСТЬ ОПРЕДЕЛЕНИЯ:	[-1; 1]	[-1; 1]
ОБЛАСТЬ ЗНАЧЕНИЙ:		[0; )
ЧЕТНОСТЬ, НЕЧЕТНОСТЬ:	нечетная	ни четная, ни нечетная
НУЛИ:	y = 0 при x = 0	y = 0 при x = 1
ПРОМЕЖУТКИ ЗНАКОПОСТОЯНСТВА:	y > 0, при x (0;]y < 0, при x [-1; 0)	y = 0 при x = 1  y > 0 при x [-1; 1)
ЭКСТРЕМУМЫ:	нет		нет
ПРОМЕЖУТКИ МОНОТОННОСТИ:	возрастает на всей области определения	убывает на всей области определения

arcsin x + arccos x = /2

<="" a="" style="color: rgb(255, 68, 0); font-family: Arial; font-size: 11px; font-style: normal; font-variant: normal; font-weight: normal; letter-spacing: normal; line-height: normal; orphans: auto; text-align: start; text-indent: 0px; text-transform: none; white-space: normal; widows: auto; word-spacing: 0px; -webkit-text-stroke-width: 0px; background-color: rgb(0, 171, 160);">

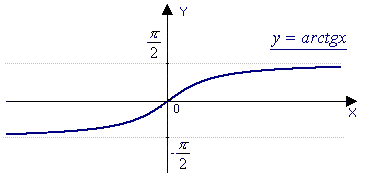
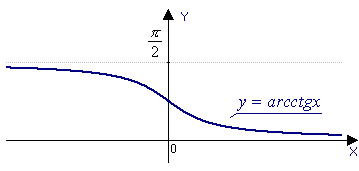
y = arctg x	y = arcctg x
функция обратная функции y = tg x, -/ 2 < x </ 2	функция обратная функции y = ctg x, 0 < x <

13.композиция функций. Элементарные функции. Функции y=arctg x , y = arcctg x, их свойства и графики.

Ответ: В математике компози́ция фу́нкций (суперпози́ция фу́нкций) — это применение одной функции к результату другой.

Композиция функций G и F обычно обозначается G∘F, что обозначает применение функции G к результату функции F.

Пусть F:X→Y и G:F(X)⊂Y→Z две функции. Тогда их композицией называется функция G∘F:X→Z, определённая равенством:

(G∘F)(x)=G(F(x)),x∈X.

Элементарные функции — функции, которые можно получить с помощью конечного числа арифметических действий и композиций из следующих основных элементарных функций^[1]:

• алгебраические:

  • степенная;

  • рациональная.

• трансцендентные:

  • показательная и логарифмическая;

  • тригонометрические и обратные тригонометрические.

Каждую элементарную функцию можно задать формулой, то есть набором конечного числа символов, соответствующих используемым операциям. Все элементарные функции непрерывны на своей области определения.

Иногда к основным элементарным функциям относят также гиперболические и обратные гиперболические функции, хотя они могут быть выражены через перечисленные выше основные элементарные функции.

<="" a="" style="color: rgb(255, 68, 0); font-family: Arial; font-size: 11px; font-style: normal; font-variant: normal; font-weight: normal; letter-spacing: normal; line-height: normal; orphans: auto; text-align: start; text-indent: 0px; text-transform: none; white-space: normal; widows: auto; word-spacing: 0px; -webkit-text-stroke-width: 0px; background-color: rgb(0, 171, 160);">

y = arctg x	y = arcctg x
функция обратная функции y = tg x, -/ 2 < x </ 2	функция обратная функции y = ctg x, 0 < x <

	y = arctg x	y = arcctg x
ОБЛАСТЬ ОПРЕДЕЛЕНИЯ:	R	R
ОБЛАСТЬ ЗНАЧЕНИЙ:		(0; )
ЧЕТНОСТЬ, НЕЧЕТНОСТЬ:	нечетная	ни четная, ни нечетная
НУЛИ:	y = 0 при x = 0	нулей нет
ПРОМЕЖУТКИ  ЗНАКОПОСТОЯНСТВА:	y > 0, при x (0;]y < 0, при x (-; 0)	y > 0 при x R
ЭКСТРЕМУМЫ:	нет	нет
ПРОМЕЖУТКИ  МОНОТОННОСТИ:	возрастает при x R	убывает при x R

arctg x + arcctg x = /2