6. Дискретные сигналы и системы

   1. Преобразование спектра при дискретизации системы.

Рассмотрим равномерную дискретизацию сигнала X(t) выполняемую с помощью импульсного элемента

На выходе импульсного элемента будет определяться по формуле:

X_d(t) = X(t)p(t),

где p(t) –дискредитируемая последовательность импульсов.

p(t) =

Разложить данную функцию в ряд Фурье, по схеме комплексно-экспоненциальной функции получим:

p(t) = ,

где C_K = ;

Тогда в результате дискретизации:

X_D(t)= *x(t)* .

2. Дискретно непрерывное и дискретное преобразование Фурье.

Разложение непрерывного сигнала x(t) в комплексный ряд Фурье может быть распространено и на расположение дискретных сигналов, которые записываются решетчатой функцией вида x[n], которая может быть получена в результате дискретизации x(t).

Значение дискретной последовательности x[n] будет совпадать с отчётами следующего вида:

X(n T₀)=x(t)

t<nT₀

Спектром последовательности x[n] называют комплексную функцию :

X ( ) = = (14)

Выражение (14) эквивалентно разложению спектральной функции X[n] в комплексный ряд Фурье, при этом коэффициенты ряда соответствуют последовательности :

x[n] = X( (15)

(14) и (15) – пара преобразований Фурье (дискретное непрерывное преобразование Фурье (ДНПФ)).

3. Быстрое преобразование Фурье(самостоятельно)

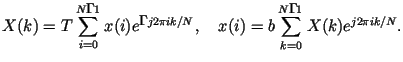(1.50)

Основная идея БПФ состоит в разбиении исходного преобразования (1.50) на несколько частей, каждую из которых можно вычислить отдельно, затем линейно просуммировать с остальными, чтобы получить исходное преобразование. Эти части меньшего размера можно, в свою очередь, разбить на еще меньшие. Пусть длина временного ряда равна .Если использовать деление исходного преобразования (1.50) на каждом шаге на две части, то исходный временной ряд будет состоять из частей так, что , тогда для выполнения вычислений потребуется операций сложения и операций умножения на каждом шаге, что составляет примерно операций. Это значительно меньше тех операций, которые необходимы при вычислениях по формуле (1.50). Эффективность алгоритма БПФ линейно возрастает с ростом длины реализации.

4. Дискретно-косинусное преобразование.

Используем ДПФ перейдем к дискретно-косинусному преобразованию используя в схемах сжатие сигналов, основывающиеся на методе ортогональных преобразований.

Верхний ряд:

1. АЦП

2. Блок буферной памяти

3. Прямое ортогональное преобразование

4. Блок кодирования коэффициентов преобразования

Нижний ряд:

1. Блок буферной памяти

2. Блок декодирования коэффициентов преобразования

3. Обратное ортогональное преобразование

4. ЦАП (цифро-аналоговое преобразование)

Входной аналоговый сигнал с помощью АЦП преобразуется в цифровую последовательность x[n] после чего запоминается в блоке буферной памяти. Накопленная выборка цифровой последовательности длинной n, поступает в блок прямого ортогонального преобразования, где вычисляется x(t). Прямое ортогональное преобразование должно обладать такими свойствами, чтобы последовательность x(l) имело малое значение значимых членов. Кодированию подвергаются члены последовательности x(k), которые переносят существенную информацию и за счет этого достигается сжатие сигнала. После кодирования последовательность поступает в блок декодирования, в котором выполняется обратный процесс.

Прямое и обратное ДКП (дискретно-косинусное преобразование) x[n]:

X (k) = λ(k) (16)

N- длина выборки x[n]

X (k) –коэффициент ДКП

λ(k) – совокупность весовых функций