3.2.3. Пряма лінія на площині. Основні задачі.

Кут між двома прямими і умови паралельності і перпендикулярності двох прямих

Нехай прямі L₁ і L₂ задані рівняннями з кутовими коефіцієнтами і (див. рис. 24).

П отрібно знайти кут, на який треба повернути в позитивному напрямі пряму L1 навколо точки їх перетину до збігу з прямій L2.

○ Маємо (теорема про зовнішній кут трикутника) або . Я

рис. 24.

кщо , то

.

Але , , тому

, (2.12)

звідки легко отримаємо величину шуканого кута.

Якщо потрібно обчислити гострий кут між прямими, не враховуючи, яка пряма є першою, яка — другою, то права частина формули (2.12) береться по модулю, тобто .

Якщо прямі L₁ і L₂ паралельні, то і . З формули (2.12) виходить , тобто . і навпаки, якщо прямі L₁ і L₂ такі, що , то прямі паралельні. Отже, умовою паралельності два прямих є рівність їх кутових коефіцієнтів: .

Якщо прямі L₁ і L₂ перпендикулярні, то . Отже . Звідси, тобто (або ) . Справедливо і зворотне твердження. Таким чином, умовою перпендикулярності прямих є рівність .●

Відстань від точки до прямої

Нехай задана пряма L рівнянням і точка M₀(x₀;y₀) (див. рис. 25). Потрібно знайти відстань від точки М₀ до прямій L.

рис. 25.

Розв’язок: Відстань d, від точки М₀ до прямою L рівно модулю проекції вектора , де M₁(x₁;y₁) - довільна точка прямої L, на напрям нормального вектора . Отже

.

Оскільки точка M₁(x₁;y₁) належить прямою L, то, тобто . Тому

(2.13)

що і потрібно було отримати.

Приклад 2.3. Знайти відстань від точки M₀(2;-1) до прямій .

○ По формулі (2.13) отримуємо .●

Тема 3.3. Лінії другого порядку на площині.

3.3.1. Основні поняття

Розглянемо лінії, визначувані рівняннями другого порядку відносно поточних координат

Ах²+2Вху+Су²+2Dх+2Еу+F=0. (3.1)

Коефіцієнти рівняння — дійсні числа, але принаймні одне з чисел А, В або С відмінне від нуля. Такі лінії називаються лініями (кривими) другого порядку. Нижче буде встановлено, що рівняння (3.1) визначає на площині коло, еліпс, гіперболу або параболу. Перш, ніж переходити до цього твердження, вивчимо властивості перерахованих кривих.

3.3.2. Коло

П ростою кривою другого порядку є коло. Нагадаємо, що колом радіусу R з центром в точці М₀ називається множина всіх точок М площині, які задовольняють умову М₀М=R. Нехай точка М₀ в прямокутній системі координат Оху має координати х₀,у₀, а М(х; у) — довільна точка кола (див. рис. 26).

Тоді з умови М₀М=R отримуємо рівняння

,

рис. 26.

тобто

(x-x₀) ²+(у-y₀)²=R² (3.2)

Рівняння (3.2) задовольняють координати будь-якої точки М(х; у) даного кола і не задовольняють координати ніякої точки, які лежать на колі.

Рівняння (3.2) називається канонічним рівнянням кола.

Зокрема, вважаючи х₀=0 і у₀=0, отримаємо рівняння кола з центром на початку координат x₂ + у₂ = R².

Рівняння кола (3.2) після нескладних перетворень прийме вигляд 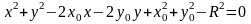. При порівнянні цього рівняння із загальним рівнянням (11.1) кривої другого порядку легко відмітити, що для рівняння кола виконано дві умови:

1) коефіцієнти біля х₂ і у₂ рівні між собою;

2) відсутній член, що містить добуток ху поточних координат.

Розглянемо зворотне завдання. Поклавши в рівнянні (3.1) значення і, отримаємо

. (3.3)

Перетворимо це рівняння:

,

Тобто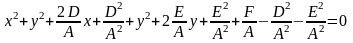

т. е. . (3.4)

Звідси витікає, що рівняння (3.3) визначає коло за умови . Її центр знаходиться в точці , а радіус .

Якщо ж, то рівняння (3.3) має вигляд

.

Йому задовольняють координати єдиної точки . В цьому випадку говорять: «коло виродилося в точку» (має нульовий радіус).

Якщо , то рівняння (3.4), а отже, і рівносильне рівняння (3.3), не визначає ніякої лінії, оскільки права частина рівняння (3.4) негативна, а ліва частина — не негативна (говорять: «коло уявне»).

3.3.3. Еліпс

Канонічне рівняння еліпса

Еліпсом називається множина всіх точок площини, сума відстаней від кожної з яких до двох заданих точок площини, які називаються фокусами, є величина постійна, більша, ніж відстань між фокусами.

П означимо фокуси через F₁ і F₂, відстань між ними через 2с, а суму відстаней від довільної точки еліпса до фокусів — через 2а (див. мал. 49). За визначенням 2a>2с, тобто .

Д

рис. 27.

ля виведення рівняння еліпса виберемо систему координат Оху так, щоб фокуси F₁ і F₂ лежали на осі Ох, а початок координат співпадав з серединою відрізка F₁F₂ . Тоді фокуси матимуть наступні координати:

F₁(-с; 0) і F₂(с; 0).

Нехай М(х;у) — довільна точка еліпса. Тоді, згідно визначенню еліпса,

МF₁ +МF₂=2а, тобто

(3.5)

Це, по суті, і є рівняння еліпса.

Перетворимо рівняння (3.5) до простішого вигляду таким чином:

,

,

,

,

.

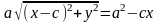Оскільки а > с, то а² - с² > 0. Покладемо

a² – c² = b² (3.6)

Тоді останнє рівняння прийме вид b²х² + а²у² = а²b² або

(3.7)

Можна довести, що рівняння (3.7) рівносильне початковому рівнянню. Воно називається канонічним рівнянням еліпса. Еліпс — крива другого порядку.

Дослідження форми еліпса по його рівнянню

Встановимо форму еліпса, користуючись його канонічним рівнянням.

1. Рівняння (11.7) містить х і у тільки в парних степенях, якщо точка (х;у) належить еліпсу, то йому також належать точки (х;-у), (-х;у), (-х;-у). Звідси витікає, що еліпс симетричний відносно осі Ох і Оу, а також відносно точки O(0; 0), яку називають центром еліпса.

2

рис. 28.

. Знайдемо точки перетину еліпса з осями координат. Поклавши у=0, знаходимо дві точки А₁(а; 0) і A₂(-а; 0), в яких вісь Ох перетинає еліпс (див. рис. 28). Поклавши в рівнянні (3.7) х = 0, знаходимо точки перетину еліпса з віссю Оу: B₁(0;b) і В₂(0;-b). Точки A₁, A₂, B₁, В₂ називаються вершинами еліпса. Відрізки A₁A₂ і B₁В₂, а також їх довжини 2а і 2b називаються великою і малою осями еліпса. Числа а і b називаються відповідно великою і малою пів осями еліпса.

3. З рівняння (3.7) виходить, що кожен доданок в лівій частині не перевершує одиниці, тобто мають місце нерівності і або і . Отже, всі точки еліпса лежать усередині прямокутника, утвореного прямими х = ±a, у = ±b.

4. У рівнянні (3.7) сума невід’ємних доданків і рівна одиниці. Отже, при зростанні одного доданку інше зменшуватиметься, тобто якщо |х| зростає, то |у| зменшується і навпаки.

Додаткові відомості про еліпс

Форма еліпса залежить від відношення . При b = а еліпс перетворюється на коло, рівняння еліпса (3.7) приймає вид х² +у² = а². Як характеристика форми еліпса частіше користуються відношенням .

Відношення половина відстані між фокусами і великої півосі еліпса називається ексцентриситетом еліпса і позначається буквою («эпсилон»):

(3.8)

причому 0<<1, оскільки 0<с<а. З урахуванням рівності (3.6) формулу (3.8) можна переписати у вигляді

,

рис. 29.

тобто

і

Звідси видно, що чим менше ексцентриситет еліпса, тим еліпс буде менш сплюснутим; якщо покласти = 0, то еліпс перетворюється на коло.

Нехай М(х;у) — довільна точка еліпса з фокусами F₁ і F₂ (див. рис. 29).

Довжини відрізків F₁М = r₁, і F₂М = r₂ називаються фокальними радіусами точки М. Очевидно,

r₁ + r₂ =2a .

мають місце формули

і .

Прямі називаються директрисами еліпса. Значення дирек­триси еліпса виявляється наступним твердженням

Теорема 3.1. Якщо r — відстань від довільної точки еліпса до якого-небудь фокуса, d — відстань від цієї ж точки до відповідної цьому фокусу директриси, то відношення є постійною величиною, що дорівнює ексцентриситету еліпса: .

З

рис. 30.

рівності (3.6) випливає, що a > b. Якщо ж a < b, то рівняння (3.7) визначає еліпс, велика вісь якого 2 лежить на осі Оу, а мала вісь 2а — на осі Ох (див. рис. 30). Фокуси такого еліпса знаходяться в точках F₁(0;с) і F₂(0;-с), де .