3.3.5. Парабола

Канонічне рівняння параболи.

Параболою називається множина всіх точок площини, кожна з яких однаково віддалена від даної точки, що називається фокусом, і даної прямої, яка називається директрисою. Відстань від фокуса F до директриси називається параметром параболи і позначається через р (р > 0).

Для виводу рівняння параболи оберемо систему координат Оху так, щоб вісь Ох проходила через фокус F перпендикулярно директрисі в напрямку від директриси до F, а початок координат О розташуємо посередині між фокусом і директрисою (див. рис. 37). В вибраній системі фокус F має координати ( ; 0), а рівняння директриси має вигляд або .

Н

рис. 37.

ехай М(x; у) — довільна точка параболи. З’єднаємо точку М з F. Проведемо відрізок МN пер­пендикулярно директрисі. Згідно означення параболи МF = МN. А з фор­му­лою відстані між двома точками знаходимо:

, а .

Тобто,

.

Піднісши обидві частини рівняння до квадрату, отримаємо

,

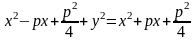тобто

(3.13)

Рівняння (3.13) називається канонічним рівнянням параболи. Пара­бола – лінія другого порядку.

Д ослідження форм параболи за її рівнянням.

1. В рівнянні (3.13) змінна у входить в парному степені, значить, парабола симетрична відносно вісі Ох; вісь Ох є віссю симетрії параболи.

2. Оскільки р > 0, то з (3.13) слідує, що . Тобто , парабола розташована справа від осі Оу.

3. При х = 0 маємо у = 0. Відповідно, парабола проходить через початок координат.

4

рис. 38.

. При необмеженому зростанні х модуль у також необмежено зростає. Парабола у²=2рх має виг­ляд(форму), зображений на рис. 38. Точка О(0;0) називається вершиною параболи, відрізок FМ = r називається фокальним радіусом точки М.

Рівняння у² = -2рх, х² = 2ру, х² = -2ру (р > 0) також визначають параболи. Вони зображені на рис. 39.

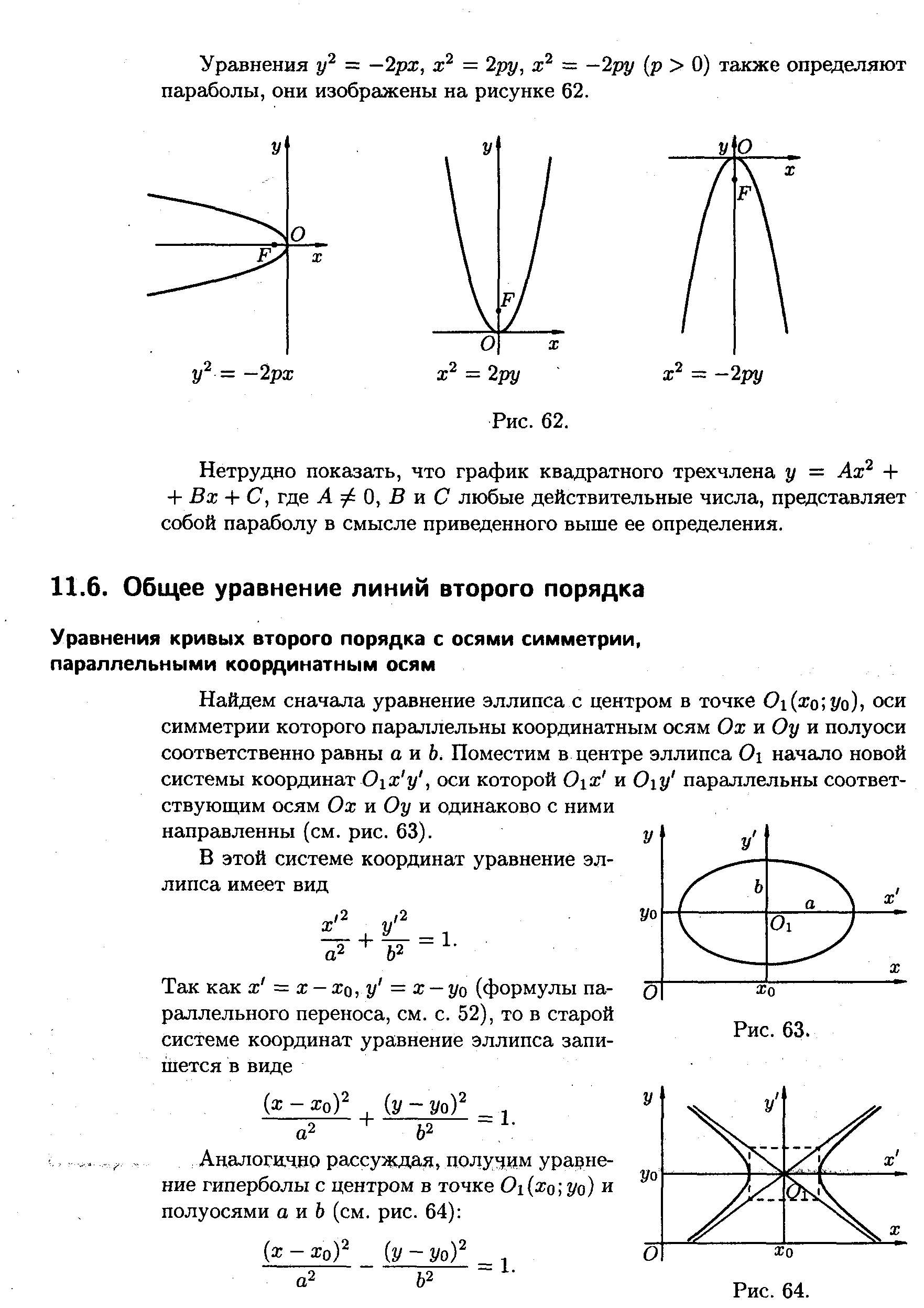
рис. 39.

Неважко показати, що графік квадратного тричлена у = Ах² + Вх + С, где , В і С довільні дійсні числа, представляє собою параболу в сенсі наведеного вище її означення.

3.3.6. Загальне рівняння лінії другого порядку

Рівняння кривих другого порядку з осями симетрії, паралельними координатним осям

З

рис. 40.

найдемо спочатку рівняння еліпса з центром в точці O₁(x₀; y₀), осі симетрії якого паралельна координатним осям Ох і Оу і півосі відповідно рівні a і b. Помістимо в центрі еліпса O₁ початок нової системи координат O₁х'у', вісі якої O₁х' і O₁у' паралельні відповідним осям Ох і Оу і однаково з ними напрямлені (див. рис. 40). В цій системі координат рівняння еліпса має вигляд

.

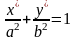Оскільки х' = х – х₀, у' = х - у₀, то в старій системі координат рівняння еліпса запишеться у вигляді

.

Аналогічно міркуючи, отримаємо рівняння гіперболи з центром в точці O₁(х₀;у₀) і півосями а і b (див. рис. 41):

.

рис. 41.

І нарешті параболи, зображені на рис. 42, мають відповідні рівняння.

рис. 42.

Рівняння

Рівняння еліпса, гіперболи, параболи і рівняння кола після перетворень (розкрити дужки, перенести всі члени рівняння в одну сторону, звести подібні доданки, ввести нові позначення для коефіцієнтів) можна записати за допомогою єдиного рівняння виду

, (3.14)

Де коефіцієнти А і С не дорівнюють нулю одночасно.

Виникає питання:чи всяке рівняння виду (3.14) визначає одну з кривих (коло , еліпс, гіперболу, параболу) другого порядку ? Відповідь дає наступна теорема.

Теорема 3.2. Рівняння (3.14) завжди визначає чи коло (при А=С), чи еліпс (при А∙С>0), чи гіперболу (при А∙С<0), чи параболу (при А∙С=0). При цьому можливі випадки виродження: для еліпса (кола) — в точку або уявний еліпс (коло), для гіперболи — в пару прямих, що перетинаються, для параболи — в пару паралельних прямих.

Приклад 3.1. Визначити вид кривої другого порядку, що задана рівнянням

4х² + 5у² + 20х - 30у + 10 = 0.

○ Запропоноване рівняння визначає еліпс (А∙С = 4∙5 > 0). Дійсно, проробимо наступні перетворення:

,

, .

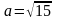Отримаємо канонічне рівняння еліпса з центром в і півосями і .●

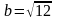Приклад 3.2. Встановити вид кривої другого порядку, що задана рівнянням

х² + 10х - 2у + 11 = 0.

○ Дане рівняння визначає параболу (С = 0). Дійсно,

х² + 10х + 25 - 2у + 11 - 25 = 0,

(х + 5)² = 2у + 14, (х + 5)² = 2(у + 7).

Отрималось канонічне рівняння параболи з вершиною в точці O₁(-5; -7) і p=1.●

Приклад 3.3. Установити вид кривої другого порядку, що задана рівнянням

4x² - у² + 8х - 8у - 12 = 0 (А∙С = - 4 < 0).

○ Перетворимо рівняння:

4(х² + 2х + 1) - (у² + 8у + 16) - 4 + 16 - 12 = 0,

4(х + 1)²-(у + 4)² = 0,

(2(x + 1) + (y + 4))∙(2(x + 1)-(у + 4))=0,

(2x + y + 6)(2х-у-2) = 0.

Це рівняння визначає дві прямі, що перетинаються 2х + у + 6 = 0 і 2х-у-2 = 0.●

Загальне рівняння другого порядку

Розглянемо тепер загальне рівняння другого степеня з двома невідомими:

Ах² + 2Вху + Су² + 2Dх + 2Еу + F = 0. (3.15)

Воно відрізняється від рівняння (3.14) наявністю члена з добутком координат . Можна, шляхом повороту координатних осей на кут а, перетворити це рівняння , щоб позбавитися від члена з добутком координат.

Використовуючи формули повороту осей

, ,

виразимо старі координати через нові:

Виберемо кут а так, щоб коефіцієнт при х'∙у' перетворився на нуль, тобто щоб виконувалась рівність

,

тобто

, (3.16)

тобто

.

Звідси

. (3.17)

Таким чином, при повороті осей на кут а, що задовольняє умову (3.17), рівняння (3.15) зводиться до рівняння (3.14).

Висновок: загальне рівняння другого порядку (3.15) визначає на площині (якщо не рахувати випадків виродження і розпаду) наступні криві: коло, еліпс, гіперболу, параболу.

Зауваження: Якщо А = С, то рівняння (3.17) втрачає сенс. В цьому випадку cos2а=0 (див. (3.16)), тоді 2а = 90°, тобто а = 45°. Так, при А = С систему координат необхідно повернути на 45°.