1. Пусть даны последовательно выполняемые однородные линейные преобразования

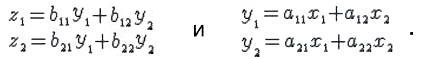
Т.е. в конечном итоге пара     переходит в пару .

Такая операция называется произведением линейных преобразований, а соответствующее преобразование матриц называется произведением матриц.

Непосредственно убеждаемся, что

Соответствующая матрица такова:

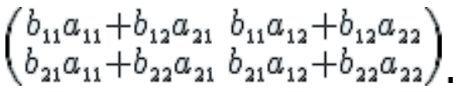
И, окончательно:

Приём умножения матриц:

1. Левую матрицу транспонируем.

2. Тогда искомые матричные элементы получаются как всевозможные взаимные произведения столбцов левой матрицы на столбцы правой матрицы.

3. Место каждого полученного матричного элемента в искомой матрице определяется согласно правилу:

— номер столбца левой матрицы приписывается матричному элементу в качестве номера строки,

— номер столбца правой матрицы приписывается матричному элементу в качестве номера столбца.

Общее правило умножения матриц.

Пусть даны две матрицы А и В с матричными элементами а_ik и b_kj , здесь i, k, j — некоторые натуральные числа, тогда матричные элементы матрицы С =  АВ, вычисляются по формуле:

 

с_ij = а_i1 · b_1 j  + а_i2  · b _2j  + …=

.

 

Здесь знак Σ означает, что выполняется суммирование по всем слагаемым, где индекс k пробегает значения от 1 до n. Но если n =1, то суммирование пропадает, и остаётся только произведение.

Это правило согласуется с вышеприведённым правилом.  

В самом деле,  означает, что строка левой матрицы умножается на столбец правой матрицы. После транспонирования левой матрицы точно такие же результаты будут получаться после умножения столбца одной матрицы на столбец другой. Наконец, от левой матрицы получаем номер строки результата, а от правой — номер столбца. 

Произведение линейных преобразований, т.е. подстановка одного преобразования в другое, возможно, если число функций в первом преобразовании в точности равно числу аргументов во втором преобразовании.

На языке матриц это означает следующее:

Произведение матриц возможно, если число строк в правой матрице равно числу столбцов в левой матрице.

Теперь обратимся к приведённому выше правилу умножения матриц. Понятно, что матрицы можно умножать, если окажется, что у левой (транспонированной) и правой матрицы число строк одинаково.

2. Свойство системы линейных уравнений, содержащей тривиальное уравнение.

Опр. Если в i-том уравнении коэф. При неизв (a11. a12,…) свободные эл-ты равны 0, то любой n-мерный вектор является решением данного уравнения, а само уравнение называется тривиальным

Теорема: СЛУ, содержащая тривиальное уравнение равносильно той же системе без тривиального уравнения.

При решении СЛУ тривиальное уравнение можно не рассматривать

3. Свойство свободных неизвестных в разрешенной системе уравнений.

Определение. Неизвестные называются свободными, для данного набора разрешенных неизвестных СЛУ, если они не вошли в данный набор.

Теорема: Если в разрешенной СЛУ придать значения свободным неизвестным x_r+1,…, x_n произвольное значение k_r+1,…, k_n, т.е. x_r+1=k_r+1, то единственное значение решения в виде n-мерного вектора, у которого значение координат соответствует свободным неизвестным равны соответственно.

Доказательство.

Подставим x_r+1=k_r+1=> x₁=k₁, следовательно k=(k₁,…,k_r,…,k_r+1) является решением по определению.

4. Элементарные преобразования слу.

1) вычеркивание уравнений вида ;

2) перестановка уравнений;

3) умножение любого уравнения на произвольное число, отличное от нуля;

4) сложение обеих частей одного из уравнений системы с соответствующими частями другого уравнения, умноженными на любое число, отличное от нуля.

Теорема. Системы линейных уравнений называются эквивалентными, если множество их решений совпадает, то есть любое решение одной системы одновременно является решением другой, и наоборот.

Систему, эквивалентную данной, можно получить, в частности, заменив одно из уравнений на это уравнение, умноженное на любое отличное от нуля число. Эквивалентную систему можно получить также, заменив одно из уравнений суммой этого уравнения с другим уравнением системы. В общем, замена уравнения системы на линейную комбинацию уравнений даёт систему, эквивалентную исходной.

Система линейных алгебраических уравнений

эквивалентна системе

,

где  — невырожденная матрица.

В частности, если сама матрица  — невырожденная, и для неё существует обратная матрица , то решение системы уравнений можно формально записать в виде

.

8. Определение: Пусть   – произвольный вектор,   – произвольная система векторов. Если выполняется равенство

                    ,                       (1)

то говорят, что вектор   представлен в виде линейной комбинации данной системы векторов. Если данная система векторов   является базисом векторного пространства, то равенство (1) называется разложением вектора   по базису  . Коэффициенты линейной комбинации   называются в этом случае координатами вектора   относительно базиса  .

Теорема. (О разложении вектора по базису.)

Любой вектор векторного пространства можно разложить по его базису и притом единственным способом.

Доказательство.

1) Пусть L произвольная прямая (или ось) и  –базис  . Возьмем произвольный вектор  . Так как оба вектора   и  коллинеарные одной и той же прямой L, то  . Воспользуемся теоремой о коллинеарности двух векторов. Так как  , то найдется (существует) такое число  , что   и тем самым мы получили разложение вектора   по базису   векторного пространства  .

   Теперь докажем единственность такого разложения. Допустим противное. Пусть имеется два разложения вектора   по базису   векторного пространства  :

 и  , где  . Тогда   и используя закон дистрибутивности, получаем:

                       .

Так как  , то из последнего равенства следует, что  , ч.т.д.

2) Пусть теперь Р произвольная плоскость и   – базис  . Пусть   произвольный вектор этой плоскости. Отложим все три вектора от какой-нибудь одной точки этой плоскости. Построим 4 прямых. Проведем прямую  , на которой лежит вектор  , прямую  , на которой лежит вектор  . Через конец вектора   проведем прямую параллельную вектору   и  прямую параллельную вектору  . Эти 4 прямые высекают параллелограмм. См. ниже рис. 3. По правилу параллелограмма  , и  ,  ,   – базис  ,   – базис  .

   Теперь, по уже доказанному в первой части этого доказательства, существуют такие числа  , что

   и  . Отсюда получаем:

 и возможность разложения по базису доказана.

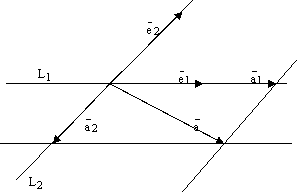
                                         рис.3.

   Теперь докажем единственность разложения по базису. Допустим противное. Пусть имеется два разложения вектора   по базису   векторного пространства  :   и  . Получаем равенство

, откуда следует  . Если  , то  , а т.к.  , то   и коэффициенты разложения равны:  ,  . Пусть теперь  . Тогда  , где  . По теореме о коллинеарности двух векторов отсюда следует, что  . Получили противоречие условию теоремы. Следовательно,   и  , ч.т.д.

3) Пусть  – базис   и пусть   произвольный вектор. Проведем следующие построения.

Отложим все три базисных вектора   и вектор   от одной точки и построим 6 плоскостей: плоскость, в которой лежат базисные векторы  , плоскость   и плоскость  ; далее через конец вектора   проведем три плоскости параллельно только что построенным трем плоскостям. Эти 6 плоскостей высекают параллелепипед:

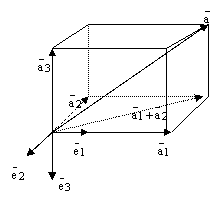
                             рис.4.

По правилу сложения векторов получаем равенство:

                         .                                    (1)

По построению  . Отсюда, по теореме о коллинеарности двух векторов, следует, что существует число  , такое что  . Аналогично,   и  , где  . Теперь, подставляя эти равенства в (1), получаем:

                                              (2)

 и возможность разложения по базису доказана.

   Докажем единственность такого разложения. Допустим противное. Пусть имеется два разложения вектора   по базису  :

 и  . Тогда

        .       (3)

   Заметим, что по условию векторы    некомпланарные, следовательно, они попарно неколлинеарные.

Возможны два случая:   или  .

а) Пусть  , тогда из равенства (3) следует:

            .                        (4)

Из равенства (4) следует, что вектор   раскладывается по базису  , т.е. вектор   лежит в плоскости векторов   и, следовательно, векторы   компланарные, что противоречит условию.

б) Остается случай  , т.е.  .  Тогда из равенства (3) получаем   или

              .                           (5)

Так как  – базис пространства векторов лежащих в плоскости, а мы уже доказали единственность разложения по базису векторов плоскости, то из равенства (5) следует, что   и  , ч.т.д.

9. ЛНЗ часть В1, …, Вm данной системы векторов А1, …, Аn называется максимально линейно незавизимой частью, если после добавления к этой части любого вектора данной системы, не входящего в В1, …, Вm получается ЛЗ часть данной системы векторов.

Если С1, …, Сk не является максимально ЛНЗ частью системы векторов А1, …, Аn, то найдется такой вектор Сk+1 (А1, …, Аn) \ (С1, …, Сk), что система векторов С1, …, Сk, Сk+1 будет ЛНЗ частью системы А1, …, Аn.

Если и система С1, …, Сk, Сk+1 не является максимально ЛНЗ частью системы А1, …, Аn, то найдется такой вектор Сk+2 (А1, …, Аn) \ (С1, …, Сk, Сk+1), что система векторов С1, …, Сk, Сk+1, Сk+2 будет ЛНЗ частью системы А1, …, Аn и т.д.

Через s таких шагов получим максимально ЛНЗ часть С1, …, Сk+s системы векторов А1, …, Аn. Причем полученная система C1, …, Сk+s удовлетворяет условиям определения базиса, т.к. она ЛНЗ. К тому же, если Аj (С1, …, Сk+s), то из определения максимальной линейной независимости следует, что система векторов С1, …, Сk+s, Аj ЛЗ. Тогда по 4-му свойству найдется такой вектор K ≠ θ, что будет выполняться соотношение C1k1 +…+ Ck+sKk+s = Aj, т.е. любой вектор системы А1, …, Аn линейно выражается через вектора С1, …, Сk+s. Следовательно вектора С1, …, Сk+s образуют базис системы А1, …, Аn.

Следствие. Если система векторов содержит хотя бы один ненулевой вектор, то эта система имеет базис.

Пусть А1 ≠ θ, тогда часть данной системы А1, …, Аn, состоящая из одного вектора А1, будет ЛНЗ. По доказанной теореме эту ЛНЗ часть можно дополнить до базиса данной системы.

(стр.28-29)

10. 1º. Оптимальное решение задачи линейного программирования не изменится, если целевую функцию помножить на любое положительное число, либо прибавить к целевой функции любое число.

Доказательство этого утверждения можно провести, используя графический метод решения задачи линейного программирования.

2º. Рассмотрим общую задачу линейного программирования:

1. (max),

2. ≤ bi, i I M={1,2,…,m},

3. = bi, i I \ M={1,2,…,m},

4. Xj ≥ 0, j J N=(1,2,…,n}

Умножив целевую функцию (1) на (-1), рассмотрим новую задачу, а именно,

(1’) f1(X) = = - f(X) (min),

(2’) ≤ bi, i I M={1,2,…,m},

(3’) = bi, i I \ M={1,2,…,m},

(4’) xj ≥ 0, j J N=(1,2,…,n}

Вектор α° является оптимальным решением задачи (1) – (4) на максимум тогда и только тогда, когда α° является оптимальным решением задачи (1’) – (4’) на минимум.

Необходимость. Пусть W есть множество допустимых решений задачи (1) – (4) и задачи (1’) – (4’), а вектор α° является оптимальным решением задачи (1) – (4) на максимум. Тогда, по определению глобального максимума, выполняется неравенство f(α°) ≥ f (α) для любого вектора α W. Умножив последнее неравенство на минус единицу, получим новое неравенство - f(α°) ≤ - f (α) и с учетом обозначения целевой функции задачи (1’) – (4’) имеем f₁(α°) ≤ f₁(α) для любого вектора α W. Откуда, по определению глобального минимума функции f₁(X), вектор α° является оптимальным решением задачи (1’) – (4’) на минимум. Таким образом, необходимость доказана. Для доказательства достаточности следует провести рассуждения в обратной последовательности.

(стр.40-41)

11. 1) задача использования ресурсов;

b – запасы ресурсов, aij – расход каждого i-ого вида ресурса на изготовление единицы j-ой продукции, сj – прибыль

Z(x)=c₁x₁+c₂x₂+…+c_nx_n → max

a₁₁x₁+a₁₂x₂+…+a_1nx_n≤b₁

a₂₁x₁+a₂₂x₂+…+a_2nx_n≤b₂

………………………………

a_m1x₁+a_m2x₂+…+a_mnx_n≤b_m

x_i ≥ 0

2) задача о составлении рациона питания;

b- животные должны получать ежедневно не менее b, aij – содержание iого пит вещества в единице jого вида корма, cj – стоимость единицы jого вида корма.

Z(x)=c₁x₁+c₂x₂+…+c_nx_n → min

a₁₁x₁+a₁₂x₂+…+a_1nx_n≥b₁

a₂₁x₁+a₂₂x₂+…+a_2nx_n≥b₂

………………………………

a_m1x₁+a_m2x₂+…+a_mnx_n≥b_m

x_i ≥ 0

3) Задача транспортных перевозок. В m пунктах производится однородный продукт в количествах a1,a2,…,am единиц, который необходимо в другие n пунктов, в которых этот продукт потребляется в количествах b1,b2,…,bn единиц. Стоимость перевозки одной единицы продукта из (i=1,2,…,m) пункта производства в (j=1,2,…n) пункт потребления равна c_ij денежных единиц, а производится продукта больше, чем потребляется, т.е.

Требуется сформировать план перевозок продукта, при котором все потребности в продукте будут удовлетворены с наименьшими затратами на перевозку.

Определим вектор X = (x₁₁,...,x_ij…, x_mn) как план перевозок между поставщиками и потребителями, где x_ij – количество единиц продукта, которое перевозится из пункта производства i в пункт потребления j, и при чем либо перевозка имеется, либо она отсутствует, т.е. x_ij ≥0, i=1,2,…m; j=1,2,…n, тогда:

- суммарная стоимость всех перевозок;

Из i пункта производства вывозиться единиц продукта не более, чем производится, т.е. x_i1+…+x_ij+…x_in≤a_i , i=1,2,…m;

В j пункт потребления завозится единиц продукта не менее, чем потребляется, т.е. x_1j+…x_ij+…x_mj≥b_j , j=1,2,…n

Таким образом, приходим к математической постановке задачи планирования транспортных перевозок в виде задаче линейного программирования на минимум

Замечание. При математической постановке экономической задачи необходимо:

1. Ввести переменные величины, каждая из которых определяет некоторый управляемый экономический параметр.

2. Сформировать систему ограничений, связывающие введенные переменные, используя условия задачи.

3. Построить функцию цели (качества) выбора значений переменных.

12. Теорема (о существовании опорного решения). Если КЗЛП имеет хотя бы одно допустимое решение, то эта задача имеет и опорное решение.

Рассмотрим КЗЛП

2. =B

Которая имеет хотя бы одно допустимое решение. Из всех допустимых решений данной задачи выберем допустимое решение с наименьшим числом ненулевых координат. Пусть таким решением будет вектор а = (а1,…,a_l,0,…,0), где координаты а_l>0,…, а_l>0 (координаты всегда можно перенумеровать так, что первыми из них станут ненулевые) и докажем, что выбранный вектор является опорным решением задачи (1)-(3).

Предположим противное, а именно, что вектор а не является опорным решением. Тогда по определению опорного решения, векторы А1, А2, …, А_l, соответствующие ненулевым координатам выбранного вектора а, образуют линейно зависимую систему. Из определения линейно – зависимой системы векторов следует, что найдется ненулевой набор чисел k1,k2,…k_l такой, что будет выполняться соотношение

4. А₁k₁+A₂k₂+…+A_lk_l = θ

Так как вектор а является допустимым решением рассматриваемой задачи, то по определению, этот вектор является решением системы линейных уравнений (2). Тогда по определению решения системы уравнений должно выполняться соотношение

5. А₁k₁+A₂k₂+…+A_lk_l = В

Прибавив к соотношению (5) соотношение (4), умноженное ±δ, получим

A₁(a₁±δk₁)+A₂(a₂±δk₂)+…+A_l(a_l±δk_l) = B

Из последнего соотношения по определению решения системы уравнений следует, что векторы a’ = (a₁+δk₁, a₂+δk₂,…,a_l+δk_l,0,…,0) и a” = (a₁-δk₁, a₂-δk₂,…,a_l-δk_l,0,…,0) являются решением СЛУ (2). Если же число δ выбрать так, что оно удовлетворяет арифметической лемме, то координаты векторов a’и a” будут удовлетворять условию (3), а сами векторы будут являться допустимыми решениями задачи (1)-(3) и при этом, хотя бы у одного из этих векторов число ненулевых координат будет меньше, чем l. Это противоречит выбору допустимого вектора а. Следовательно, вектор а является опорным решением задачи (1)-(3).

13. и 14. Свойство. Любому опорному решению КЗЛП соответствует, по крайней мере, один базис системы векторов условий этой задачи.

Пусть вектор а = (0,…,0. a_i1, 0, …, 0, a_i2, 0, …, 0, a_il, 0, … 0) является опорным решением КЗЛП

6. =B

Где a_i1>0, a_i2,>0, …, a_il>0. Тогда по определению в системе векторов условий задачи (1)-(3) векторы A_i1,A_i2,…, A_il, соответствующие ненулевым координатам данного опорного решения, образуют линейно независимую систему векторов, которую можно дополнить до базиса всей системы векторов условий данной задачи. Пусть этим базисом будет система из векторов A_i1,A_i2,…, A_il A_il+1,…, A_ir. Тогда небазисным векторам из системы векторов условий задачи (1)-(3) соответствуют ненулевые координаты опорного решения и по определению векторы A_i1,A_i2,…, A_ir образуют базис опорного решения а.

Следствие (обязательно для 14ого билета). Число ненулевых координат у любого опорного решения а КЗЛП не превышает r = rang { A₁,…, A_n} – ранга системы векторов условий этой задачи.

15. 15. (стр. 52) Свойства базисов опорного решения:

Определение: Опорное решение КЗЛП называется невырожденным, если число его ненулевых координат равно рангу системы векторов условий рассматриваемой задачи.

1. F(X) = ∑ⁿ_i=1 γ_j x_j + γ₀,

2. ∑ⁿ_i=1 A_j x_j = B,

3. x_j≥0, j=1, 2, … , n.

Свойство 2. Невырожденному опорному решению КЗЛП (1)-(3) может соответствовать только один базис системы векторов условий данной задачи.