Доказательство.
Рассмотрим пару симметричных двойственных задач
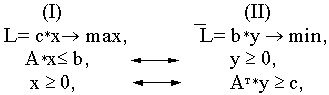
Если одна из пары двойственных задач (I) и (II разрешима, то разрешима и другая задача, причем оптимальные значения целевых функций прямой и двойственной задач совпадают
оптимальные планы задач (I) и (II) соответственно.
Доказательство.
1. Пусть задача (I) разрешима, и пусть
т.е. х* - оптимальное решение. Обозначим M= L(х*).
Тогда по основной лемме существует
для
которого 
Но по основному неравенству двойственности имеем :
Объединяя
последние два соотношения, имеем 
откуда следует, что у* - оптимальное решение задачи (II) и
2. Пусть теперь задача (II) -разрешима. Построим эквивалентную (II) задачу
Задача (II') разрешима, так как задача (II) разрешима. Тогда по пункту 1 двойственная к (II') задача :
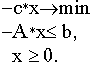
Но эта задача эквивалентна задаче (I). Следовательно, задача (I) разрешима. Ч.т.д.
Вторая теорема двойственности:
Доказательство.
Рассмотрим пару симметрических двойственных задач ЛП
Чтобы допустимые решения х, у пары двойственных задач (I) и (II) были оптимальными необходимо и достаточно, чтобы выполнялись условия :
Необходимость. По условию допустимые решения х, у - оптимальны.
то
из оптимальности решений х, у по первой
теореме двойственности 
В
результате имеем 
Необходимость доказана.
Достаточность. По условию
По первой теореме двойственности получаем, что х, у - оптимальные решения задач (I) и (II).
Достаточность доказана. Ч. Т. Д.
31. Взаимно двойственными задачами линейного программирования называется пара задач вида:
(max),
≤ bi, i I M={1,2,…,m},
= bi, i I \ M={1,2,…,m},
(4) Xj ≥ 0, j J N=(1,2,…,n} и
(1’)
φ(Y)
=
(min),
(2’)
≥ yj, j
J
N={1,2,…,m},
(3’) = yj, j J \ N={1,2,…,m},
(4’) yi ≥ 0, i I M=(1,2,…,m},
Если дана задача ЛП, то для нее всегда можно построить взаимно двойственную задачу ЛП, используя следующие правила.
1º. Одна из пары взаимно двойственных задач ЛП должна быть задачей на максимум и левая часть ее системы условий не больше правой, то есть между левой и правой частями системы условий неравенство вида: ≤. Тогда другая из пары взаимно двойственных задач ЛП должна быть задачей на минимум и левая часть ее системы условий не меньше правой, то есть между левой и правой частями системы условий неравенство вида: ≥.
2º. Для каждой из пары взаимно двойственных задач ЛП можно выписать таблицу, в которой координаты вектора ограничений, входящие в неравенства системы условий, и коэффициенты целевой функции при неотрицательных переменных отмечаются звездочкой. При этом таблица для одной из взаимно двойственных задач ЛП после транспонирования становится таблицей для другой из взаимно двойственных задач ЛП.
(стр.83)
32. Достаточное условие оптимальности опорного решения.
Пусть Ui (i=1,2, …, m), Vj (j=1,2, …, n) потенциалы опорного решения α° = (X11°, …, Xmn°) транспортной задачи линейного программирования. Если для всех не занятых клеток, т.е. Xij° = 0, i=1,2, …, m; j=1,2, …, n выполняется неравенство Ui + Vj ≤ Cij , то опорное решение является оптимальным решением данной задачи.
Метод потенциалов
Пуст вектор α1 = (X11¹, …, Xmn¹) является опорным решением транспортной задачи линейного программирования. Ненулевые координаты этого вектора, т.е. Xij¹ ≠ 0, запишем в соответствующие клетки транспортной таблицы. Если окажется, что заполненных клеток меньше, чем m + n – 1, то в некоторые из оставшихся пустыми клеток транспортной таблицы допишем «жирным» шрифтом нули так, чтобы образовать ацикличный набор из m + n – 1 заполненных клеток.
Шаг 1. Найдем потенциалы опорного решения α1 = (X11¹, …, Xmn¹)
Если для любой из незаполненных клеток, т.е. Xij¹ = 0, i=1,2,…, m; j=1,2,…, n, окажется, что Ui + Vj ≤ Cij, то α1 = (X11¹, …, Xmn¹) является оптимальным решением данной задачи.
Если же найдется клетка (r,s), для которой выполняется неравенство Ur + Vs > Сrs, то строим цикл, одна из вершин которого находится в клетке (r,s), а все остальные вершины находятся в ранее заполненных клетках. Такой цикл сушествует и притом только один. Назовем его циклом пересчета. Каждой вершине цикла пересчета, начиная с вершины (r,s), присвоим поочередно положительные и отрицательные знаки, т.е. знаки + и -.
Среди клеток со знаком минус выберем клетку (k,l) с наименьшей величиной перевозки, т.е. Xkl = min{Xij}. Пусть Xkl = p. Тогда транспортную таблицу заполним следующим образом:
Xij˝ = Xij’, если клетка (i,j) не является вершиной цикла пересчета;
Xij˝ = Xij’ + p, если клетке (i,j) был присвоен знак плюс;
Xij˝ = Xij’ – p, если клетке (i,j) был присвоен знак минус;
клетка (k,l) не заполняется.
Можно доказать, что в результате будет получено новое опорное решение α2 = (X11˝,…Xmn˝), на котором значение целевой функции будет не меньше, чем на первоначальном опорном решении, т.е. f(α2) ≤ f(α1).
Шаг 2. Выполняем шаг 1 для опорного решения α2 = (X11˝,…Xmn˝), и т.д.
Через конечное число шагов будет найдено оптимальное решение.
Стр.100