
- •2. Свойство системы линейных уравнений, содержащей тривиальное уравнение.
- •3. Свойство свободных неизвестных в разрешенной системе уравнений.
- •Доказательство.
- •4. Элементарные преобразования слу.
- •Доказательство.
- •Доказательство.
- •Доказательство.
- •17. Число опорных решений канонической задачи линейного программирования.
- •18. Связь базиса системы векторов условий канонической задачи линейного программирования с базисом некоторого опорного решения этой задачи.
- •19. Теорема об оптимальном решении канонической задачи линейного программирования.
- •Доказательство.
- •Доказательство.
- •26. Теорема о разрешимости кзлп.
- •Доказательство.
- •Доказательство.
- •Доказательство.
- •Доказательство.
- •31. Взаимно двойственными задачами линейного программирования называется пара задач вида:
- •32. Достаточное условие оптимальности опорного решения.
Доказательство.
По условию вектор β=(а1, а2, … , аn, an+1, an+2, … , an+m) является оптимальным решением искусственной задачи. Тогда вектор β является опорным решением этой задачи, а, следовательно, и допустимым решением и, по определению, является решением системы линейных уравнений, то есть выполняется соотношение:
А1а1 + А2а2 + … + Аnan + E1an+1 + E2an+2 + … + Eman+m = B,
Так как an+1= an+2 = … = an+m=0, то последнее равенство можно записать в виде: А1а1 + А2а2 + … + Аnan = B. Откуда, по определению, следует, что вектор а=(а1, а2, … , аn) является допустимым решением исходной задачи (1) – (3).
Так как вектор β=(а1, а2, … , аn, 0, 0, … , 0) является опорным решением искусственной задачи, то ненулевым координатам этого вектора соответствуют линейно независимые векторы условий этой задачи. Тогда некоторые из указанных линейно независимых векторов соответствуют ненулевым координатам вектора а=(а1, а2, … , аn). Следовательно, вектор а является опорным решением исходной задачи (1) – (3).
От противного. Предположим, что существует число an+i>0, i=1, 2, … , m, но при этом исходная задача (1) – (3) имеет допустимое решение а=(k1, k2, … , kn), которое удовлетворяет системе (2) и kj≥0, j=1, 2, … , n. Тогда по определению допустимого решения выполняется соотношение: А1 k1 + А2 k2 + … + Аn kn = B, которое можно переписать в виде:
А1 k1 + А2 k2 + … + Аn kn + An+1 0 + An+2 0 + … + An+m 0 = B.
Откуда следует, что вектор β’=(k1, k2, … , kn, 0, 0, … , 0) является допустимым решением искусственной задачи (4) – (6).
Так как по условию вектор β=(а1, а2, … , аn, an+1, an+2, … , an+m) является оптимальным решением искусственной задачи, то φ(β)≤ φ(β’), что равносильно неравенству: an+1, an+2, … , an+m ≤0 + 0 + … + 0. Однако, по предположению, существует an+i>0, i=1, 2, … , m, следовательно, an+1, an+2, … , an+m >0. Получено противоречие. Таким образом, предположение о существовании допустимого решения исходной задачи является верным. Следовательно, система ограничений исходной задачи является несовместной.
29. 1. Целевая функция исходной задачи (32) – (34) задается на максимум, а целевая функция двойственной (35) – (37) – на минимум. 2. Матрица, составленная из коэффициентов при неизвестных в системе ограничений (33) исходной задачи (32) – (34), и аналогичная матрица в двойственной задаче (35) – (37) получаются друг из друга транспонированием (т. е. заменой строк столбцами, а столбцов – строками). 3. Число переменных в двойственной задаче (35) – (37) равно числу ограничений в системе (33) исходной задачи (32) – (34), а число ограничений в системе (36) двойственной задачи – числу переменных в исходной задаче. 4. Коэффициентами при неизвестных в целевой функции (35) двойственной задачи (35) – (37) являются свободные члены в системе (33) исходной задачи (32) – (34), а правыми частями в соотношениях системы (36) двойственной задачи – коэффициенты при неизвестных в целевой функции (32) исходной задачи. 5. Если переменная xj исходной задачи (32) – (34) может принимать только лишь положительные значения, то j–е условие в системе (36) двойственной задачи (35) – (37) является неравенством вида. Если же переменная xj может принимать как положительные, так и отрицательные значения, то 1 – соотношение в системе (54) представляет собой уравнение. Аналогичные связи имеют место между ограничениями (33) исходной задачи (32) – (34) и переменными двойственной задачи (35) – (37). Если i – соотношение в системе (33) исходной задачи является неравенством, то i–я переменная двойственной задачи . В противном случае переменная уj может принимать как положительные, так и отрицательные значения.
(32):
![]()
при условиях
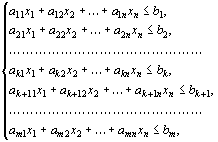 (33)
(33)
![]() (34)
(34)
(35):
![]()
при условиях
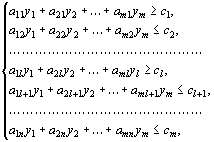 (36)
(36)
![]() (37)
(37)
30. http://www.compmodel.ru/102/217/index.1.html
http://www.compmodel.ru/102/218/index.1.html
Первая теорема двойственности:
