лекции, учебные пособия / конспект лекций / Lekcii / Лекция 2 (Пустовой Д

Показатели эффективности. Функциональные полезности.

Шкалы:

1. номинальные – используются при классификации (различные классификаторы)

2. порядка – позволяют сопоставить объекты по определённым характеристикам (таблицы, шкалы твёрдости)

3. интервалов –

Пример: календари, разница в которых – постоянная величина.

4. отношений –

5. абсолютные – в качестве единиц измерения используются некоторые числа, самые совершенные

6. нечёткие – используются функции принадлежащие нечётким множествам (возраст людей: молодые, старые)

0<М<1

Шкала возраста:

Субъективная вероятность определяется мнением экспертов.

10 20 30 40 50 60 70

7. желательности – обычно задаются в виде:

По ГОСТу:

Очень хорошо	Хорошо	Удовлетворительно	Плохо	Очень плохо
0,8÷1	0,63÷0,8	0,37÷0,63	0,2÷0,37	0÷0,2

Показатели и критерии эффективности (ПЭ)

ПЭ – мера соответствия реального результата операции требуемому.

ПЭ задается функцией w(y)

y(u) – полученный результат

y_тр – требуемый результат

Тогда имеем:

ρ = ρ (y(u), y_тр) и W(u) = M(ρ(y(u), y_тр)), если величины y(u), y_тр случайные.

Здесь М – математическое ожидание

ПЭ может быть скалярным и векторным.

Формы показателей эффективности

1. Функция ρ имеет вид

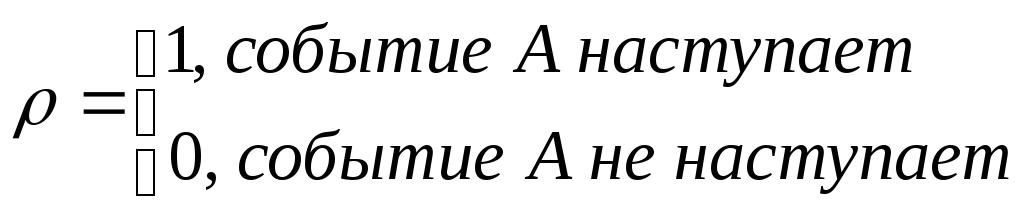
тогда W(U) = P(A) – вероятность наступления события А

2. Функция ρ имеет вид

Виды ПЭ

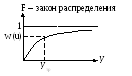1. Вероятностная гарантия – вероятность того, что достигнутая величина больше или меньше некоторой требуемой величины: W(u) = P( y(u)≥y_тр )

Зная y_тр, находим w(u)

2. Вероятностно-гарантированный результат – минимальный результат y_α, получаемый с заданной вероятностной гарантией α.

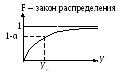
Зная, что α = P(y(u)≥y_α), находим y_α

3. Математическое ожидание – это простой, но малоинформативный показатель, показатель среднего результата.

Критерий эффективности (КЭ)

КЭ – правило, позволяющее сопоставить стратегии, характеризующиеся разной степенью достижения цели, и осуществить направленный выбор стратегии из множества допустимых.

Типы КЭ

1. Критерий пригодности. W(u) ≥ W_тр

2. Критерий оптимальности. W(u^*) = max (W), где u^* Є U, U – множество альтернатив

3. Критерий адаптивности.

Виды критериев пригодности

1. Критерий приемлемого результата

y(u^*) ≥ y_тр, u^* Є U

2. Критерий допустимой гарантии

P(y(u^*)≥y _тр) ≥ P_тр, u^* Є U

3. Критерий допустимого гарантированного результата

y_α(u^*) ≥ y_тр, u^* Є U

4. Критерий наибольшего результата

max ( y(u^*) ), u^* Є U

5. Критерий наибольшего среднего результата

max ( M (y(u^*) ), u^* Є U

6. Критерий наибольшей вероятностной гарантии

max ( P( y(u^*) y_тр ) ) , u^* Є U

Пример: пусть у данных стратегий одинаковое математическое ожидание некоторого показателя эффективности. Дано графическое представление ПЭ. Пусть сплошная линия - первая стратегия, а пунктир – вторая.

Очевидно, что при y_тр<y^* получаем P₂^гар лучше, чем Р₁^гар

А при y_тр>y* получаем P₁^гар лучше, чем Р₂^гар

Вывод: одного математического ожидания недостаточно, чтобы правильно обосновать выбор той или иной стратегии.

Способы выражения предпочтений

1. Сортировка. Множество альтернатив делится на классы и определяется принадлежность каждой из альтернатив введенным классам.

Типы целей: желательные, обязательные, возможные

2. Ранжирование. Расстановка приоритетов целей.

3. Попарное сравнение. Составление квадратной матрицы с количеством строк, равным числу параметров сравнения. На пересечении i-ой строки и j-го столбца ставим 1, если параметр i приоритетнее параметра j.

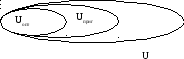
4. Отношения. Бинарные отношения – отношения R в выражении типа d₁ R d₂.

Здесь на месте R может стоять одно из слов: лучше, старше, богаче, сильнее и т.д.

Способы задания бинарных отношений

Пусть дан набор критериев W = {W1, W2,W3}

1. Перечисление элементов множества.

W1W1, W1W2, W1W3, W2W2, W3W2, W3W3 – перечисление пар элементов, в каждой из которых элементы связанны соотношением «не менее предпочтителен»

2. Указание общих свойств.

3. Граф.

Пусть запись W1  W2 значит, что W1 предпочтительнее W2, тогда граф такой:

4. Матрица смежности

	W1	W2	W3
W1	1	1	1
W2	0	1	0
W3	0	1	1

5. Подмножество точек на системе декартовых координат

W1

W2

W3

W1 W2 W3