Все лекции по аналитический геометрии

& :

" 3 - ) !,

. * ! 3 , :

1)3(a + b ) = 3(a ) +3(b ).

2)3(α a ) = α 3(a ) , α R.

/ 1) 2) ,

) 3(α a + β b ) = α 3(a ) + β 3(b ), α , β R.

) 3(α1 f1 + α2 f2 + + αn fn ) = α1 3( f1 ) +α2 3( f2 ) + + αn 3( fn ), α1 ,α2 , ,αn R.

+ III. .

" ( ),

x, y, z . . (

).

( ).

§9.

n

M

πM0

n = ( A, B, C) .

: " π - ,

n - π , n ≠ 0 n π . ' ,

.

. % ) , . . M 0 (x0 , y0 , z0 ) , M 0 π .

" M (x, y, z) - « » , π ,

M (x, y, z) π n M		M = (x − x , y − y		, z − z		) (n, M	M ) = 0
0		0	0	0		0
	A(x − x0 ) + B( y − y0 ) + C(z − z0 ) = 0				.	(9.1)

" , M 0 (x0 , y0 , z0 )

n = ( A, B, C) .

' D = − Ax0 − By0 − Cz0 , & :

Ax + By + Cz + D = 0	(9.2)

" . & ( (9.2) A2 + B2 + C 2 > 0 ( . .

)) ! A, B C ) ): $ (9.2): A1 x + B1 y + C1 z + D1 = 0

D

" C1 ≠ 0 . $ M1 (0, 0, − 1 )

C1

, M1 n1 = ( A1 , B1 , C1 ) .

21

A1 (x − 0) + B1 ( y − 0) + C1 (z + D1 ) = 0

C1

A1 x + B1 y + C1 z + D1 = 0 - , .

: (9.2) :

(9.2) , , A2 + B2 + C 2 > 0 .

!

" .

' :	M	n

π+ ( ).

π− ( ).

	: Ax + By + Cz + D = 0 ,	π	M0
	n = ( A, B, C) - :

* M 0 (x0 , y0 , z0 ) π . M (x, y, z) π + n M 0 M >0

A(x − x0 ) + B( y − y0 ) + C(z − z0 ) > 0

Ax + By + Cz − Ax0 − By0 − Cz0 > 0 M 0 (x0 , y0 , z0 ) π Ax0 + By0 + Cz0 + D = 0 − Ax0 − By0 − Cz0 = D

"

π+ = {(x, y, z) : Ax + By + Cz + D > 0}

π− = {(x, y, z) : Ax + By + Cz + D < 0}

π= {(x, y, z) : Ax + By + Cz + D = 0}

%. ' (9.2),

.

" :

.

% z

( )

: Oxyz - &" 4, n = (n1 , n2 , n3 ) − ,

n = n12 + n22 + n32 = 1,

α , β , γ − .

,

n1 = n cosα = cosα ,

n2 = cos β , n3 = cos γ .

y

n = (cosα , cos β , cos γ ) - .

				:
						cos2 α + cos2 β + cos2 γ = 1 .
x
				" π - ) ,
				OM	0	π , M	0	(x , y , z			) π , n ↑↑ OM	0	,
								0	0	0

n = (cosα , cos β , cos γ ) -

.

M 0 (x0 , y0 , z0 )

nP

22

0 (0,0,0)

π

r = OM 0 = dist(0,π ) .

' , OM 0 = rn = (r cosα , r cos β , cos γ ) , . . M 0 (r cosα , r cos β , cos γ ) .

π , M 0 n : cosα (x − r cosα ) + cos β ( y − r cos β ) + cos γ (z − r cos γ ) =

=x cosα + y cos β + z cos γ − r(cos2 α + cos2 β + cos2 γ ) =

=x cosα + y cos β + z cos γ − r = 0

" :

x cosα + y cos β + z cos γ − r = 0 ,

(cosα , cos β , cos γ ) - π , r -

O( ) π .

: (

). 2 , r = 0 . 5

, ,

(±) .

4 ?

":									x + 2 y + 3z = 0																					~									, 12 +22 +32 = 14
1						x +				2					y +						3							+		4							= 0 ~
~																											z
14										14											14									14
~ −				1				x −		2								y −			3							z −						4					= 0 - .
14										14											14													14
% n = −										1							; −				2						; −			3									− ,
										14											14									14									O .

' : , Ax + By + Cz + D = 0 ,

A2 + B2 + C 2 (±1) , )) !

!.

#

M1 (x1 , y1 , z1 )

	r	M	0 (x0 , y0 , z0 )
			π
0 n		δ = (n, M 0 M1 )

M1 (x1 , y1 , z1 ) .

' δ ≡ prn M 0 M1 :

δ = cosα (x1 − x0 ) + cos β ( y1 − y0 ) + cos γ (z1 − z0 ) = = {x0 cosα + y0 cos β + z0 cos γ = p, . M0 π } = = x1 cosα + y1 cos β + z1 cos γ − r.

" , . * :

δ (M	,π ) ≡ pr					= x cosα + x cos β + x cos γ − r			.
		M	0	M	1
1	n					1	2	3

& ,

.

23

1.δ = dist(M1 ,π ) .

2.δ > 0 M1 0 π ;

δ< 0 M1 0 π .

. * M1 (x1 , y1 , z1 ) π :

d =		Ax1	+ By1 + Cz1	+ D			= dist(M1	,π )	,
			A2 + B2 + C 2

Ax1 + By1 + Cz1 + D = 0 - , x1 , y1 z1 - M1

§10.

:

M (x, y, z) " l - . a -

& l , a ≠ 0 a l .

a* M 0 (x0 , y0 , z0 ) l .

			M (x, y, z) l M			M a	M	M = ta, t R x − x	= ta ,
l M 0	(x0 , y0 , z0 )			0			0	0	1
				− y0 = ta2 , z − z0 = ta3 , t R
			y
	x = x0 + a1t
	y = y	0	+ a t ,	t R	.
			2
	z = z0 + a3t.

" , M 0 (x0 , y0 , z0 )

a = (a1 , a2 , a3 ) .

/ t : t =

x − x0

=

y − y0

=

z − z0

.

a1

a2

a3

3 t a = (a , a , a ) = (l, m, n) :

x − x0

=

y − y0

=

z − z0

1

2

3

l

m

n

" l , M 0 (x0 , y0 , z0 )

a = (l, m, n) .

%. 2, , l = 0 , x ≡ x0 ,

,

.

. & :

A x + B1 y + C1 z + D1 = 0

(10.1)

1

,

A2 x + B2 y + C2 z + D2 = 0

n = ( A1 , B , C1 ) − π1 ,

n2 = ( A2 , B2 , C2 ) - π 2 .

1

( π1

π 2

( ).

" , n1 n2

, . .

[n1 , n2 ] ≠ 0 . ' a = [n1 , n2 ] a n1 , a n2 .

a

" π π

= l , l n ,

l n , a l

≠ 0 .

π 2

1

2

1

2

a l .

l

a

π1

4 " .

24

§11.

" ,

( 1) (

1). $"

. y

	:									y2
						y = kx + b , k = tgϕ -
	I. :									y1
	#		, ϕ -						ϕ	x
	Ox .
										o x1 x2
	( , (x1 , y1 ) (x2 , y2 ) ,
	tgϕ =	y2 − y1	=	kx2 + b − kx1 − b	= k		x2 − x1	= k ),
		x2 − x1		x2 − x1			x2 − x1

b – )) !, Oy. $ , M 0 (x0 y0 ) :

	y − y0 = k (x − x0 )	,	k - ) !.
, M 0 (x0 , y0 ) :									y − y0 = k (x − x0 )	, – .
%. , :
x = x0 , k = ∞ .
II. ' :
				n = ( A, B) l,
	n				n		≠ 0 , n l (
				).
				" n = ( A, B) - l, :
	M 0		x
							A(x − x0 ) + B( y − y0 ) = 0		-

ln , M 0 (x0 , y0 ) .

$ , C = − Ax0 − By0 :

: Ax + By + C = 0 , A2 + B2 ≠ 0 & .

: , :

Ax + By + C = 0 , A2 + B2 ≠ 0 ,

n = ( A, B) - . III. 1 :

	y		" n - l,
				n		= 1 n = {cosα , sin α} ( sin α = cos (π 2 − α )
		M1	n(cosα , cos (π 2 − α )) ).
	r	M0	% .
			$ OM 0 l, OM 0				= r
	n		M 0 (r cosα , r sin α ) .
	α
	o		x

l

25

% cosα (x − r cosα ) + sin α ( y − r sin α ) = 0 , :

x cosα + y sin α − r = 0	- ,

α - Ox, r = dist(O, l) .

#

" M1 (x1 , y1 ) .

. l δ = δ (M1 , l) = µn M 0 M1 .

:

1.δ = dist(M1 , l)

2.	δ > 0				M1					O																					.
3.	δ < 0				M1					O .
* :																	δ = δ (M1 , l) = x1 cosα + y1 sin α − r																														.
* M1 (x1 , y1 )																																														Ax + By + C = 0 :
										δ = dist(M1 , l) =															Ax1						+ By1 + C										.
																														A2 + B2
.
": 2x − 3 y + 5 = 0																	~			2				x −						3			y +		5					= 0			~
																				13										13					13
~ -	2			x +			3		y −			5					= 0			- .
	13				13					13
" M				(1, 2) , δ = δ (M l) = -																							2					1 +			3				2 −				5			= −			1		. ':
	1																			1							13								13								13			13
																	1						1
1)			d = dist(M							, l) =			−							=							;
									1								13						13
2)			M1		O .
IV.		" :																																																			a		= 0, a l .
	y																	a - l,

n" M 0 (x0 , y0 ) l a = (a1 , a2 ) -

l. (:

a			x = x0	+ a1t
M 0	(x0 , y0 , z0 )
		x		t R .
			y = y0	+ a2t
o
	l
V. 4 :
/ t , :						x − x0	=	y − y0
						a1		a2

- l, M 0 (x0 , y0 )

a = (a1 , a2 ) .

26

4 :
	x − x0		y − y0
		=		~	a (x − x ) − a ( y − y ) = 0				- n(a , −a ) ,
	a1				2	0	1	0		2	1
			a2

a n, . (a, n)=a1a2 − a2 a1 = 0 .

+ IV. . (

$ (x, y) .

Ax + By + C = 0 , A2 + B2 ≠ 0 .

%: Ax2 + 2Bxy + Cy2 + 2Dx + 2Ey + F = 0 , A2 + B2 + C 2 ≠ 0 ?

. : , , , .

., ,

5 (2-3 . & . .)

0

4

,

4 ( ) ,

, - ) F

) d .

α

F d : M ( ) ,

M

= const = ε .

MF

M0

MM

0

F

%, ε M . :

F –

,

d – ,

ε – #.

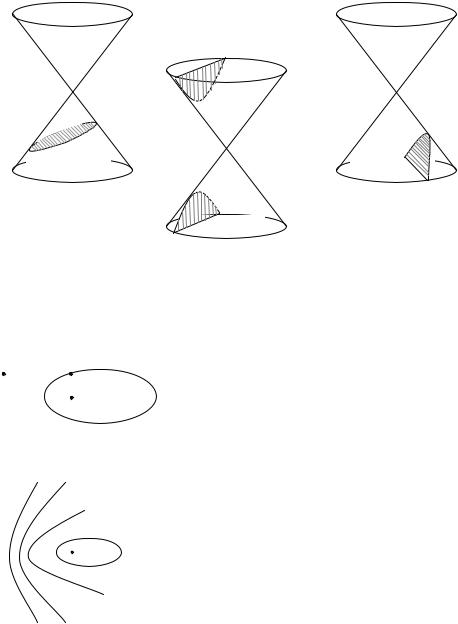
ε > 1

ε = 1

',

ε < 1

# ( ),

F

0 < ε < 1

ε = 1

( ),

ε > 1

(").

α

27

§12.

+ :

0 ,

F1 F2

.

y

:

M (x, y)

:

r1

F1 (−c, 0)

r2

#

,

x

F2 (c, 0)

F1

F2

2 – ) ,

r1 =

F1M

,

r2 =

F2 M

.

" M – , M (x, y) , :

r1 + r2 = const = 2a ( M).

2a -

:

r1 + r2 =

2a

2a > 2c, a > c ( )

" :

r = (x + c)2 + y2

, r = (x − c)2

+ y2

1

2

(x + c)2 + y2 + (x − c)2 + y2 = 2a

(x + c)2 + y2 = 4a2 − 4a (x − c)2 + y2 + y2 + (x − c)2

x2 + 2xc + c2 + y2 = 4a2 − 4a (x − c)2 + y2 + y2 + x2 + c2 − 2xc

a (x − c)2 + y2 = a2 − cx

a2 (x − c)2 + a2 y2 = a4 − 2a2cx + c2 x2

a2 x2 − 2a2 xc + a2c2 + a2 y2 = a4 − 2a2cx + c2 x2

x2 (a2 − c2 ) + a2 y2 = a2 (a2 − c2 )

x2

+

y2

= 1 ,

b2

= a2 − c2 (> c) .

a2

a2

− c2

" #.

x2

+

y2

= 1

, b2 = a2 − c2

.

(12.1)

a2

b2

&, . ", - (12.1) .

$ (12.1), b ≤ a . ' c = a2 − b2 $ ) F1 (−c, 0) F2 (c, 0) .

M (x, y) , (12.1).

x2 = a2 (1−

y2

)

x

2

≤

a

2

(x2 ≤ a2 )

x

≤

a

= a .

b2

= b2 (1−

x2

) = (a2 − c2 )(1−

x2

y2

)

a2

a2

(x ± c)2 + (a2 − c2 )(1−

x2

)

= x2 ± 2xc + c2 + a2 − x2 − c2 +

c2 x2

r = (x ± c)2 + y2 =

=

a2

1,2

a2

28

c2 x2

x

= a2 ± 2xc +

= (a ±

cx

)2 = a ±

cx

( . .

cx

≤

c

≤

c

= c < a ).

a2

a

a

a

a

r + r = a +

cx

+ a −

cx

= 2a

1

2

a

a

", M (x, y) , (12.1),

.

(: + , r1 + r2 = 2a ) F1 (−c, 0) F2 (c, 0)

,

:

y

x

2

+

y

2

= 1 , b2 = a2 − c2

b

a2

b2

M ''

M

a – - ,

b – .

−a

x 2 M (x, y)

,

a

M (−x, y) , M (x, − y)

M (−x, − y)

F2

F1

, ,

M '''

M '

−b

(a, 0)

.

(−a, 0)

c = a2 − b2 - ) F

(0, b) #

2

(0, −b)

ε =

c

- !

x = ±

a

= ±

a2

-

a

ε

c

& 0 ≤ ε ≤ 1:

ε = 0 c = 0 .

ε = 1−

b2

→ 1

b

→ 0

Ox.

a2

a

3 # " ".

	$	x2	+	y2	= 1, 0 < a < b .
		a2		b2

% x y . " , Oy )

F (−c, 0)

F (c, 0) , c = b2 − a2

1

2

.

Ax2 + By2 = C A,B C

( , A = B ).

&.

Ax2 + By2 = C ~

A

x2 +

B

y2 = 1 ~

C

C

x2

y2

x2

y2

~

+

= 1

~

+

= 1, a =

C

, b =

C

.

C A

C B

a2

b2

A

B

" ( a = b

A = B ).

29

§13.

" F1 F2 - ) .

, ,

F1 F2 .

y

M ( x, y)

r1

r2

F1 (−c, 0)

F2 (c, 0)

:

F1 F2 - ) ,

2 – ) , M (x, y) - ,

xr1 = MF1 , r2 = MF2 .

+ : r1 − r2 = 2a ,

– ) ( ) % 2a < 2c ( )

r = (x + c)2 + y2

, r = (x − c)2 + y2

1

2

= ±2a ( )

(x + c)2 + y2 −

(x − c)2 + y2

x2

+

y2

= 1 ~

x2

−

y2

= 1 .

a2

a2

− c2

c2 − a2

a2

/:

x2

−

y2

= 1,

b2

= c2 − a2

– .

(13.1).

a2

b2

5 , , (13.1),

.

(: +

r1 − r2

= 2a ) F1 (−c, 0) F2 (c, 0)

,

(13.1).

x2

−

y2

= 1,

= c2 − a2

%. 2

b2

, c = a2 + b2 .

a2

b2

: " .

" (13.1):

2 M (x, y) , M (−x, y) , M (x, − y)

M (−x, − y)

.

y

. 8 )

.

−a

a

x

& ) I

( x ≥ 0, y ≥ 0) .

y = b −1+ x2

a2

' : 2 x ≥ a , ) ! x → +∞ .

",

y = ±

b

x

:

a

b2

x2 − b2 −

b2

x2

x

2

b

a2

a2

y

− y

= b

−1 −

x =

=

2

a

a

x

2

b

b

−1 +

x

a2

a

30