20. Смо с произвольными потоками событий. Случай бесприоритетной дисциплины обслуживания.

Идея метода вложенных цепей Маркова – в случайном процессе рассматриваются моменты времени, в которые можно рассматривать процесс, как марковский. Можно принимать такие моменты времени за моменты времени поступления заявок.

Q(t) – объем незавершенной работы системы. Необходимо оценить время, которое требуется для завершения этого объема работы.

Имеем СМО с непрерывными состояниями, работающую в непрерывном времени, но имеющую разрывы (будут рассмотрены периоды t).

Рассмотрим одноканальную разомкнутую СМО с неограниченной очередью. На вход системы поступают заявки H типов, считаем, что заявки каждого из H типов образуют простейший поток. Известны интенсивности: . Суммарный поток тоже будет простейшим: .

Принципиально: потоки обслуживания H типов имеют произвольное распределение.

Кодификатор: M|G|1|∞|∞

Для времен обслуживания заявок каждого из H типов известно:

1. 

2. 

К потокам с произвольным распределением теорию марковских процессов применить нельзя.

Вероятность того, что пришедшая на вход заявка является заявкой i-того типа:

Среднее время ожидания заявки произвольного типа (среднее среднего):

В данном случае можно использовать формулу Литтла, так как СМО разомкнута, а очередь неограниченна.

Среднее время пребывания заявки в системе:

Среднее время обслуживания заявок произвольного типа:

R ~ вероятность застать канал занятым обслуживанием заявки какого-либо типа.

– среднее число каналов, занятых обслуживанием заявок i-того типа. Канал один => доля занятости канала.

Коэффициент загрузки

Предположим, что в момент времени t приходит заявка i-того типа. t->З_i.

Тогда время ожидания обслуживания:

– время ожидания обслуживания заявки i-того типа, если канал свободен и очередь пустая (в нашем случае = 0, то есть заявка сразу поступает на обслуживание).

– время ожидания обслуживания вновь пришедшей заявки, когда канал обслуживания занят обслуживанием ранее пришедшей заявки, а в очереди – l заявок j-того типа.

Случай 1: бесприоритетная дисциплина ожидания и обслуживания.

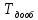– дообслуживание ранее пришедшей заявки, находящейся в канале.

– время обслуживания всех заявок, находящихся в очереди, пришедших в систему до момента времени t.

Из первых H-1 уравнений вычтем последнее H’тое:

То есть при использовании бесприоритетных дисциплин ожидания и обслуживания в среднем время ожидания заявки любого типа одинаково.

Определим среднее время дообслуживания заявок.

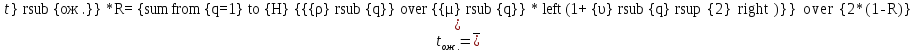
Границы:

1. Если поток регулярный, то длительность обслуживания постоянна, дисперсия длительности обслуживания равна нулю, коэффициент вариации равен нулю, => наименьшее время.

2. Если поток простейший, коэффициент вариации равен 1, , то есть в два раза дольше.

3. Условие установившегося режима: R<1, если не выполняется – коэффициент загрузки = 1, растет очередь.

21. Смо с произвольными потоками событий. Случай дисциплины обслуживания с относительным приоритетом.

Идея метода вложенных цепей Маркова – в случайном процессе рассматриваются моменты времени, в которые можно рассматривать процесс, как марковский. Можно принимать такие моменты времени за моменты времени поступления заявок.

Q(t) – объем незавершенной работы системы. Необходимо оценить время, которое требуется для завершения этого объема работы.

Имеем СМО с непрерывными состояниями, работающую в непрерывном времени, но имеющую разрывы (будут рассмотрены периоды t).

Рассмотрим одноканальную разомкнутую СМО с неограниченной очередью. На вход системы поступают заявки H типов, считаем, что заявки каждого из H типов образуют простейший поток. Известны интенсивности: . Суммарный поток тоже будет простейшим: .

Принципиально: потоки обслуживания H типов имеют произвольное распределение.

Кодификатор: M|G|1|∞|∞

--------------------------------------------------------

Рассмотрим СМО с бесприоритетной дисциплиной ожидания и дисциплиной обслуживания с относительным приоритетом (без прерывания обслуживания).

Пусть число приоритетов N совпадает с числом типов заявок H.

Pr = 1,2,…, N. Будем считать, что самый высокий приоритет – под номером 1.

N = H.

Будем считать, что для каждого типа заявок используется индивидуальная очередь, количество мест очереди не ограничено.

Загрузка заявок в канал обслуживания – с самым высоким приоритетом (но прерывания не происходит).

Если канал занят обслуживанием, то пришедшая заявка занимает последнее место в очереди заявок своего приоритета.

– время ожидания обслуживания ранее пришедших заявок с уровнем приоритета k и выше.

– ожидание обслуживания заявок, пришедших за время обслуживания и имеющих более высокий приоритет.

– дообслуживание заявки, находящийся в канале.

– обслуживание заявок, которые к моменту t уже стояли в очередях с приоритетом k и выше.

Эти две величины являются составными частями .

Усредним равенство:

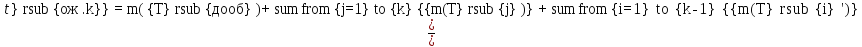
Для k = 1 (самый высокий приоритет):

Для k = 2:

Для общего случая по индукции:

Если рассмотреть разность времен ожидания k-того и k-1 приоритета, то станет видно, что с увеличением приоритета время ожидания уменьшается. Таким образом, введение относительного приоритета приводит к уменьшению среднего времени ожидания высокоприоритетных заявок и к увеличению среднего времени ожидания низкоприоритетных заявок.