EP / Теория ЭП Драчев

Ɇɨɦɟɧɬ ɢɧɟɪɰɢɢ ɯɨɞɨɜɨɝɨ ɜɢɧɬɚ

m

§dCP ·2

§0,044

·2

2

JXB

¨

¸

100 ¨

¸

0,0484 ɤɝ ɦ

.

2

© 2

¹

©

¹

Ɇɨɦɟɧɬ ɢɧɟɪɰɢɢ ɪɚɛɨɱɟɝɨ ɨɪɝɚɧɚ

J

J

J

XB

0,0106 0,0484

0,059 ɤɝ ɦ2 .

PO

C

Ɇɨɦɟɧɬ ɢɧɟɪɰɢɢ ɪɚɛɨɱɟɝɨ ɨɪɝɚɧɚ, ɩɪɢɜɟɞɟɧɧɵɣ ɤ ɜɚɥɭ ɞɜɢɝɚɬɟɥɹ,

JɉɊ	JPO			0,059	0,00236	ɤɝ ɦ	2	.
	i	2	52
	12

Ɇɨɦɟɧɬ ɢɧɟɪɰɢɢ ɩɟɪɟɞɚɱɢ, ɩɪɢɜɟɞɟɧɧɵɣ ɤ ɜɚɥɭ ɞɜɢɝɚɬɟɥɹ,

J	J		J2	0,03	0,6	0,054 ɤɝ ɦ2 .
		i
ɉȿɊ	1		2	52
		12

Ʉɨɷɮɮɢɰɢɟɧɬ, ɭɱɢɬɵɜɚɸɳɢɣ ɦɨɦɟɧɬ ɢɧɟɪɰɢɢ ɩɟɪɟɞɚɱɢ ɜ ɦɨɦɟɧɬɟ ɢɧɟɪɰɢɢ ɪɨɬɨɪɚ ɞɜɢɝɚɬɟɥɹ,

į	JȾȼ JɉȿɊ	0,2 0,054 1,27 .
	JȾȼ	0,2

ɋɭɦɦɚɪɧɵɣ ɦɨɦɟɧɬ ɢɧɟɪɰɢɢ ɦɟɯɚɧɢɱɟɫɤɨɣ ɱɚɫɬɢ

J į JȾȼ JɉɊ 1,27 0,2 0,00236 0,256 ɤɝ ɦ2 .

2.4. ɍɪɚɜɧɟɧɢɟ ɞɜɢɠɟɧɢɹ ɷɥɟɤɬɪɨɩɪɢɜɨɞɚ

Ɇɟɯɚɧɢɱɟɫɤɚɹ ɷɧɟɪɝɢɹ ɧɚ ɜɚɥɭ ɞɜɢɝɚɬɟɥɹ WȾȼ ɪɚɫɯɨɞɭɟɬɫɹ:

–ɧɚ ɫɨɜɟɪɲɟɧɢɟ ɩɨɥɟɡɧɨɣ ɪɚɛɨɬɵ ɢ ɩɪɟɨɞɨɥɟɧɢɟ ɫɨɩɪɨɬɢɜɥɟɧɢɹ ɞɜɢɠɟɧɢɸ ɪɚɛɨɱɟɝɨ ɨɪɝɚɧɚ WC ;

–ɧɚ ɫɨɡɞɚɧɢɟ ɡɚɩɚɫɚ ɤɢɧɟɬɢɱɟɫɤɨɣ ɷɧɟɪɝɢɢ ɜ ɦɟɯɚɧɢɱɟɫɤɨɣ ɱɚɫɬɢ ɷɥɟɤɬɪɨɩɪɢɜɨɞɚ WɄɂɇ

					WȾȼ		Wɋ WɄɂɇ .		(2.22)
Ɇɨɳɧɨɫɬɶ ɞɜɢɝɚɬɟɥɹ ɪɚɜɧɚ ɩɪɨɢɡɜɨɞɧɨɣ ɷɧɟɪɝɢɢ ɩɨ ɜɪɟɦɟɧɢ
	dWȾȼ		dW			dW
			C			Ʉɂɇ		Ɋɋ ɊȾɂɇ Ɇɋ Ȧ ɆȾɂɇ Ȧ.	(2.23)
ɊȾȼ	dt
			dt			dt
Ɍɨɝɞɚ ɦɨɦɟɧɬ ɞɜɢɝɚɬɟɥɹ
						Ɇ	Ɇɋ ɆȾɂɇ.		(2.24)

Ɉɩɪɟɞɟɥɢɦ ɞɢɧɚɦɢɱɟɫɤɢɣ ɦɨɦɟɧɬ, ɩɪɨɞɢɮɮɟɪɟɧɰɢɪɨɜɚɜ ɩɨ ɜɪɟɦɟɧɢ ɜɵɪɚɠɟɧɢɟ ɤɢɧɟɬɢɱɟɫɤɨɣ ɷɧɟɪɝɢɢ:

§

J Ȧ2 ·

d

¨

¸

¨

2

¸

2

dJ

dȦ

(2.25)

dWɄɂɇ

©

¹

Ȧ

J Ȧ

PȾɂɇ

ɆȾɂɇ Ȧ.

dt

dt

2

dt

dt

21

ɂɡ ɮɨɪɦɭɥɵ (2.25) ɫɥɟɞɭɟɬ, ɱɬɨ ɞɢɧɚɦɢɱɟɫɤɢɣ ɦɨɦɟɧɬ

	Ȧ		dJ	J	dȦ	.	(2.26)
ɆȾɂɇ
	2 dt				dt

Ɇɨɦɟɧɬ Ɇ, ɪɚɡɜɢɜɚɟɦɵɣ ɞɜɢɝɚɬɟɥɟɦ, ɭɪɚɜɧɨɜɟɲɢɜɚɟɬɫɹ ɦɨɦɟɧɬɨɦ ɫɨɩɪɨɬɢɜɥɟɧɢɹ ɞɜɢɠɟɧɢɸ MC ɢ ɞɢɧɚɦɢɱɟɫɤɢɦ ɦɨɦɟɧɬɨɦ ɆȾɂɇ:

Ɇ Ɇɋ ɆȾɂɇ			Ȧ		dJ	J	dȦ	.	(2.27)
	Ɇɋ
			2 dt				dt

ȼɵɪɚɠɟɧɢɟ (2.27) ɧɚɡɵɜɚɸɬ ɩɨɥɧɵɦ ɭɪɚɜɧɟɧɢɟɦ ɞɜɢɠɟɧɢɹ.

Ⱦɥɹ ɛɨɥɶɲɢɧɫɬɜɚ ɦɟɯɚɧɢɡɦɨɜ ɦɨɦɟɧɬ ɢɧɟɪɰɢɢ J = const. Ɍɨɝɞɚ ɩɨɥɭɱɚɟɦ ɨɫɧɨɜɧɨɟ ɭɪɚɜɧɟɧɢɟ ɞɜɢɠɟɧɢɹ ɷɥɟɤɬɪɨɩɪɢɜɨɞɚ:

	J	dȦ	.	(2.28)
Ɇ Ɇɋ
		dt

ȼ ɨɫɧɨɜɧɨɟ ɭɪɚɜɧɟɧɢɟ ɞɜɢɠɟɧɢɹ ɜɯɨɞɹɬ:

– Ɇ – ɷɥɟɤɬɪɨɦɚɝɧɢɬɧɵɣ ɦɨɦɟɧɬ ɞɜɢɝɚɬɟɥɹ;

–Ɇɋ – ɦɨɦɟɧɬ ɫɨɩɪɨɬɢɜɥɟɧɢɹ ɞɜɢɠɟɧɢɸ, ɨɛɟɫɩɟɱɢɜɚɸɳɢɣ ɩɪɟɨɞɨɥɟɧɢɟ ɦɨɦɟɧɬɨɜ ɢ ɫɢɥ ɫɨɩɪɨɬɢɜɥɟɧɢɹ ɞɜɢɠɟɧɢɸ. ȼ ɞɚɥɶɧɟɣɲɟɦ Ɇɋ ɛɭɞɟɦ ɧɚɡɵɜɚɬɶ

ɫɬɚɬɢɱɟɫɤɢɦ ɦɨɦɟɧɬɨɦ, ɞɟɣɫɬɜɭɸɳɢɦ ɜ ɫɬɚɬɢɤɟ ɢ ɞɢɧɚɦɢɤɟ;

– ɆȾɂɇ – ɞɢɧɚɦɢɱɟɫɤɢɣ ɦɨɦɟɧɬ, ɞɟɣɫɬɜɭɸɳɢɣ ɬɨɥɶɤɨ ɜ ɞɢɧɚɦɢɤɟ. Ɉɫɧɨɜɧɨɟ ɭɪɚɜɧɟɧɢɟ ɞɜɢɠɟɧɢɹ ɩɨɡɜɨɥɹɟɬ ɨɰɟɧɢɬɶ ɫɨɫɬɨɹɧɢɟ, ɜ ɤɨɬɨɪɨɦ

ɧɚɯɨɞɢɬɫɹ ɷɥɟɤɬɪɨɩɪɢɜɨɞ:

– ɩɪɢ Ɇ > Ɇɋ

J

dȦ

! 0 ɩɪɢ J = const

dȦ

! 0

ȦĹ – ɷɥɟɤɬɪɨɩɪɢɜɨɞ

dt

dt

ɪɚɡɝɨɧɹɟɬɫɹ;

– ɩɪɢ Ɇ < Ɇɋ

J

dȦ

0 ɩɪɢ J = const

dȦ

0

ȦĻ – ɷɥɟɤɬɪɨɩɪɢɜɨɞ

dt

dt

ɬɨɪɦɨɡɢɬɫɹ;

– ɩɪɢ Ɇ = Ɇɋ

J

dȦ

0 ɩɪɢ J = const

dȦ

0

Ȧ=const – ɫɤɨɪɨɫɬɶ

dt

dt

ɷɥɟɤɬɪɨɩɪɢɜɨɞɚ ɩɨɫɬɨɹɧɧɚ, ɭɫɬɚɧɨɜɢɜɲɢɣɫɹ ɪɟɠɢɦ ɪɚɛɨɬɵ ɷɥɟɤɬɪɨɩɪɢɜɨɞɚ;

	– ɩɪɢ Ɇ = 0 Ɇ		Ɇ		dȦ	<0 ȦĻ – ɷɥɟɤɬɪɨɩɪɢɜɨɞ ɬɨɪɦɨɡɢɬɫɹ
		Ⱦɂɇ		ɋ	dt

ɩɨɞ ɞɟɣɫɬɜɢɟɦ ɫɬɚɬɢɱɟɫɤɨɝɨ ɦɨɦɟɧɬɚ ɩɪɢ ɨɬɤɥɸɱɟɧɧɨɦ ɞɜɢɝɚɬɟɥɟ (ɬɨɪɦɨɠɟɧɢɟ ɧɚ ɜɵɛɟɝɟ).

Ɂɧɚɤɢ ɦɨɦɟɧɬɨɜ:

–ɦɨɦɟɧɬ ɞɜɢɝɚɬɟɥɹ ɩɨɥɨɠɢɬɟɥɶɧɵɣ – Ɇ (+), ɟɫɥɢ ɧɚɩɪɚɜɥɟɧɢɟ ɞɟɣɫɬɜɢɹ ɦɨɦɟɧɬɚ ɞɜɢɝɚɬɟɥɹ ɫɨɜɩɚɞɚɟɬ ɫ ɧɚɩɪɚɜɥɟɧɢɟɦ ɜɪɚɳɟɧɢɹ ɞɜɢɝɚɬɟɥɹ;

–ɫɬɚɬɢɱɟɫɤɢɣ ɦɨɦɟɧɬ ɩɨɥɨɠɢɬɟɥɶɧɵɣ – Ɇɋ (+), ɟɫɥɢ ɫɬɚɬɢɱɟɫɤɢɣ ɦɨɦɟɧɬ

ɧɚɩɪɚɜɥɟɧ ɧɚɜɫɬɪɟɱɭ ɫɤɨɪɨɫɬɢ ɜɪɚɳɟɧɢɹ ɞɜɢɝɚɬɟɥɹ.

Ɉɫɧɨɜɧɨɟ ɭɪɚɜɧɟɧɢɟ ɩɨɫɬɭɩɚɬɟɥɶɧɨɝɨ ɞɜɢɠɟɧɢɹ ɜɵɜɨɞɢɬɫɹ ɚɧɚɥɨɝɢɱɧɨ ɢ ɢɦɟɟɬ ɜɢɞ

FȾȼ F m

dv

,

(2.29)

C dt

ɝɞɟ FȾȼ – ɫɢɥɚ ɞɜɢɝɚɬɟɥɹ (ɥɢɧɟɣɧɨɝɨ);

22

FC – ɫɢɥɚ ɫɨɩɪɨɬɢɜɥɟɧɢɹ ɞɜɢɠɟɧɢɸ;

m – ɩɟɪɟɞɜɢɝɚɟɦɚɹ ɦɚɫɫɚ;

v – ɥɢɧɟɣɧɚɹ ɫɤɨɪɨɫɬɶ ɩɟɪɟɞɜɢɠɟɧɢɹ.

2.5. Ɇɟɯɚɧɢɱɟɫɤɚɹ ɱɚɫɬɶ ɷɥɟɤɬɪɨɩɪɢɜɨɞɚ ɤɚɤ ɨɛɴɟɤɬ ɭɩɪɚɜɥɟɧɢɹ

Ɋɚɫɫɦɨɬɪɢɦ ɪɚɫɱɟɬɧɭɸ ɫɯɟɦɭ ɷɥɟɤɬɪɨɩɪɢɜɨɞɚ ɫ ɛɟɫɤɨɧɟɱɧɨɣ ɠɟɫɬɤɨɫɬɶɸ ɦɟɯɚɧɢɱɟɫɤɢɯ ɫɜɹɡɟɣ ɦɟɠɞɭ ɷɥɟɦɟɧɬɚɦɢ. Ɋɚɫɱɟɬɧɚɹ ɫɯɟɦɚ ɷɥɟɤɬɪɨɩɪɢɜɨɞɚ ɩɪɟɞɫɬɚɜɥɹɟɬɫɹ ɜɪɚɳɚɸɳɢɦɫɹ ɷɥɟɦɟɧɬɨɦ ɫ ɦɨɦɟɧɬɨɦ ɢɧɟɪɰɢɢ, ɩɪɢɜɟɞɟɧɧɵɦ ɤ ɜɚɥɭ

ɞɜɢɝɚɬɟɥɹ, J į JȾȼ JPO iɉȿɊ , ɩɪɢɜɟɞɟɧɧɵɦ ɤ ɜɚɥɭ ɞɜɢɝɚɬɟɥɹ ɫɬɚɬɢɱɟɫɤɢɦ ɦɨɦɟɧɬɨɦ Ɇɋ ɢ ɦɨɦɟɧɬɨɦ ɞɜɢɝɚɬɟɥɹ Ɇ.

Ɉɫɧɨɜɧɨɟ ɭɪɚɜɧɟɧɢɟ ɞɜɢɠɟɧɢɹ ɩɪɢ ɥɢɧɟɣɧɨɣ (J = const) ɤɢɧɟɦɚɬɢɱɟɫɤɨɣ ɰɟɩɢ

	Ɇ Ɇɋ	J	dȦ		(2.30)
			dt
	ɡɚɩɢɲɟɦ ɜ ɨɩɟɪɚɬɨɪɧɨɣ ɮɨɪɦɟ:
	M p MC p J Ȧ p p .				(2.31)

ɉɟɪɟɞɚɬɨɱɧɭɸ ɮɭɧɤɰɢɸ ɦɟɯɚɧɢɱɟɫɤɨɣ ɱɚɫɬɢ ɷɥɟɤɬɪɨɩɪɢɜɨɞɚ, ɧɚ ɜɵɯɨɞɟ ɤɨɬɨɪɨɣ ɪɚɫɫɦɚɬɪɢɜɚɟɦ Ȧ(p), ɧɚ ɜɯɨɞɟ – ɞɢɧɚɦɢɱɟɫɤɢɣ ɦɨɦɟɧɬ

	ɪ		Ɇ ɪ	Ɇ	ɪ	,			(2.32)
MȾɂɇ				ɋ
ɩɨɥɭɱɚɟɦ ɜ ɜɢɞɟ
W p	xȼɕɏ		Ȧ ɪ				1/ J	.	(2.33)
			Ɇ ɪ Ɇɋ ɪ
	ɯȼɏ						p

ɀɟɫɬɤɨɟ ɩɪɢɜɟɞɟɧɧɨɟ ɡɜɟɧɨ ɤɚɤ ɨɛɴɟɤɬ ɭɩɪɚɜɥɟɧɢɹ ɦɨɠɟɬ ɛɵɬɶ ɩɪɟɞɫɬɚɜɥɟɧɨ ɢɧɬɟɝɪɢɪɭɸɳɢɦ ɡɜɟɧɨɦ ɫ ɤɨɷɮɮɢɰɢɟɧɬɨɦ ɭɫɢɥɟɧɢɹ 1/J.

ɋɬɪɭɤɬɭɪɧɚɹ ɫɯɟɦɚ (ɨɫɨɛɚɹ ɮɨɪɦɚ ɡɚɩɢɫɢ ɭɪɚɜɧɟɧɢɣ) ɦɟɯɚɧɢɱɟɫɤɨɣ ɱɚɫɬɢ ɷɥɟɤɬɪɨɩɪɢɜɨɞɚ, ɥɨɝɚɪɢɮɦɢɱɟɫɤɚɹ ɚɦɩɥɢɬɭɞɧɚɹ (ɅȺɏ) ɢ ɩɟɪɟɯɨɞɧɚɹ ɯɚɪɚɤɬɟɪɢɫɬɢɤɢ ɢɡɨɛɪɚɠɟɧɵ ɧɚ ɪɢɫ. 2.9.

1

M Ȧ

Zof

ɤ

J

Mɞɢɧ=const

ɆȾɂɇ

1

Ɇ

J

Ȧ

–

p

Ɇɋ

Ȧ

t

Ɋɢɫ. 2.9. ɋɬɪɭɤɬɭɪɧɚɹ ɫɯɟɦɚ, ɅȺɏ ɢ ɩɟɪɟɯɨɞɧɚɹ ɯɚɪɚɤɬɟɪɢɫɬɢɤɚ

ɦɟɯɚɧɢɱɟɫɤɨɣ ɱɚɫɬɢ ɷɥɟɤɬɪɨɩɪɢɜɨɞɚ

ɉɪɢ ɫɤɚɱɤɟ ɧɚ ɜɯɨɞɟ

MȾɂɇ

ɪ

Ɇ ɪ

Ɇ

ɪ

const

ɢ J = const ɜɵɯɨɞɧɚɹ ɜɟɥɢ-

ɋ

ɱɢɧɚ Ȧ(t) ɛɭɞɟɬ ɧɚɪɚɫɬɚɬɶ ɩɨ ɥɢɧɟɣɧɨɦɭ (ɬɚɤ ɤɚɤ dȦ dt İ

const ) ɡɚɤɨɧɭ ɜ

ɮɭɧɤɰɢɢ ɜɪɟɦɟɧɢ ɨɬ Ȧ = 0 ɞɨ Ȧ

f.

23

ɉɟɪɟɣɞɟɦ ɜ ɭɪɚɜɧɟɧɢɢ (2.28) ɤ ɨɬɧɨɫɢɬɟɥɶɧɵɦ ɟɞɢɧɢɰɚɦ (ɨ.ɟ.).

ɉɪɢɧɢɦɚɟɦ ɡɚ ɛɚɡɨɜɵɟ ɜɟɥɢɱɢɧɵ:

– ɆȻ

Ɇɇ – ɧɨɦɢɧɚɥɶɧɵɣ ɷɥɟɤɬɪɨɦɚɝɧɢɬɧɵɣ ɦɨɦɟɧɬ ɞɜɢɝɚɬɟɥɹ;

–ȦȻ

Ȧ0ɇ – ɫɤɨɪɨɫɬɶ ɢɞɟɚɥɶɧɨɝɨ ɯɨɥɨɫɬɨɝɨ ɯɨɞɚ ɩɪɢ ɧɨɦɢɧɚɥɶɧɨɦ ɧɚɩɪɹ-

ɠɟɧɢɢ ɧɚ ɹɤɨɪɟ ɢ ɧɨɦɢɧɚɥɶɧɨɦ ɬɨɤɟ ɜɨɡɛɭɠɞɟɧɢɹ.

Ɉɫɧɨɜɧɨɟ ɭɪɚɜɧɟɧɢɟ ɞɜɢɠɟɧɢɹ ɜ ɨ.ɟ. ɡɚɩɢɫɵɜɚɟɬɫɹ ɜ ɜɢɞɟ

ɌȾ

d

,

(2.34)

Ȧ

Ɇ

Ɇ

ɋ

dt

J Ȧ0H

– ɦɟɯɚɧɢɱɟɫɤɚɹ ɩɨɫɬɨɹɧɧɚɹ ɜɪɟɦɟɧɢ ɷɥɟɤɬɪɨɩɪɢɜɨɞɚ, ɭɱɢɬɵ-

ɝɞɟ ɌȾ

MH

ɜɚɸɳɚɹ ɢ ɩɪɢɜɟɞɟɧɧɵɣ ɦɨɦɟɧɬ ɢɧɟɪɰɢɢ ɪɚɛɨɱɟɝɨ ɨɪɝɚɧɚ.

ɇɚɥɢɱɢɟ ɜ ɭɪɚɜɧɟɧɢɢ ɌȾ ɫɜɢɞɟɬɟɥɶɫɬɜɭɟɬ ɨ ɡɚɩɢɫɢ ɭɪɚɜɧɟɧɢɹ ɜ ɨ.ɟ.

2.6. ɉɟɪɟɯɨɞɧɵɟ ɩɪɨɰɟɫɫɵ ɦɟɯɚɧɢɱɟɫɤɨɣ ɱɚɫɬɢ

ɷɥɟɤɬɪɨɩɪɢɜɨɞɚ

Ɋɚɫɫɦɨɬɪɢɦ ɦɟɯɚɧɢɱɟɫɤɢɟ ɩɟɪɟɯɨɞɧɵɟ ɩɪɨɰɟɫɫɵ, ɜ ɤɨɬɨɪɵɯ ɭɱɢɬɵɜɚɟɬɫɹ ɢɡɦɟɧɟɧɢɟ ɬɨɥɶɤɨ ɤɢɧɟɬɢɱɟɫɤɨɣ ɷɧɟɪɝɢɢ ɦɟɯɚɧɢɱɟɫɤɨɣ ɱɚɫɬɢ ɷɥɟɤɬɪɨɩɪɢɜɨɞɚ. ȼ ɪɟɡɭɥɶɬɚɬɟ ɪɚɫɱɟɬɚ ɧɟɨɛɯɨɞɢɦɨ ɩɨɥɭɱɢɬɶ ɡɚɤɨɧ ɢɡɦɟɧɟɧɢɹ ɫɤɨɪɨɫɬɢ Ȧ(t) ɩɪɢ ɡɚɞɚɧɧɨɦ ɡɚɤɨɧɟ ɢɡɦɟɧɟɧɢɹ ɦɨɦɟɧɬɚ Ɇ(t). Ⱦɥɹ ɩɨɥɭɱɟɧɢɹ ɧɚɝɪɭɡɨɱɧɨɣ ɞɢɚɝɪɚɦɦɵ Ȧ(t) ɪɟɲɚɟɦ ɨɫɧɨɜɧɨɟ ɭɪɚɜɧɟɧɢɟ ɞɜɢɠɟɧɢɹ ɷɥɟɤɬɪɨɩɪɢɜɨɞɚ ɨɬɧɨɫɢɬɟɥɶɧɨ ɫɤɨɪɨɫɬɢ:

M M J	dȦ	.	(2.35)
C	dt
Ɍɚɤ ɤɚɤ ɦɨɦɟɧɬ ɞɜɢɝɚɬɟɥɹ ɱɚɳɟ ɜɫɟɝɨ ɡɚɜɢɫɢɬ ɨɬ ɫɤɨɪɨɫɬɢ			Ɇ(Ȧ), ɦɨɦɟɧɬ

ɫɬɚɬɢɱɟɫɤɢɣ – ɨɬ ɫɤɨɪɨɫɬɢ, ɜɪɟɦɟɧɢ, ɭɝɥɚ ɩɨɜɨɪɨɬɚ ɜɚɥɚ ɪɚɛɨɱɟɝɨ ɨɪɝɚɧɚ MC Ȧ,t,D , ɦɨɦɟɧɬ ɢɧɟɪɰɢɢ – ɨɬ ɫɤɨɪɨɫɬɢ, ɜɪɟɦɟɧɢ, ɭɝɥɚ ɩɨɜɨɪɨɬɚ ɜɚɥɚ ɪɚɛɨ-

ɱɟɝɨ ɨɪɝɚɧɚ J Ȧ,t,D , ɬɨ ɪɟɲɟɧɢɟ ɭɪɚɜɧɟɧɢɹ ɜ ɨɛɳɟɦ ɜɢɞɟ ɧɟɜɨɡɦɨɠɧɨ ɜ ɫɜɹɡɢ ɫ ɨɬɫɭɬɫɬɜɢɟɦ ɭɤɚɡɚɧɧɵɯ ɚɧɚɥɢɬɢɱɟɫɤɢɯ ɡɚɜɢɫɢɦɨɫɬɟɣ. ȿɫɥɢ ɩɪɢɧɹɬɶ, ɱɬɨ Ɇ = const, MC const , J const , ɬɨ ɭɝɥɨɜɨɟ ɭɫɤɨɪɟɧɢɟ

	M MC	const
İ
	J

ɢ ɜ ɩɪɢɧɹɬɵɯ ɭɫɥɨɜɢɹɯ ɫɤɨɪɨɫɬɶ ɜɨ ɜɪɟɦɟɧɢ ɛɭɞɟɬ ɢɡɦɟɧɹɬɶɫɹ ɩɨ ɥɢɧɟɣɧɨɦɭ ɡɚɤɨɧɭ

Ȧ t

ȦɇȺɑ İ t .

(2.36)

Ɋɟɲɟɧɢɟ ɨɫɧɨɜɧɨɝɨ ɭɪɚɜɧɟɧɢɹ ɞɜɢɠɟɧɢɹ ɷɥɟɤɬɪɨɩɪɢɜɨɞɚ ɜ ɨ.ɟ.

d

M

M

Ȧ

Ɍ

C

Ⱦ

dt

24

ɞɥɹ M

const , MC const , J const ɩɪɢɧɢɦɚɟɬ ɜɢɞ

t

M

M

M

M

C

dt

C

ǻt ȦɇȺɑ

,

(2.37)

Ȧ

0³

ɌȾ

ɌȾ

ɋ

.

Ɇ

Ɇ

ɝɞɟ İ

ɌȾ

ȼɪɟɦɹ ɩɟɪɟɯɨɞɧɨɝɨ ɩɪɨɰɟɫɫɚ ɦɨɠɧɨ ɪɚɫɫɱɢɬɚɬɶ ɢɡ ɨɫɧɨɜɧɨɝɨ ɭɪɚɜɧɟɧɢɹ ɞɜɢɠɟɧɢɹ

t

J

dȦ.

t

³

(2.38)

M M

0

C

Ⱦɥɹ Ɇ = const, MC const , J

const

ǻt

J

(ȦɄɈɇ

ȦɇȺɑ) .

(2.39)

M MC

ȼɪɟɦɹ ɩɟɪɟɯɨɞɧɨɝɨ ɩɪɨɰɟɫɫɚ ɜ ɨ.ɟ. ɦɨɠɧɨ ɨɩɪɟɞɟɥɢɬɶ ɩɨ ɮɨɪɦɭɥɟ

ǻt

ɌȾ ǻȦ

.

(2.40)

M MC

Ɍɚɤɢɦ ɨɛɪɚɡɨɦ, ɜɪɟɦɹ ɩɟɪɟɯɨɞɧɨɝɨ ɩɪɨɰɟɫɫɚ ɩɪɹɦɨ ɩɪɨɩɨɪɰɢɨɧɚɥɶɧɨ ɌȾ ɢ

ɨɛɪɚɬɧɨ ɩɪɨɩɨɪɰɢɨɧɚɥɶɧɨ ɜɟɥɢɱɢɧɟ ɞɢɧɚɦɢɱɟɫɤɨɝɨ ɦɨɦɟɧɬɚ ɆȾɂɇ				Ɇ Ɇɋ.
ȿɫɥɢ ɪɚɫɫɦɨɬɪɟɬɶ ɩɭɫɤ ɞɜɢɝɚɬɟɥɹ ɧɚ ɯɨɥɨɫɬɨɦ ɯɨɞɭ ɩɪɢ Ɇ			Ɇɇ, Ɇɋ 0 ,
ȦɇȺɑ 0 , ȦɄɈɇ Ȧ0ɇ, ɬɨɝɞɚ ǻȦ Ȧ0ɇ ɢ ɜɪɟɦɹ ɩɟɪɟɯɨɞɧɨɝɨ ɩɪɨɰɟɫɫɚ ɩɨ ɮɨɪ-

ɦɭɥɟ (2.39) ɛɭɞɟɬ ɪɚɜɧɨ ɦɟɯɚɧɢɱɟɫɤɨɣ ɩɨɫɬɨɹɧɧɨɣ ɜɪɟɦɟɧɢ ɷɥɟɤɬɪɨɩɪɢɜɨɞɚ

ǻt	J ǻȦ		J Ȧ0ɇ	ɌȾ .
	M MC MH

Ɉɬɫɸɞɚ ɜɢɞɟɧ ɮɢɡɢɱɟɫɤɢɣ ɫɦɵɫɥ ɌȾ:

Ɇɟɯɚɧɢɱɟɫɤɚɹ ɩɨɫɬɨɹɧɧɚɹ ɜɪɟɦɟɧɢ ɷɥɟɤɬɪɨɩɪɢɜɨɞɚ ɌȾ ɟɫɬɶ ɜɪɟɦɹ, ɜ ɬɟɱɟɧɢɟ ɤɨɬɨɪɨɝɨ ɞɜɢɝɚɬɟɥɶ ɫ ɦɨɦɟɧɬɨɦ ɢɧɟɪɰɢɢ J ɪɚɡɝɨɧɢɬɫɹ ɧɚ ɯɨɥɨɫɬɨɦ ɯɨɞɭ ɢɡ ɧɟɩɨɞɜɢɠɧɨɝɨ ɫɨɫɬɨɹɧɢɹ ɞɨ ɫɤɨɪɨɫɬɢ ɢɞɟɚɥɶɧɨɝɨ ɯɨɥɨɫɬɨɝɨ ɯɨɞɚ ɩɨɞ ɞɟɣɫɬɜɢɟɦ ɦɨɦɟɧɬɚ, ɪɚɜɧɨɝɨ ɧɨɦɢɧɚɥɶɧɨɦɭ.

ɍɝɨɥ ɩɨɜɨɪɨɬɚ ɜɚɥɚ ɞɜɢɝɚɬɟɥɹ ɡɚ ɜɪɟɦɹ ɩɟɪɟɯɨɞɧɨɝɨ ɩɪɨɰɟɫɫɚ ɪɚɫɫɱɢɬɵɜɚɟɬɫɹ ɞɥɹ ɨɩɪɟɞɟɥɟɧɢɹ ɩɟɪɟɦɟɳɟɧɢɹ ɪɚɛɨɱɟɝɨ ɨɪɝɚɧɚ, ɫɜɹɡɚɧɧɨɝɨ ɫ ɜɚɥɨɦ ɞɜɢɝɚɬɟɥɹ ɤɢɧɟɦɚɬɢɱɟɫɤɨɣ ɰɟɩɶɸ.

ɉɪɢɪɚɳɟɧɢɟ ɭɝɥɚ ɩɨɜɨɪɨɬɚ ǻĮ ɡɚ ɜɪɟɦɹ ǻt ɨɩɪɟɞɟɥɹɟɬɫɹ ɭɝɥɨɜɨɣ ɫɤɨɪɨɫɬɶɸ

Ȧ	dĮ		ǻĮ	,	(2.41)
	dt
			ǻt

ɨɬɤɭɞɚ ǻĮ Ȧ t ǻt .

ȿɫɥɢ Ȧ(t) = const, ɬɨ ǻĮ = Ȧ·ǻt.

ȿɫɥɢ ɮɭɧɤɰɢɹ Ȧ(t) – ɥɢɧɟɣɧɚɹ, ɬɨ Į ³Ȧ dt İ t2 .

2

25

ɉɪɢ ɧɟɥɢɧɟɣɧɨɣ ɮɭɧɤɰɢɢ Ȧ(t) ɱɚɳɟ ɜɫɟɝɨ ɷɬɭ ɡɚɜɢɫɢɦɨɫɬɶ ɪɚɡɛɢɜɚɸɬ ɧɚ ɥɢɧɟɣɧɵɟ ɭɱɚɫɬɤɢ ɢ ǻĮ ɪɚɫɫɱɢɬɵɜɚɸɬ ɩɨ ɭɱɚɫɬɤɚɦ ɤɚɤ ɥɢɧɟɣɧɭɸ ɮɭɧɤɰɢɸ

	ǻt	ȦɇȺɑ ȦɄɈɇ	ǻt .	(2.42)
ǻĮ ȦCP
	2

Ɉɩɬɢɦɚɥɶɧɨɟ ɩɟɪɟɞɚɬɨɱɧɨɟ ɱɢɫɥɨ ɪɟɞɭɤɬɨɪɚ [14] ɩɨɥɭɱɚɸɬ ɢɡ ɭɫɥɨɜɢɹ ɨɛɟɫɩɟɱɟɧɢɹ ɦɢɧɢɦɚɥɶɧɨɝɨ ɜɪɟɦɟɧɢ ɩɟɪɟɯɨɞɧɨɝɨ ɩɪɨɰɟɫɫɚ ɪɚɛɨɱɟɝɨ ɨɪɝɚɧɚ. ɉɪɢ ɢɡɦɟɧɟɧɢɢ ɩɟɪɟɞɚɬɨɱɧɨɝɨ ɱɢɫɥɚ ɪɟɞɭɤɬɨɪɚ iP ɩɪɢ ɨɞɧɢɯ ɢ ɬɟɯ ɠɟ ɞɜɢɝɚ-

ɬɟɥɟ ɢ ɪɚɛɨɱɟɦ ɨɪɝɚɧɟ ɢɡɦɟɧɹɟɬɫɹ ɢ ɫɨɨɬɧɨɲɟɧɢɟ ɦɟɠɞɭ ɫɤɨɪɨɫɬɹɦɢ ɢ ɭɫɤɨɪɟɧɢɹɦɢ ɞɜɢɝɚɬɟɥɹ ɢ ɪɚɛɨɱɟɝɨ ɨɪɝɚɧɚ.

M iP MPO	JȾȼ	iP2 JPO		dȦPO	.	(2.43)
				dt

Ɂɚɩɢɲɟɦ ɨɫɧɨɜɧɨɟ ɭɪɚɜɧɟɧɢɟ ɞɜɢɠɟɧɢɹ ɞɥɹ ɪɚɛɨɱɟɝɨ ɨɪɝɚɧɚ, ɩɪɢɧɢɦɚɹ ɄɉȾ ɪɟɞɭɤɬɨɪɚ ȘP 1.

Ɋɟɲɚɹ (2.43) ɨɬɧɨɫɢɬɟɥɶɧɨ ɭɫɤɨɪɟɧɢɹ ɧɚ ɊɈ, ɩɨɥɭɱɚɟɦ:

dȦPO		M iP MPO .		(2.44)
dt		JȾȼ iP2 JPO

Ɉɬɫɸɞɚ ɦɨɠɧɨ ɧɚɣɬɢ ɨɩɬɢɦɚɥɶɧɨɟ ɩɟɪɟɞɚɬɨɱɧɨɟ ɨɬɧɨɲɟɧɢɟ ɪɟɞɭɤɬɨɪɚ, ɨɛɟɫɩɟɱɢɜɚɸɳɟɟ ɦɚɤɫɢɦɚɥɶɧɨɟ ɡɧɚɱɟɧɢɟ ɭɫɤɨɪɟɧɢɹ dȦPO dt ,

iP.ɈɉɌ	ɆɊɈ		§	ɆɊɈ ·	2	J	(2.45)
			¨	¸		PO .
	Ɇ		©	Ɇ ¹		JȾȼ
Ɍɚɤ ɤɚɤ ɩɪɢ ɪɚɡɝɨɧɟ ɢ ɬɨɪɦɨɠɟɧɢɢ ɆɊɈ						ɪɚɡɥɢɱɧɵ, ɬɨ ɡɧɚɱɟɧɢɟ iɊ.ɈɉɌ ɩɨ
ɮɨɪɦɭɥɟ (2.45) ɨɞɧɨɡɧɚɱɧɨ ɨɩɪɟɞɟɥɹɟɬɫɹ ɥɢɲɶ ɞɥɹ ɆɊɈ							0, ɤɨɝɞɚ
	iP.ɈɉɌ			JPO .			(2.46)
				JȾȼ

ɇɟɨɛɯɨɞɢɦɨ ɩɨɞɱɟɪɤɧɭɬɶ ɭɫɥɨɜɧɨɫɬɶ ɬɟɪɦɢɧɚ «ɨɩɬɢɦɚɥɶɧɨɟ ɩɟɪɟɞɚɬɨɱɧɨɟ ɨɬɧɨɲɟɧɢɟ». ȼɟɥɢɱɢɧɚ iP.ɈɉɌ ɩɨɥɭɱɟɧɚ ɬɨɥɶɤɨ ɢɡ ɨɞɧɨɝɨ ɭɫɥɨɜɢɹ ɨɛɟɫɩɟɱɟɧɢɹ

ɧɚɢɛɨɥɶɲɟɝɨ ɭɫɤɨɪɟɧɢɹ ɪɚɛɨɱɟɝɨ ɨɪɝɚɧɚ ɩɪɢ ɡɚɞɚɧɧɨɦ ɞɜɢɝɚɬɟɥɟ. ȼ ɫɬɨɪɨɧɟ ɨɫɬɚɜɥɟɧɵ ɜɨɩɪɨɫɵ ɫɨɝɥɚɫɨɜɚɧɢɹ ɫɤɨɪɨɫɬɟɣ ɢ ɦɨɳɧɨɫɬɟɣ ɞɜɢɝɚɬɟɥɹ ɢ ɪɚɛɨɱɟɝɨ ɨɪɝɚɧɚ, ɛɟɡ ɪɟɲɟɧɢɹ ɤɨɬɨɪɵɯ ɡɚɬɪɭɞɧɢɬɟɥɶɧɨ ɩɪɚɜɢɥɶɧɨ ɜɵɛɪɚɬɶ ɧɟɨɛɯɨɞɢɦɨɟ ɩɟɪɟɞɚɬɨɱɧɨɟ ɱɢɫɥɨ ɪɟɞɭɤɬɨɪɚ.

	ɉɪɢɦɟɪ 2.2.	Ⱦɥɹ ɦɟɯɚɧɢɡɦɚ ɫ ɞɜɢɝɚɬɟɥɟɦ (Ɋɇ 9 ɤȼɬ,	Kɇ 910 ɦɢɧ 1,
U	100 B , I	100 A ) ɢ ɫɭɦɦɚɪɧɵɦ ɦɨɦɟɧɬɨɦ ɢɧɟɪɰɢɢ J	1 ɤɝ ɦ2 ɪɚɫɫɱɢ-
H	H

ɬɚɬɶ: ɞɢɧɚɦɢɱɟɫɤɢɣ ɦɨɦɟɧɬ ɆȾɂɇ , ɭɫɤɨɪɟɧɢɟ ɷɥɟɤɬɪɨɩɪɢɜɨɞɚ İ, ɤɨɧɟɱɧɨɟ ɡɧɚ-

ɱɟɧɢɟ ɫɤɨɪɨɫɬɢ ȦɄɈɇ, ɭɝɨɥ ɩɨɜɨɪɨɬɚ ɜɚɥɚ ɞɜɢɝɚɬɟɥɹ Į ɡɚ ɩɪɨɦɟɠɭɬɨɤ ɜɪɟɦɟ-

ɧɢǻti ti ɌȾ 0,5 , ɟɫɥɢ, Ɇɋ 0,5 , ȦɇȺɑ 0,2. Ɉɫɧɨɜɧɨɟ ɭɪɚɜɧɟɧɢɟ ɞɜɢɠɟɧɢɹ ɜ ɨ.ɟ.

							d	Ȧ		.
	Ɇ		Ɇ	ɋ	ɌȾ
							dt

26

Ɇɟɯɚɧɢɱɟɫɤɚɹ ɩɨɫɬɨɹɧɧɚɹ ɜɪɟɦɟɧɢ ɞɜɢɝɚɬɟɥɹ:

J ZOH

.

ɌȾ

MH

Ɂɧɚɱɟɧɢɹ ZOH ɢ MH ɪɚɫɫɱɢɬɚɟɦ ɩɪɢ kɎɇ

1 ȼ ɫ (ɪɚɫɱɟɬ ɩɨ ɤɚɬɚɥɨɠɧɵɦ

ɞɚɧɧɵɦ ɞɜɢɝɚɬɟɥɹ – ɫɦ. ɩɪɢɦɟɪ 3.1).

ɋɤɨɪɨɫɬɶ ɢɞɟɚɥɶɧɨɝɨ ɯɨɥɨɫɬɨɝɨ ɯɨɞɚ

ZɈɇ

UH

100

100 ɪɚɞ ɫ.

kɎɇ

1

ɇɨɦɢɧɚɥɶɧɵɣ ɷɥɟɤɬɪɨɦɚɝɧɢɬɧɵɣ ɦɨɦɟɧɬ

Ɇɇ

kɎɇ UH

1 100

100 ɇ ɦ.

Ɇɟɯɚɧɢɱɟɫɤɚɹ ɩɨɫɬɨɹɧɧɚɹ ɜɪɟɦɟɧɢ

J ZOH

1 100

1 ɫ .

Ɍ

Ⱦ

MH

100

Ⱦɢɧɚɦɢɱɟɫɤɢɣ ɦɨɦɟɧɬ

ɋ

1,5 0,5

1.

ɆȾɂɇ

Ɇ

Ɇ

ɍɫɤɨɪɟɧɢɟ ɷɥɟɤɬɪɨɩɪɢɜɨɞɚ (ɩɪɢ tȻ

ɌȾ )

H

d

Z

dt

d

Z

M

M

M

1.

dt

C

Ⱦɂɇ

ɌȾ

ɉɪɢɪɚɳɟɧɢɟ ɫɤɨɪɨɫɬɢ ɡɚ ɩɪɨɦɟɠɭɬɨɤ ɜɪɟɦɟɧɢ 'ti

ti

ɌȾ

0,5 :

ɋ

i

1,5 0,5 0,5

'Z

Ɇ

Ɇ

't

0,5 .

Ʉɨɧɟɱɧɨɟ ɡɧɚɱɟɧɢɟ ɫɤɨɪɨɫɬɢ ɧɚ ɭɱɚɫɬɤɟ

ɇȺɑ

0,2 0,5

Z

ɄɈɇ

Z

'Z

0,7 .

ɉɪɢɪɚɳɟɧɢɟ ɭɝɥɚ ɩɨɜɨɪɨɬɚ

ɇȺɑ

ɄɈɇ

't

0,7 0,2

0,5

'D

Z

Z

0,225 .

2

2

Ɉɩɪɟɞɟɥɢɦ ɩɨɥɭɱɟɧɧɵɟ ɡɧɚɱɟɧɢɹ ɜ ɚɛɫɨɥɸɬɧɵɯ ɟɞɢɧɢɰɚɯ:

ɆȾɂɇ			ɆȾɂɇ Ɇɇ			1 100	100 ɇ ɦ;
H		H ZɈɇ			1 100 100 ɪɚɞ ɫ2 ;
		tȻ			1
'Z		'Z ZɈɇ			0,5 100		50 ɪɚɞ ɫ ;
ZɄɈɇ		ZɇȺɑ ZɈɇ				0,7 100	70 ɪɚɞ ɫ ;
'D 'D	ZɈɇ tȻ				0,225 100 1 22,5 ɪɚɞ.

27

ȦɇȺɑ

2 1 ti .

ɌȾ

J 1ɤɝ ɦ2

ɉɪɢɦɟɪ 2.3. Ⱦɥɹ ɞɜɢɝɚɬɟɥɹ (Ȧ	0ɇ	100 ɪɚɞ ɫ, Ɇ 100 ɇ ɦ,			J	1ɤɝ ɦ2 )
		ɇ
				t , ɟɫɥɢ
ɪɚɫɫɱɢɬɚɬɶ ɭɫɤɨɪɟɧɢɟ ɢ ɩɨɫɬɪɨɢɬɶ ɩɟɪɟɯɨɞɧɵɣ ɩɪɨɰɟɫɫ							M 2,
			Ȧ

ȦɇȺɑ 0, Ɇɋ 0.

Ⱦɥɹ ɪɚɫɱɟɬɚ ɢ ɩɨɫɬɪɨɟɧɢɹ ɧɚɝɪɭɡɨɱɧɵɯ ɞɢɚɝɪɚɦɦ Ɇ(t) ɢ Ȧ(t) ɢɫɩɨɥɶɡɭɟɬɫɹ ɪɟɲɟɧɢɟ ɨɫɧɨɜɧɨɝɨ ɭɪɚɜɧɟɧɢɹ ɞɜɢɠɟɧɢɹ

			ɋ			d	Ȧ		,
Ɇ		Ɇ
				ɌȾ
						dt

ɢɡ ɤɨɬɨɪɨɝɨ ɞɥɹ ɤɨɧɟɱɧɵɯ ɩɪɢɪɚɳɟɧɢɣ ɩɪɢ Ɇ = const ɢ Ɇɋ = const ɞɥɹ ɡɚɞɚɧɧɨɝɨ ti ɩɨɥɭɱɢɦ ɩɪɢɪɚɳɟɧɢɟ ɫɤɨɪɨɫɬɢ

ǻȦ M MC ti .

Ɍɞ

ɢ ɡɧɚɱɟɧɢɟ ɫɤɨɪɨɫɬɢ ɜ ɤɨɧɰɟ ɭɱɚɫɬɤɚ

ȦȦɇȺɑ ǻȦ.

Ɇɟɯɚɧɢɱɟɫɤɚɹ ɩɨɫɬɨɹɧɧɚɹ ɜɪɟɦɟɧɢ

J Ȧ0H 1 100

1 c .

Ɍ

Ⱦ

MH

100

ɉɪɢɪɚɳɟɧɢɟ ɫɤɨɪɨɫɬɢ

C ti

2 0 ti ,

M

M

ǻȦ

ɌȾ

ɌȾ

ɢ ɩɪɢ ti = ɌȾ ɩɨɥɭɱɚɟɦ ǻȦ 2 .

ɋɤɨɪɨɫɬɶ ɡɚ ɷɬɨ ɜɪɟɦɹ ɞɨɫɬɢɝɧɟɬ ɡɧɚɱɟɧɢɹ

ȦM

2M(t)

Ȧ(t)

1

t

1

Ɋɢɫ. 2.10. Ɇɟɯɚɧɢɱɟɫɤɢɣ ɩɟɪɟɯɨɞɧɵɣ ɩɪɨɰɟɫɫ ɩɪɢ Ɇ=const

ɉɪɢɪɚɳɟɧɢɟ ɫɤɨɪɨɫɬɢ

ǻȦ M MC ti

ɌȾ

								0 2
	Ȧ		Ȧ	ɇȺɑ ǻȦ					2 .
Ɂɧɚɱɟɧɢɹ						1		ɫɤɨɪɨɫɬɶ	ɞɨɫɬɢɝ-
					Ȧ

ɧɟɬ ɡɚ ¨t = 0,5·ɌȾ, ɜ ɷɬɨɬ ɦɨɦɟɧɬ ɜɪɟɦɟɧɢ ɪɚɡɝɨɧ ɩɪɟɤɪɚɳɚɸɬ, ɫɧɢɠɚɹ ɦɨɦɟɧɬ ɞɜɢɝɚɬɟɥɹ ɞɨ ɜɟɥɢɱɢɧɵ ɫɬɚɬɢɱɟɫɤɨɝɨ ɦɨɦɟɧɬɚ Ɇ = Ɇɋ (ɫɦ. ɪɢɫ. 2.10).

ɉɪɢɦɟɪ 2.4.	Ⱦɥɹ	ɞɜɢɝɚɬɟɥɹ
(Ȧ0ɇ 100 ɪɚɞ ɫ,	Ɇɇ	100 ɇ ɦ,

ɌȾ=1 ɫ) ɪɚɫɫɱɢɬɚɬɶ ɭɫɤɨɪɟɧɢɟ ɢ ɩɨɫɬɪɨɢɬɶ ɩɟɪɟɯɨɞɧɵɣ ɩɪɨɰɟɫɫ ɪɟɜɟɪɫɚ Ȧ t , ɟɫɥɢ

1, Ɇɋ 1, M – 2.

28

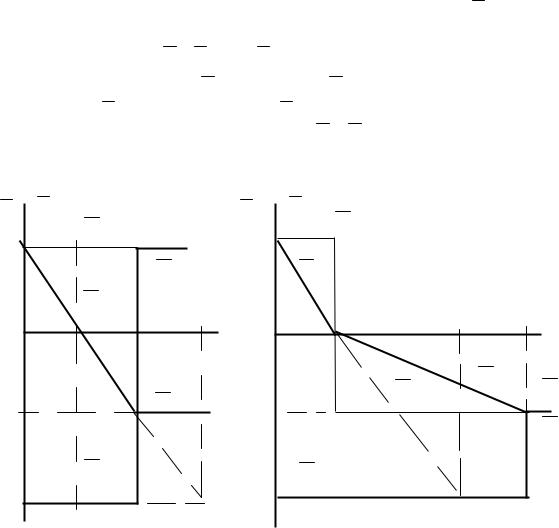
Ɂɚ ɛɚɡɨɜɨɟ ɜɪɟɦɹ tȻ = ɌȾ ɩɪɢɪɚɳɟɧɢɟ ɫɤɨɪɨɫɬɢ ɪɚɜɧɨ ǻȦ – 3, ɤɨɧɟɱɧɚɹ ɫɤɨɪɨɫɬɶ

Ȧ ȦɇȺɑ ǻȦ 1 3 – 2.

Ⱦɜɢɝɚɬɟɥɶ ɨɫɬɚɧɨɜɢɬɫɹ ( ȦɄɈɇ 0 ) ɩɪɢ ǻȦ – 1 ɡɚ ɜɪɟɦɹ ti = ɌȾ / 3. Ɋɟɜɟɪɫ ɡɚɤɨɧɱɢɬɫɹ ɩɪɢ ȦɄɈɇ – 1, ɩɪɢ ɷɬɨɦ ǻȦ – 2, ti = 2·ɌȾ / 3. ȼ ɷɬɨɬ ɦɨɦɟɧɬ ɜɪɟɦɟɧɢ ɫɥɟɞɭɟɬ ɫɧɢɡɢɬɶ ɦɨɦɟɧɬ ɞɜɢɝɚɬɟɥɹ ɞɨ M Ɇɋ. Ɋɚɫɫɦɨɬɪɟɧɧɵɣ ɩɟɪɟɯɨɞɧɵɣ ɩɪɨɰɟɫɫ ɫɩɪɚɜɟɞɥɢɜ ɞɥɹ ɚɤɬɢɜɧɨɝɨ ɫɬɚɬɢɱɟɫɤɨɝɨ ɦɨɦɟɧɬɚ (ɫɦ. ɪɢɫ. 2.11,ɚ).

Ȧ	M
	MC(t)
1
	M(t)
	Ȧ(t)
0	TȾ
	t
-1	Ȧ(t)
	M(t)
-2
	ɚ

Ȧ	M
	MC(t)
	1
	Ȧ(t)
	TȾ/3	TȾ
	0	t
		Ȧ(t)
	MC(t)	Ȧ(t)
	-1
		Ɇ(t)
	M(t)
	-2
	ɛ

Ɋɢɫ. 2.11. Ʉ ɩɪɢɦɟɪɭ 2.4: ɚ – ɩɪɢ ɚɤɬɢɜɧɨɦ ɆC;

ɛ – ɩɪɢ ɪɟɚɤɬɢɜɧɨɦ ɆC

ɉɪɢ ɪɟɚɤɬɢɜɧɨɦ ɫɬɚɬɢɱɟɫɤɨɦ ɦɨɦɟɧɬɟ, ɤɨɬɨɪɵɣ ɢɡɦɟɧɹɟɬ ɫɜɨɣ ɡɧɚɤ ɩɪɢ ɢɡɦɟɧɟɧɢɢ ɧɚɩɪɚɜɥɟɧɢɹ ɞɜɢɠɟɧɢɹ, ɩɟɪɟɯɨɞɧɵɣ ɩɪɨɰɟɫɫ ɪɚɫɩɚɞɚɟɬɫɹ ɧɚ ɞɜɚ ɷɬɚɩɚ. Ⱦɨ ɨɫɬɚɧɨɜɤɢ ɞɜɢɝɚɬɟɥɹ ɩɟɪɟɯɨɞɧɵɣ ɩɪɨɰɟɫɫ ɩɪɨɬɟɤɚɟɬ ɬɚɤɠɟ, ɤɚɤ ɢ

ɩɪɢ ɚɤɬɢɜɧɨɦ Ɇɋ. Ⱦɜɢɝɚɬɟɥɶ ɨɫɬɚɧɨɜɢɬɫɹ,

– 1, ɜɪɟɦɹ ɬɨɪ-

Ȧ

ɄɈɇ

0 , ɬɨɝɞɚ ǻȦ

ɦɨɠɟɧɢɹ

ti = ɌȾ / 3.

ɉɪɢ ɢɡɦɟɧɟɧɢɢ

ɧɚɩɪɚɜɥɟɧɢɹ

ɞɜɢɠɟɧɢɹ ɦɟɧɹɸɬɫɹ ɧɚɱɚɥɶɧɵɟ ɭɫɥɨɜɢɹ:

ɇȺɑ 0, Ɇɋ –1, M

– 2, ɧɚɱɚɥɶɧɨɟ ɜɪɟɦɹ ¨tɇȺɑ = ɌȾ / 3.

Ȧ

Ɍɨɝɞɚ ɩɪɢɪɚɳɟɧɢɟ ɫɤɨɪɨɫɬɢ ɫɨɫɬɚɜɢɬ

C ti

2 1 ti

M

M

- ti

.

ǻȦ

ɌȾ

ɌȾ

ɌȾ

ɉɪɢ ti = ɌȾ ɩɪɢɪɚɳɟɧɢɟ ɫɤɨɪɨɫɬɢ ǻȦ

– 1,

ȦɄɈɇ – 1, ɪɚɡɝɨɧ ɜ ɨɛɪɚɬɧɭɸ

ɫɬɨɪɨɧɭ ɩɪɨɢɡɨɣɞɟɬ ɡɚ ¨t = ɌȾ, ɪɟɜɟɪɫ ɡɚɤɨɧɱɢɬɫɹ ɡɚ ¨t = 4·ɌȾ / 3.

29

ȼ ɷɬɨɬ ɦɨɦɟɧɬ ɜɪɟɦɟɧɢ ɫɥɟɞɭɟɬ ɫɧɢɡɢɬɶ ɦɨɦɟɧɬ ɞɜɢɝɚɬɟɥɹ ɞɨ M Ɇɋ

(ɫɦ. ɪɢɫ. 2.11, ɛ). Ɍɚɤɢɦ ɨɛɪɚɡɨɦ, ɩɪɢ ɪɟɚɤɬɢɜɧɨɦ Ɇɋ ɜɪɟɦɹ ɪɟɜɟɪɫɚ ɭɜɟɥɢɱɢɥɨɫɶ ɜɞɜɨɟ.

ɉɪɢɦɟɪ 2.5. Ⱦɥɹ ɞɜɢɝɚɬɟɥɹ (Ȧ	0ɇ	100 ɪɚɞ ɫ, Ɇ 100 ɇ ɦ, J 1 ɤɝ ɦ2 )
		ɇ

ɩɨɫɬɪɨɢɬɶ ɩɟɪɟɯɨɞɧɵɣ ɩɪɨɰɟɫɫ Ȧ(t), ɟɫɥɢ ɦɨɦɟɧɬ ɞɜɢɝɚɬɟɥɹ ɢɡɦɟɧɹɟɬɫɹ ɩɨ ɡɚ-

ɤɨɧɭ M(t) = 0,5 + sin(t), ɚɤɬɢɜɧɵɣ ȦɇȺɑ 0, Ɇɋ 1.

Ɋɚɫɫɦɨɬɪɢɦ ɩɨɜɟɞɟɧɢɟ ɞɜɢɝɚɬɟɥɹ ɧɚ ɧɚɱɚɥɶɧɨɦ ɭɱɚɫɬɤɟ.

Ʉɨɝɞɚ ɦɨɦɟɧɬ ɞɜɢɝɚɬɟɥɹ ɦɟɧɶɲɟ ɫɬɚɬɢɱɟɫɤɨɝɨ ɚɤɬɢɜɧɨɝɨ ɦɨɦɟɧɬɚ Ɇ < MC, ɬɨ ɩɨɞ ɞɟɣɫɬɜɢɟɦ ɚɤɬɢɜɧɨɝɨ MC ɞɜɢɝɚɬɟɥɶ ɧɚɱɢɧɚɟɬ ɪɚɡɝɨɧɹɬɶɫɹ ɜ ɫɬɨɪɨɧɭ, ɩɪɨɬɢɜɨɩɨɥɨɠɧɭɸ ɡɧɚɤɭ ɦɨɦɟɧɬɚ ɞɜɢɝɚɬɟɥɹ, Ȧ < 0.

ɉɪɢ Ɇ = MC ɫɧɢɠɟɧɢɟ ɫɤɨɪɨɫɬɢ ɩɪɟɤɪɚɬɢɬɫɹ, ɚ ɩɪɢ Ɇ > MC ɫɤɨɪɨɫɬɶ ɧɚɱɧɟɬ

ɧɚɪɚɫɬɚɬɶ ɞɨ ɧɭɥɹ, ɢ ɬɨɥɶɤɨ ɩɨɫɥɟ ɩɟɪɟɯɨɞɚ ɱɟɪɟɡ ɧɭɥɶ ɧɚɱɧɟɬɫɹ ɪɚɡɝɨɧ ɞɜɢɝɚɬɟɥɹ ɜ ɡɚɞɚɧɧɨɦ ɧɚɩɪɚɜɥɟɧɢɢ.

ȿɫɥɢ ɦɨɦɟɧɬ ɞɜɢɝɚɬɟɥɹ ɹɜɥɹɟɬɫɹ ɮɭɧɤɰɢɟɣ ɜɪɟɦɟɧɢ, ɬɨ ɞɥɹ ɩɨɥɭɱɟɧɢɹ ɜɵɪɚɠɟɧɢɹ ɧɚɝɪɭɡɨɱɧɨɣ ɞɢɚɝɪɚɦɦɵ ɫɤɨɪɨɫɬɢ ɩɪɢɯɨɞɢɬɫɹ ɢɧɬɟɝɪɢɪɨɜɚɬɶ ɨɫɧɨɜɧɨɟ ɭɪɚɜɧɟɧɢɟ ɞɜɢɠɟɧɢɹ. Ɍɚɤ ɤɚɤ ɢɧɬɟɝɪɢɪɨɜɚɧɢɟ ɜɵɩɨɥɧɹɟɬɫɹ ɜ ɨ.ɟ., ɬɨ ɜɪɟɦɹ ɬɚɤɠɟ ɩɪɢɯɨɞɢɬɫɹ ɜɜɨɞɢɬɶ ɜ ɨ.ɟ., ɩɪɢ ɷɬɨɦ ɡɚ ɛɚɡɨɜɨɟ ɡɧɚɱɟɧɢɟ ɜɪɟɦɟɧɢ ɭɞɨɛɧɨ ɩɪɢɧɹɬɶ tȻ = ɌȾ. Ɍɨɝɞɚ ɜ ɮɭɧɤɰɢɹɯ sin(t) ɢ cos(t) ɩɨɥɚɝɚɟɦ, ɱɬɨ Ȧ = 1 ɪɚɞ/ɫ, ɢ t ɩɪɢɧɢɦɚɟɬ ɪɚɡɦɟɪɧɨɫɬɶ ɪɚɞɢɚɧɚ.

³t

C dt

³t 0,5 sin

C dt 0,5

C

1 cos

.

t

M

M

t

M

M

t

t

Ȧ

0

0

ɇɚ ɪɢɫ. 2.12 ɩɪɢɜɟɞɟɧ ɦɟɯɚɧɢɱɟɫɤɢɣ ɩɟɪɟɯɨɞɧɵɣ ɩɪɨɰɟɫɫ ɞɥɹ ɫɢɧɭɫɨɢɞɚɥɶɧɨɝɨ ɢɡɦɟɧɟɧɢɹ ɦɨɦɟɧɬɚ Ɇ(t). Ɂɧɚɱɟɧɢɟ t, ɩɪɢ ɤɨɬɨɪɨɦ M MC ɢ ɆȾɂɇ=0,

ɚ ɫɤɨɪɨɫɬɶ ɞɨɫɬɢɝɚɟɬ ɦɚɤɫɢɦɚɥɶɧɨɝɨ ɨɬɪɢɰɚɬɟɥɶɧɨɝɨ ɡɧɚɱɟɧɢɹ, ɧɚɣɞɟɦ ɢɡ ɮɨɪɦɭɥɵ

					0,5 sin t 1.
	Ɇ		Ɇɋ
Ɍɨɝɞɚ
t		arcsin 1 0,5 0,524;
ȦɆɂɇ 0,5 Ɇɋ t 1 cos t					0,5 1 0,524 1 cos 0,524 -0,128.

Ⱦɥɹ ɨɩɪɟɞɟɥɟɧɢɹ ɜɪɟɦɟɧɢ ɩɟɪɟɯɨɞɚ ɫɤɨɪɨɫɬɢ ɱɟɪɟɡ ɧɭɥɶ ɜɨɫɩɨɥɶɡɭɟɦɫɹ ɦɟɬɨɞɨɦ ɩɨɞɛɨɪɚ, ɬɚɤ ɤɚɤ ɭɪɚɜɧɟɧɢɟ Ȧ(t) – ɬɪɚɧɫɰɟɧɞɟɧɬɧɨɟ. Ɋɟɡɭɥɶɬɚɬɵ ɪɚɫɱɟɬɚ ɫɜɟɞɟɧɵ ɜ ɬɚɛɥ. 2.1.

												Ɍɚɛɥɢɰɚ 2.1
						Ɋɚɫɱɟɬ Ȧ(t) ɞɥɹ ɩɪɢɦɟɪɚ 2.5
	t,c				0	0,524	1	1,11	1,5		2		3
	M(t)				0,5	1	1,34	1,4	1,5		1,4		0,64
	cos(t)				1	0,866	0,54	0,444	0,07		–0,416		–0,99
	Ȧ( t )				0	–0,128	–0,04	0,000	0,16		0,416		0,49
	Ɍɚɤɢɦ ɨɛɪɚɡɨɦ,					ɫɤɨɪɨɫɬɶ ɩɟɪɟɯɨɞɢɬ ɱɟɪɟɡ ɧɭɥɶ ɩɪɢ t					1,11. ɉɪɢ tȻ = 1 ɫ
				t 1,11 c .
ɜɪɟɦɹ t

30