
- •Глава 1. Введение в математический анализ
- •§ 1. Множество r действительных чисел и его свойства
- •§ 2. Числовые множества, их границы
- •§ 3. Абсолютная величина числа
- •§ 4. Понятие числовой последовательности. Бесконечно большая и бесконечно малая последовательности, их свойства
- •§ 5. Сходящиеся последовательности, их свойства
- •§ 6. Монотонные последовательности. Число е
- •§ 7. Теорема Больцано-Вейерштрасса. Принцип сходимости
- •§ 8. Отображение множеств. Обратное отображение. Композиция отображений. Понятие действительной функции
- •§ 9. Арифметические операции над функциями. Композиция функций
- •§ 10. Ограниченные и неограниченные функции. Монотонные функции
- •§ 11. Четные и нечетные функции. Периодические функции
- •§ 12. Обратная функция
§ 11. Четные и нечетные функции. Периодические функции
Определение 1. Функция![]() называетсячетной (нечетной),
если вместе с каждым значением переменной
называетсячетной (нечетной),
если вместе с каждым значением переменной![]() значение –хтакже принадлежит
значение –хтакже принадлежит![]() и выполняется равенство
и выполняется равенство
![]() (11.1)
(11.1)
Таким образом, функция может быть четной
или нечетной только тогда, когда ее
область определения симметрична
относительно начала координат на
числовой прямой (числа х и –ходновременно принадлежат![]() ).
Например, функция
).
Например, функция![]() не является четной и нечетной, так как
ее область определения
не является четной и нечетной, так как
ее область определения![]() не симметрична относительно начала
координат.
не симметрична относительно начала
координат.
Функция
![]() четная, так как
четная, так как![]() симметрична относительно начала
координат и
симметрична относительно начала
координат и![]() .
.
Функция
![]() нечетная, так как
нечетная, так как![]() и
и![]()
![]() .
.
Функция
![]() не является четной и нечетной, так как
хотя
не является четной и нечетной, так как
хотя![]() и симметрична относительно начала
координат, равенства (11.1) не
выполняются. Например,
и симметрична относительно начала
координат, равенства (11.1) не
выполняются. Например,![]() .
.
График четной функции симметричен
относительно оси Оу, так как если
точка![]() принадлежит графику, то и точка
принадлежит графику, то и точка![]() тоже принадлежит графику. График нечетной
функции симметричен относительно начала
координат, так как если
тоже принадлежит графику. График нечетной
функции симметричен относительно начала
координат, так как если![]() принадлежит графику, то и точка
принадлежит графику, то и точка![]() тоже принадлежит графику.
тоже принадлежит графику.
При доказательстве четности или нечетности функции бывают полезны следующие утверждения.
Теорема 1. а) Сумма двух четных (нечетных) функций есть функция четная (нечетная).
б) Произведение двух четных (нечетных) функций есть функция четная.
в) Произведение четной и нечетной функций есть функция нечетная.
г) Если f– четная
функция на множествеХ, а функцияg определена на
множестве![]() ,
то функция
,
то функция![]() –
четная.
–
четная.
д) Если f– нечетная
функция на множествеХ, а функцияg определена на
множестве![]() и четная (нечетная), то функция
и четная (нечетная), то функция![]() –
четная (нечетная).
–
четная (нечетная).
Доказательство. Докажем, например, б) и г).
б) Пусть
![]() и
и![]() –
четные функции. Тогда
–
четные функции. Тогда![]() ,
поэтому
,
поэтому![]() .
Аналогично рассматривается случай
нечетных функций
.
Аналогично рассматривается случай
нечетных функций![]() и
и![]() .
.
г) Пусть f – четная
функция. Тогда![]() .
.
Остальные утверждения теоремы доказываются аналогично. Теорема доказана.
Теорема 2. Любую функцию![]() ,
заданную на множествеХ, симметричном
относительно начала координат, можно
представить в виде суммы четной и
нечетной функций.
,
заданную на множествеХ, симметричном
относительно начала координат, можно
представить в виде суммы четной и
нечетной функций.
Доказательство. Функцию![]() можно записать в виде
можно записать в виде
![]() .
.
Функция
![]() – четная, так как
– четная, так как![]() ,
а функция
,
а функция![]() – нечетная, поскольку
– нечетная, поскольку![]() .
Таким образом,
.
Таким образом,![]() ,
где
,
где![]() –
четная, а
–
четная, а![]() –
нечетная функции. Теорема доказана.
–
нечетная функции. Теорема доказана.
Определение 2. Функция![]() называетсяпериодической, если
существует число
называетсяпериодической, если
существует число![]() ,
такое, что при любом
,
такое, что при любом![]() числа
числа![]() и
и![]() также
принадлежат области определения
также
принадлежат области определения![]() и выполняются равенства
и выполняются равенства
![]() .
.
Такое число Tназываетсяпериодом функции![]() .
.
Из определения 1 следует, что если Т
– период функции![]() ,
то и число –Т тоже является
периодом функции
,
то и число –Т тоже является
периодом функции ![]() (так
как при заменеТ на –Т равенство
сохраняется). С помощью метода
математической индукции можно показать,
что еслиТ– период функцииf,
то и
(так
как при заменеТ на –Т равенство
сохраняется). С помощью метода
математической индукции можно показать,
что еслиТ– период функцииf,
то и![]() ,
тоже является периодом. Отсюда следует,
что если функция имеет период, то она
имеет бесконечно много периодов.
,
тоже является периодом. Отсюда следует,
что если функция имеет период, то она
имеет бесконечно много периодов.
Определение 3. Наименьший из положительных периодов функции называется ееосновным периодом.
Теорема 3. ЕслиТ– основной период функцииf, то остальные периоды кратны ему.
Доказательство. Предположим
противное, то есть что существует период![]() функцииf (
функцииf (![]() >0),
не кратныйТ. Тогда, разделив
>0),
не кратныйТ. Тогда, разделив![]() наТ с остатком, получим
наТ с остатком, получим![]() ,
где
,
где![]() .
Поэтому
.
Поэтому
![]() ,
,
то есть
![]() – период функцииf,
причем
– период функцииf,
причем![]() ,
а это противоречит тому, чтоТ–
основной период функцииf.
Из полученного противоречия следует
утверждение теоремы. Теорема доказана.
,
а это противоречит тому, чтоТ–
основной период функцииf.
Из полученного противоречия следует
утверждение теоремы. Теорема доказана.
Хорошо известно, что тригонометрические
функции являются периодическими.
Основной период
![]() и
и![]() равен
равен![]() ,
,![]() и
и![]() .
Найдем период функции
.
Найдем период функции![]() .
Пусть
.
Пусть![]() - период этой функции. Тогда
- период этой функции. Тогда
![]() (так как
(так как![]() .
.
Отсюда

![]() или
или![]() или
или![]() или
или![]() .
.
Значение T, определяемое
из первого равенства, не может быть
периодом, так как зависит отх, т.е.
является функцией отх, а не постоянным
числом. Период определяется из второго
равенства:![]() .
Периодов бесконечно много, при
.
Периодов бесконечно много, при![]() наименьший
положительный период получается при
наименьший
положительный период получается при![]() :
:![]() .
Это – основной период функции
.
Это – основной период функции![]() .
.
Примером более сложной периодической функции является функция Дирихле
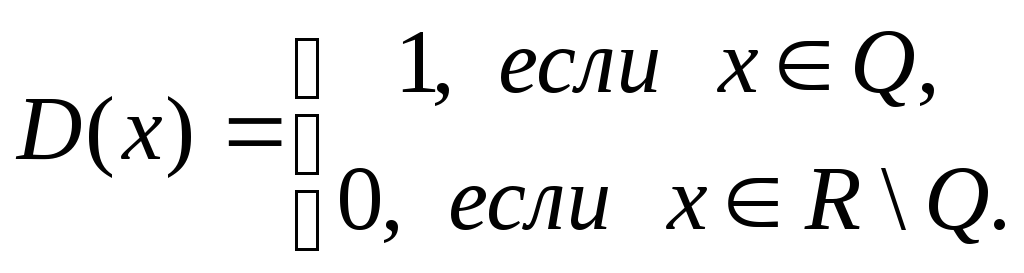
Заметим, что если T–
рациональное число, то![]() и
и![]() являются рациональными числами при
рациональномхи иррациональными
при иррациональномх. Поэтому
являются рациональными числами при
рациональномхи иррациональными
при иррациональномх. Поэтому

при любом рациональном числе T.
Следовательно, любое рациональное числоTявляется периодом
функции Дирихле. Ясно, что основного
периода у этой функции нет, так как есть
положительные рациональные числа, сколь
угодно близкие к нулю (например,
рациональное число![]() можно сделать выборомnсколь угодно близким к нулю).
можно сделать выборомnсколь угодно близким к нулю).
Теорема 4. Если функцияf
задана на множествеХи имеет
периодТ, а функцияg
задана на множестве![]() ,
то сложная функция
,
то сложная функция![]() тоже имеет периодТ.
тоже имеет периодТ.
Доказательство. Имеем![]() ,
поэтому
,
поэтому
![]() ,
,
то есть утверждение теоремы доказано.
Например, так как cos
x имеет период![]() ,
то и функции
,
то и функции![]() имеют период
имеют период![]() .
.
Определение 4. Функции, не являющиеся периодическими, называютсянепериодическими.
