Белозеров В.И. Учебное пособие по курсу Техническая термодинамика (исправлено)

ñèñò ñèñò

Химическим потенциалом M вещества называется удельный изо- барно-изотермический потенциал

M h TS, Äæ .

êã

9.3. Условия устойчивости и равновесия в

изолированной однородной системе

Термодинамический анализ позволяет показать, что из соображений термодинамической устойчивости системы для любого вещества должны выполняться условия

C > 0,	(9.3.1)
v

§ wP ·

¨ ¸ 0, (9.3.2)

© wV ¹T

т.е., во-первых, изохорная теплоемкость C всегда положительна и,

v

во-вторых, в изотермическом процессе увеличение давления всегда приводит к уменьшению объема вещества. Условие (9.3.1) называется условием термической устойчивости, а условие (9.3.2) – условием механической устойчивости.

Условия (9.3.1) и (9.3.2) можно объяснить так называемым принципом смещения равновесия (принцип Ле Шателье–Брауна), смысл которого заключается в том, что если система, находившаяся в равновесии, выводится из него, соответствующие параметры системы изменяются таким образом, чтобы система вернулась в состояние равновесия.

Рассмотрим условие равновесия в изолированной термодинамической системе.

Мысленно разделим эту систему на две подсистемы 1 и 2 и выясним, при каких условиях существует равновесие между этими подсистемами (рис. 9.3.1).

Поскольку система изолированная, то

V= const и U = const. Можно пред-

ставить себе такой бесконечно малый про-

Ðèñ. 9.3.1

121

цесс внутри изолированной системы, при котором либо меняется объем каждой из подсистем, либо меняется внутренняя энергия подсистем, либо то и другое вместе (при этом количество вещества в каждой из подсистем остается неизменным). Пусть для первой под-

системы объем меняется на величину dV , а внутренняя энергия –

1

на величину dU и для второй подсистемы – соответственно на dV

1 2

и dU . Объем и внутренняя энергия всей системы сохраняют посто-

2

янное значение, поэтому

dV1 dV2 è dU1 dU2 .

Ранее мы установили, что в изолированной системе в состоянии термодинамического равновесия энтропия системы сохраняет постоянное (максимальное) значение, т.е.

dS

0.

(9.3.3)

ñèñò

Энтропия является аддитивной величиной и

Sñèñò

S1 S2 ,

а в соответствии с (9.3.3)

dSñèñò

dS1 dS2

0.

(9.3.4)

Из уравнения TdS = dU + PdV следует, что

dS

1

dU

P

dV.

(9.3.5)

T

T

Таким образом, для подсистемы 1

dS

1

dU

1

P1

dV ,

1

T1

T1

1

для подсистемы 2

dS

1

dU

P2

dV .

2

2

T2

T2

2

В соответствии с уравнением (9.3.4) получаем

1

dU

P1

dV

1

dU

P2

dV

0

(9.3.6)

T

T

T

1

1

T

2

2

1

1

2

2

èëè

122

§	1		1		·	§	P		P	·
¨					¸dU1	¨	1		2	¸dV1 0.	(9.3.7)
									T2
©T1			T2 ¹			©T1				¹

Дифференциалы dU и dV независимы, т.е. может меняться внут-

11

ренняя энергия системы, а объем остается постоянным и наоборот, тогда

	1		1		0 è	P1		P2	0,
T1 T2						T1		T2
ò.å.
			T = T , P = P .
1					2	1	2

Итак, мы пришли к выводу, что температуры и давления в изолированной системе в состоянии равновесия одинаковы во всех частях системы.

9.4. Условия фазового равновесия

Рассмотрим изолированные системы, состоящие из двух (или более) фаз. Найдем общие условия фазового равновесия. Отличие от предыдущего случая (две подсистемы) состоит в том, что веще-

ство теперь находится в различных фазах.
Рассматривается система, для которой V	= const, G = const,
ñèñò	ñèñò

U= const (G – полное количество вещества в системе).

ñèñò

ñèñò

Пример. Одна часть сосуда постоянного объема с идеально теплоизолированными стенками заполнена водой, а другая – водяным паром, следовательно,

V = V +V ; G = G +G ; U = U +U ,

ñèñò	1 2	ñèñò		1 2	ñèñò	1	2
где индексами 1 и 2 обозначены фазы, отсюда
dV = – dV , dG = – dG , dU = – dU .							(à)
1	2	1		2	1	2
Поскольку
	dSñèñò	0	è	Sñèñò	S1 S2 ,		(*)
òî
	dSñèñò		dS1	dS2	0.

Для первой фазы S = f (V , U , G ) и в соответствии с этим

1 1 1 1

123

§ wS1

·

§ wS1 ·

§ wS1

·

dG1.

dS1

¨

¸

dU1 ¨

¸

dV1

¨

¸

(9.4.1)

© wU1 ¹V1 ,G1

© wV1 ¹U1 ,G1

© wG1 ¹U1 ,V1

Åñëè

§ wS

·

1

§ wS

·

P

§ wS

·

M

¨

1

¸

; ¨

1

¸

1

; ¨

1

¸

1

,

© wU1 ¹V1 ,G1

T1

© wV1 ¹U1 ,G1

T1

© wG1 ¹U1 ,V1

T1

то в соответствии с этим

dS

1

dU

1

P1

dV

M1

dG .

(9.4.2)

1

T1

T1

1

T1

1

Аналогично для второй фазы:

dS

2

1

dU

2

P2

dV

M2

dG .

(9.4.3)

T2

T2

2

T2

2

Подставляя (9.4.2), (9.4.3) в (*) и учитывая (а), получим

§ 1

1 ·

§ P

P

·

§ M

M

·

¨

¸dU1

¨

1

2

¸dV1 ¨

1

2

¸dG1

0.

(9.4.4)

©T1

T2 ¹

©T1

T2 ¹

©

T1

T2 ¹

Поскольку дифференциалы dU, dV, dG взаимно независимы, то

1

1

0,

P1

P2

0,

M1

M2

0

(9.4.5)

T1

T2

T1

T2

T1

T2

èëè

T

T

; P

P

; M

M

.

(9.4.6)

1

2

1

2

1

2

Таким образом, если две (и более) фазы находятся в равновесии, то температуры, давления и химические потенциалы этих фаз равны между собой.

124

9.5. Фазовые переходы

Фазовым переходом называется переход вещества из одной фазы в другую, сосуществующую с первой. Говоря о фазах чистого вещества, обычно имеют в виду агрегатные состояния вещества и поэтому говорят о газовой, жидкой и твердой фазах. Однако понятие фазы несколько уже понятия агрегатного состояния: некоторые вещества (например, лед) в твердом состоянии имеют несколько фаз. Тем не менее, мы в дальнейшем будем подразумевать под фазовым переходом переход вещества из одного агрегатного состояния в другое.

Фазовый переход из твердой фазы в газообразную, происходящий при очень низких давлениях, называется сублимацией. Из сказанного очевидно, что теплота сублимации должна быть больше, чем теплота плавления или теплота парообразования. При фазовом переходе резко изменяется плотность вещества, в случаях парообразования и сублимации плотность газовой фазы всегда меньше, чем плотность жидкой или твердой фаз.

Принята следующая классификация точек фазового перехода: точка перехода «жидкость–пар» называется точкой кипения (она же точка конденсации), точка перехода «твердое тело–жидкость» называется точкой плавления (она же точка затвердевания), а точка перехода «твердое тело–пар» называется точкой сублимации.

С повышением температуры в веществе происходит некоторое дробление молекулярных ассоциаций (в твердой фазе – разрыхление кристаллов). Этот процесс заметно ускоряется вблизи точек перехода, в которых изменение молекулярной структуры происходит скач- кообразно.

Твердые вещества могут образовывать не одну, а несколько кристаллических модификаций (например, лед), каждая из которых существует при определенных параметрах состояния.

При анализе фазовых равновесий и процессов фазовых переходов важную роль играет так называемое правило фаз Гиббса. Оно устанавливает зависимость между числом независимых переменных, определяющих состояние термодинамической системы, находящейся в равновесии (эти независимые переменные часто называют степенями свободы системы), числом фаз и числом компонентов системы.

125

Правило фаз формулируется следующим образом:

n r 2 ,

(9.5.1)

где – число степеней свободы термодинамической системы; n –

число компонентов системы; r – число фаз в системе.

Правило фаз, справедливое для систем с любым количеством компонентов, играет особенно важную роль в химической термодинамике.

Для чистых веществ (однокомпонентная система, n = 1)

3 r.

(9.5.2)

Для чистых веществ в однофазной системе (r = 1) число степеней свободы = 2. Это означает, что если для такой системы произвольно задать, например, P и T, то все остальные параметры системы будут определены однозначно.

Для двухфазной системы, находящейся в равновесии, r = 2, = 1, т.е. любой параметр определяет равновесное состояние каждой фазы системы, например, давление P или температура T.

Линию фазового перехода можно изобразить на PT-диаграмме, если нанести состояния, соответствующие давлениям и температурам фазового перехода.

Для трехфазной системы r = 3 и число степеней свободы = 0. Это означает, что в однокомпонентной системе три фазы могут находиться в равновесии лишь при вполне определенных температурах T и давлении P, характерных для данного конкретного вещества.

Hа рис. 9.5.1 изображена PT-диаграмма вещества с нанесенными на ней кривыми фазовых переходов.

P				A	K
				Жидкая
Твердая фаза			C	ôàçà
	Плавление			D		P = const
(затвердевание)				Кипение
				(конденсация)
		O
		ривая
		àöèè
	сублим			Газообразная
	Ê
B				ôàçà
						T

Ðèñ. 9.5.1

Слева от линии АОВ

расположена область твердого состояния вещества, справа от линии

КОВ – область газообразного состояния вещества, а между линиями АО и КО – область жидкого состояния. Кривая кипения обычно называется кривой (или линией) насыщения. Точка О представля-

126

ет собой тройную точку, в которой вещество сосуществует в трех агрегатных состояниях. Для воды тройная точка соответствует температуре 0,01°С и давлению 610,8 Па. Кривая сублимации ОВ продолжается вниз в сторону низких температур. Кривая плавления ОА

уходит вверх, в сторону больших давлений, она не оканчивается даже при сверхвысоких давлениях (порядка десятка и сотен тысяч атмосфер). Линия насыщения ОК оканчивается в точке К, называемой критической точкой.

Линия сублимации и линия насыщения, как видно из рис. 9.5.1, имеют положительный наклон. Это означает, что с ростом давления температура фазового перехода (сублимация и кипение) повышается. Линия плавления для различных веществ может иметь как положительный, так и отрицательный наклон.

9.6. Уравнение Клапейрона–Клаузиуса

Рассмотрим две фазы (1 и 2), находящиеся в равновесии при давлении P и температуре T; условие равновесия

M	P,T	M	2	P,T .
1

Изменим температуру в каждой из фаз на величину dT, а давление – на величину dP. Если фазы и при новых условиях остаются в равновесии, то и потенциалы фаз будут равны:

M1 P dP,T dT M2 P dP,T dT .

(9.6.1)

Очевидно, что функция M(P+dP, T+dT) может быть разложена в ряд Маклорена (используем только первое слагаемое разложения):

	§ wM ·			§ wM ·
M P dP,T dT	M P,T ¨		¸	dP ¨		¸	dT; (9.6.2)
	© wP ¹T			© wT ¹P

§ wM ·

ò.ê. ¨ ¸ © wP ¹T

§ wM ·

v è ¨ ¸ S, то ряд (9.6.2) может быть записан

© wT ¹P

следующим образом:
M P dP,T dT M P,T vdP SdT.	(9.6.3)

Подставляя это выражение в левую и правую части уравнения (9.6.1), получаем

127

Μ1 P,T v1dP S1dT Μ2 P,T v2dP S2dT. (9.6.4)

Учитывая, что Μ (P, T) = Μ (P, T), уравнение кривой фазового пе-

12

рехода (уравнение Клапейрона–Клаузиуса) принимает вид

dP		S2	S1	.	(9.6.5)
dT		v2	v1

Это уравнение однозначно связывает наклон линии фазового перехода на PT-диаграмме с величинами разности энтропий сосуще-

ствующих фаз (S и S ) и разности удельных объемов этих фаз (v и v ).

2 1 2 1

Уравнение второго закона термодинамики для обратимых процессов

TdS dh vdP

применительно к данному случаю (для P=const), следующее:

TdS dh.

Интегрируя это соотношение между точками 1 и 2, получаем

T S2 S1 h2 h1 .

(9.6.6)

Применительно к процессу фазового перехода разность энтальпий сосуществующих фаз представляет собой теплоту фазового перехода, т.е. количество тепла, которое поглощается (или выделяет-

ся) 1 кг вещества в процессе фазового перехода.
Обозначая теплоту фазового перехода через r = h			– h , получа-
	2		1
åì èç (9.6.6)
S2 S1	r
		.
	T

Подставляя это значение в уравнение (9.6.5), получаем уравне-

ние Клапейрона-Клаузиуса в следующем виде:

dP		r			.
						(9.6.7)
dT		T v	v
	2		1

Фазовый переход «жидкость – пар»

Применительно к фазовому переходу «жидкость – пар» уравнение (9.6.7) можно записать таким образом:

128

dPS		r	,	(9.6.8)
dT		T vcc vc

где r – теплота парообразования; vs – удельный объем пара на линии насыщения; vc– удельный объем жидкости на линии насыщения;

P – равновесное давление в точках фазового перехода «жидкость –

S

ïàð».

Поскольку vcc > vc, то из уравнения (9.6.8) следует, что dPS >0, ò.å. dT

с ростом температуры давление насыщения увеличивается.

Если давление пара мало, то vs >> vc и поэтому (vs – vc) можно заменить величиной vs. Кроме того, если давление пара мало, то этот пар можно рассматривать как идеальный газ, т.е.

vcc RT .

PS

Подставляя это выражение в уравнение (9.6.8) и выполняя несложные преобразования, получаем

	d ln PS				r	,
	dT				RT 2
откуда
ln PS ³		r			dT const.		(9.6.9)
		RT		2

При низких давлениях величина теплоты парообразования практически не зависит от температуры, тогда в уравнении (9.6.9) r можно вынести за интеграл:

ln P

r

const.

(9.6.10)

S	RT

Обычно константу интегрирования определяют по величине тем-

пературы нормального кипения T	(ïðè P = 760 ìì ðò. ñò.). Èç óðàâ-
H.Ê	S
нения (9.6.10)

	PS		r §		1		1 ·
ln				¨				¸,	(9.6.11)
	P		R		T		T
				©				¹
ôèç.àòì					í.ê

129

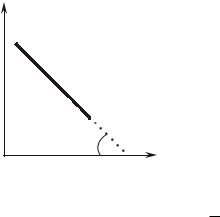
lnP

S

tg = r/R

1/T

Ðèñ. 9.6.1

§ 1 ·

т.е. при невысоких давлениях зависимость ln PS f ¨ ¸ должна

©T ¹

иметь линейный характер.

Как показывает обработка экспериментальных данных зависимости P – T для большого числа веществ, линейная зависимость

SS

1

ln P îò		действительно имеет место (рис. 9.6.1).

ST

Фазовый переход «твердое тело – жидкость»

Применительно к фазовому переходу «твердое тело–жидкость» (плавление) уравнение (9.6.7) можно записать в виде

	dP					Ο		,	(9.6.12)
	dT T				v	v
					æ	òâ

где O – теплота плавления; v – удельный объем жидкости на линии

æ

плавления; v – удельный объем твердой фазы на линии плавления.

òâ

Удельные объемы v и v обычно близки между собой; при этом

æòâ

возможны два случая: v > v и v < v . Из уравнения (9.6.12) оче-

	æ	òâ	æ	òâ
	видно, что в первом случае	dP	>0, т. е. с ростом давления темпера-
		dT
					dP
	тура плавления увеличивается; во втором случае величина
						<0,
					dT

т.е. с ростом давления температура плавления уменьшается (например, у воды).

130