lektsia_2_kurs_ITF

Теорема (Дирихле). Если функция f (x) удовлетворяет условиям Дирихле на отрезке ; , то ряд Фурье этой функции сходится на всем отрезке ; и сумма этого ряда равна f (x) в точках непрерывности функции,

f (x0 0) f (x0 0)

2

в точке x0 разрыва функции, и

f ( 0) f ( 0)

2

на концах отрезка ; .
Пример.	Разложить функцию	f (x) x в ряд Фурье и построить ее
график.
Решение.	Функция f (x) x	удовлетворяет условиям теоремы

Дирихле, и следовательно, может быть разложена в ряд Фурье. По формулам

(7) имеем:

1

a0

xdx ... 0,

1

an

xcosnxdx ... 0,

1

( 1)n 1 2

bn

xsinnxdx ...

.

n

Следовательно, согласно теореме Дирихле при x ;

sin2x

sin3x

sin4x

... ( 1)n 1

sinnx

x 2 sinx

2

3

4

n

... .

В точках x

и x сумма ряда Фурье по теореме Дирихле не совпадает

со значениями функции

f (x) x, а равна

f ( 0) f ( 0)

0 0

0.

2

2

График будет иметь вид:

21

	РЯДЫ ПО КОСИНУСАМ И СИНУСАМ
Если	f (x) - четная функция на отрезке ; , т.е. если							f ( x) f (x),
x ; ,	то ее коэффициенты Фурье bn 0, а коэффициенты a0 и an
вычисляются по формулам
			2
	a0					f (x)dx,
					0
		2					n 1,2,....
	an					f (x)cosnxdx,
					0
Аналогично, если f (x) - нечетная функция, то
						a0 0,
						an 0,
		2					n 1,2,....
	bn					f (x)sinnxdx,

Таким образом, если функция четная, то ее ряд Фурье содержит только косинусы, а если нечетная – только синусы.

Пример. Исследовать и разложить в ряд Фурье функцию f (x) x2. Решение. Эта функция удовлетворяет условиям Дирихле и,

следовательно, может быть разложена в ряд Фурье. Так как она четная, то bn 0.

		2		2	2
	a0		x2dx ...		,
				3
			0

22

		2		n
	an		x2 cosnxdx ...	( 1)2	4 .
			0	n

Тогда

	2		2					( 1)n						2						cos2x						cos3x
x				4						cosnx					4 cosx
			3					n2					3								2					3
						n 1
						2					cos2x					cos3x		cos4x
					3		4 cosx					2				3			4				... .
В точках x и x имеем:
					f ( 0) f ( 0)											0 2 0 2									2 .
																		2
									2

Следовательно, график имеет вид:

...

РЯД ФУРЬЕ С ПРОИЗВОЛЬНЫМ ПРОМЕЖУТКОМ

Если надо разложить в тригонометрический ряд функцию f (x) периода 2l , которая на отрезке l;l удовлетворяет условиям Дирихле, получим в интервале l;l

f (x) a0							bn sin n x ,
		an cosn x						(8)
	2	n 1				l	l
где
1 l			n x				(n 0,1,2,...),
an l	f	(x)cos		l	dx,			(9)
	l
	1 l			n x			(n 1,2,...),
bn l		f (x)sin		l		dx,		(10)
	l

23

ДВОЙНЫЕ ИНТЕГРАЛЫ ЗАДАЧИ, ПРИВОДЯЩИЕ К ПОНЯТИЮ ДВОЙНОГО ИНТЕГРАЛА

1. Задача о массе неопределенной пластины. Пусть плоская область G

заполнена веществом с известной плотностью (M) (x;y). Нужно найти массу (количество вещества) всей материальной области – «пластины». Под

плотностью	вещества в точке		M понимается предел средней плотности
бесконечно	малой	части G	содержащей точку M . Разобьем область
Gпроизвольным образом на n			частных областей 1, 2,..., n без общих
внутренних	точек,	площади	которых обозначим соответственно через

1, 2,..., n .

Предположим, что в пределах каждой частичной области плотность

постоянна и равна (Nk ) для k ,	где Nk k ; k - произвольная	точка
частичной области k . Тогда масса k	приближенна равна
mk ( k ; k ) k .
Для массы всей пластины получим приближенное выражение:
m n mk n ( k ; k ) k .		(1)
k 1	k 1

Пусть - наибольший из диаметров частичных областей. Диаметром области называется наибольшее из расстояний между точками ее границы. Например, диаметр прямоугольника равен его диагонали, диаметр эллипса – его большой оси. Для круга это определение диаметра совпадает с обычным. Сумма (1) будет тем точнее выражать искомую массу m, чем меньше будет каждый из диаметров частичных областей 1, 2,..., n . Поэтому за массу m естественно можно принять

24

m lim n ( k ; k ) k .

0 k 1

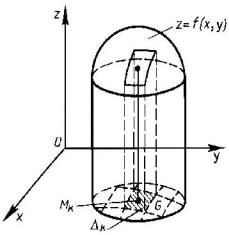
2. Задача об объеме цилиндроида. Пусть дана функция f (x;y),

непрерывная и неотрицательная в области G. Нужно найти объем тела, ограниченного сверху поверхностью z f (x;y), снизу областью G и с боком прямой цилиндрической поверхностью, направляющей которой служит замкнутый контур, ограничивающий область G. Такое тело для краткости будем называть цилиндроидом. В частности, когда верхнее основание цилиндроида есть плоскость, параллельная нижнему основанию, то цилиндроид называется цилиндром. Примером цилиндра служит круговой цилиндр.

Для нахождения объема V данного цилиндроида разобьем область G произвольным образом на n частичных областей 1, 2,..., n без общих внутренних точек, площади которых обозначим соответственно через1, 2,..., n . В каждой из этих частичных областей 1, 2,..., n выберем произвольную точку Nk k ; k и построим прямой цилиндрический столбик с основанием k и высотой f k ; k . Объем такого столбика равен f k ; k k . Сумма объемов этих цилиндрических столбиков представляет собой объем ступенчатого тела, приближенно занимающего объем данного цилиндроида. Следовательно

V n f ( k ; k ) k .

k 1

25

Эта сумма будет тем точнее выражать искомый объем V , чем меньше будет каждый из диаметров частичных областей 1, 2,..., n . Поэтому за объем V естественно принять

V lim n f ( k ; k ) k ,

0 k 1

где - наименьший из диаметров частичных областей 1, 2,..., n .

ОПРЕДЕЛЕНИЕ ДВОЙНОГО ИНЕТЕГРАЛА

Из решения приведенных выше задач видим, что, хотя эти задачи имеют различный смысл, математический аппарат для их решения один и тот же. Во всех этих задачах получаем выражение одного и того же вида

lim n f ( k ; k ) k ,	(2)
0 k 1
где f (x;y) - заданная в области G функция.
Определение. Если существует предел (2) не зависящий от способа
разбиения области G на частичные области k и выбора точек	Nk k ; k в

них, то он называется двойным интегралом от функции f (x;y) по области G и обозначается символом

f (x;y)d lim n		f ( k ; k ) k .	(3)
G	0 k 1

Функция f (x;y) в этом случае называется интегрируемой в области G. При этом f (x;y) называется подынтегральной функцией, d - элементов площади, G - областью интегрирования, x, y - переменными интегрирования, сумма

n f ( k ; k ) k - интегральной суммой.

k 1

Для двойного интеграла используется также обозначение

f (x;y)dxdy.

G

26

Определение. Кривая называется гладкой, если в каждой ее точке существует касательная и при переходе от точки к точке положение этой касательной меняется непрерывно.

Определение. Непрерывная кривая, составленная из конечного числа гладких кусков, называется кусочно-гладкой.

Теорема (существования двойного интеграла). Если область G с

кусочно-гладкой границей ограничена и замкнута, а функция f (x;y) непрерывна в области G, то эта функция интегрируема в области G.

Из рассматриваемых выше задач и определения двойного интеграла следует, что:

1.Двойной интеграл (3) с положительной подынтегральной функцией может быть истолкован физически, например как масса соответствующей пластины;

2.Тот же интеграл с неотрицательной подынтегральной функцией может быть истолкован геометрически как объем соответствующего цилиндроида. В частности, двойной интеграл от единичной функции

f (x;y) 1 по области G, т.е. интеграл d численно равен площади

G

области интегрирования:

SG d .

G

СВОЙСТВА ДВОЙНОГО ИНЕТГРАЛА

1. Постоянный множитель можно выносить за знак двойного интеграла, т.е.

kf (x;y)d k f (x;y)d .

GG

2.Двойной интеграл от суммы двух функций равен сумме двойных

интегралов от этих функций, т.е.

f1(x;y) f2(x;y) d f1(x;y)d f2(x;y)d .

G G G

27

Примечание. Свойство 2 распространяется на случай алгебраической

суммы любого конечного числа функций.
3.	Пусть область G разбита на две области G1 и G2 . Тогда
	f (x;y)d f (x;y)d f (x;y)d .
	G	G1			G2
4.	Если функция	f (x;y) 0	f (x;y) 0 в области G, то
	f (x;y)d
			0		f (x;y)d 0 .
	G			G

5. (Теорема о среднем). Двойной интеграл равен произведению значения подынтегральной функции в некоторой точке области интегрирования на площадь этой области.

ВЫЧИСЛЕНИЕ ДВОЙНЫХ ИНТЕГРАЛОВ

Пусть требуется вычислить двойной интеграл

f (x;y)d

G

от непрерывной в области G функции f (x;y).

1. Случай прямоугольной области.		Пусть область G -		прямоугольник
a x b,	c y d (кратко [a,b;c,d]). Тогда для двойного интеграла будем
иметь
		b d
				(4)
	f (x;y)d f (x;y)dy dx.
	G	a c
Обычно формулу (4) записывают в виде
		b	d
	f (x;y)d dx f (x;y)dy.			(5)
	G	a	c

Выражение, стоящее в правой части последней формулы, называется повторным интегралом. Для его вычисления надо последовательно взять два обычных интеграла: сначала внутренний интеграл

28

d

f (x;y)dy ,

c

в котором переменная x считается постоянной, а затем полученное выражение (оно зависит только от x) проинтегрировать по x от a до b - внешний интеграл.

Аналогично при втором способе перехода от двойной интегральной суммы к повторной получили бы

					d			b
		f (x;y)d dy f (x;y)dx.												(6)
		G			c			a
Пример. Вычислить двойной интеграл											I x2	y2 d , где область
											G
G - квадрат 0 x 1, 0 y 1.
Решение. По формуле (5) имеем:
1	1	2 2	1	2			y3			1	1 2		1
I dx (x y											dx x			dx
			)dy x y										3
0	0		0				3			0	0

13(x3 1)10 13 2 23.

Этот же двойной интеграл можно вычислить и по формуле (6).

2. Случай произвольной области. Пусть теперь G - область на плоскости xOy, изображенная на рисунке.

Тогда формулу (5) можно записать в виде:

29

	b	2(x)
f (x;y)d dx			f (x;y)dy,	(7)
G	a	1(x)
где y 1(x) и y 2(x) -	уравнения	нижней и верхней части контура
области G, на которые он делится точками A и B.
Можно интегрировать и в другом порядке – сначала по x, а затем по
y . Тогда получается формула
	d		2(y)
f (x;y)d dy			f (x;y)dx,	(8)
G	c	1(y)

где x 1(y) и x 2(y) - уравнения левой и правой частей контура области G, на которые он делится точками C и D .

Формулы (7) и (8) получены при условии, что область G пересекается прямыми, параллельными оси Oy (Ox), не более чем в двух точках. Если это условие нарушено, то область G разбивают на части.

Пример. Вычислить (x y)dxdy, по области G, ограниченной

G

линиями y x и y x2.

Решение. Нарисуем эту область:

Интегрируя сначалапо y , а потом по x, получаем

						1		x						1	xy y2							2 xx
(x y)dxdy= dx (x y)dy																										2 dx
G						0		x2						0
1			x	2				x	4			x	3			x	4			x	5			1			3
	2				x	3																						.
x			2					2		dx		2			4				10								20
0																								0

30