lektsia_2_kurs_ITF

x		Myz		, y	Mxz	, z			Mxy	,
c		m		c	m		c		m
где m (x, y,z)dv,	Myz		x (x, y,z)dv ,							Mxz y (x, y,z)dv ,

Mxy z (x, y,z)dv.

Отсюда в случае однородного тела, т.е. при (x,y,z)					1, получим
xc 1v	xdv,	yc 1v	ydv,	zc 1v	zdv.

Пример. Найти центр тяжести однородного полушара

:x2 y2 z2 R2, z 0.

Решение. В силу симметрии заключаем, что xc 0, yc 0. Далее

имеем: V 2 R3.
3
		2		2 R					2				R4
Mxy zdv					rcos r							...		.
										sin drd d			4
		0		0	0
	R4			2 R3			3
Следовательно, zc			:					R.
		4		3			8
Перейдем к		вычислению моментов									инерции		тела относительно

координатных осей. Так как квадраты расстояний от точки M(x,y,z) до осей

Ox, Oy, Oz соответственно равны y2 z2, x2 z2,	x2 y2, то получим
следующие формулы:

x (y2 z2) (x,y,z)dv,

y (x2 z2) (x,y,z)dv,

z (x2 y2) (x,y,z)dv.

Аналогично плоскому случаю интегралы

41

xy xy (x,y,z)dv,

yz yz (x,y,z)dv,

zx zx (x,y,z)dv,

называются центробежными моментами инерции. Для полярного момента инерции формула имеет вид:

0 (x2 y2 z2) (x,y,z)dv

Следовательно 2 0 x y z .

Пример: Для однородного шара x2 y2 z2 R2 найти x .

Решение.

x (y2 z2)dv r2 sin2 sin2 r2 cos2 r2 sin drd d ...

415R5 .

КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ. ЗАДАЧИ, ПРИВОДЯЩИЕ К КРИВОЛИНЕЙНЫМ ИНТЕГРАЛАМ

Задача о массе материальной линии. Пусть вдоль некоторой гладкой кривой AB распределена масса с переменной линейной плотностью(M), где M - любая точка кривой AB ( (M) - предел средней плотности распределения вещества на бесконечно малой дуге, содержащей точку M ). Требуется определить массу m дуги AB.

Для решения задачи, раздробим дугу AB на n произвольных частей, предполагая, что на каждой из них плотность постоянна и равна (Nk ) для k -ой части, где Nk - одна из точек этой части, безразлично какая. Тогда масса k -ой части приближенно равна mk (Nk ) lk , (k 1,2,...,n), а масса всей

дуги приближенно равна m n (Nk ) lk , где lk - длина k -ой части. В

k 1

42

пределе при 0 ( max k ) получим точное значение массы всей дуги

AB, т.е. m lim n (Nk ) lk .

0 k 1

Задача, о площади цилиндрической поверхности. Пусть в плоскости xOy дана некоторая гладкая кривая AB и на этой кривой определена непрерывная функция

	f (M) f (x,y) 0.
Непрерывность	f (M) вдоль кривой AB означает, что в любой точке M0
этой кривой	lim f (M) f (M0), где M также точка этой кривой. Тогда
M M0

точки пространства (x,y, f (x,y)) в совокупности составят некоторую кривую, лежащую на цилиндрический поверхности, для которой кривая AB - направляющая, а образующая перпендикулярна к плоскости xOy. Требуется определить площадь части поверхности, которая ограничена сверху кривой z f (x,y), снизу кривой AB, а с боков прямыми AA и BB .

Произвольным образом	разобьем дугу		AB на	n	частей точками
A M0,M1,M2,...,Mn B. Из	каждой	точки дробления			Mk (k 1,2,...,n 1)
проведем перпендикуляры к плоскости		xOy высотой		f (Mk ). В результате
вся цилиндрическая поверхность разобьется на n полосок.
Каждую такую полоску заменим прямоугольником с основанием lk ,
где lk - длина дуги Mk 1Mk (k 1,2,...,n), и			высотой,		равной значению

43

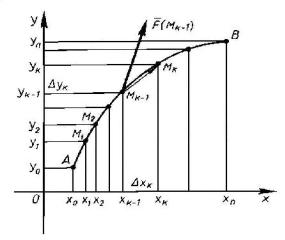
функции f (Nk ), где Nk - одна из точек дуги Mk 1Mk , безразлично какая. На рисунке в целях его упрощения в качестве такой точки взята точка Mk 1. Тогда площадь k -й полоски будет приближенно равна:

Sk f (Nk ) lk ,

а площадь всей поверхности AA'BB': S n f (Nk ) lk .

k 1

При 0 в пределе получим точное значение искомой площади:

S lim

n f (Nk ) lk .

0 k 1

Задача о работе силы. Пусть материальная точка под действием силы

перемещается вдоль непрерывной плоской кривой

AB в направлении от

F

A к B. Сила

предполагается переменной,

зависящей от положения точки

F

на кривой

AB.

Вычислим работу силы

,

затраченную на перемещение

F

точки из

A в

точку B.

С этой

целью разобьем

произвольно точками

A M0,M1,M2,...,Mn B

дугу

AB

на

n

частичных

дуг

M0M1, M1M2,...,Mn 1Mn , с длинами

l1, l2,..., ln .

Наибольшую из длин lk (k 1,2,...,n)						обозначим . Ввиду малости
lk можно приближенно принять, что:
а) вектор силы					сохраняет на дуге	Mk 1Mk постоянное значение,
				F
равное		(Nk ), где Nk	- одна из точек элемента Mk 1Mk , безразлично какая в
	F

целях его упрощения в качестве такой точки взята точка Mk 1;

44

б) дуга Mk 1Mk может быть заменена хордой Mk 1Mk , стягивающей

							_________
концы этого элемента. Вектор Mk 1Mk									равен приращению радиус-вектора
r	(Mk ):	rk	r	(Mk )	r	(Mk 1)	(	rk (xk xk 1,yk yk 1)). Тогда на элементе

дуги Mk 1Mk работа сила F приближенно равна F(Nk ) rk .

Пусть вектор F(M) имеем проекции P(M), Q(M) на

соответствующие оси. Тогда работа силы								вдоль всей дуги AB	будет
							F
приближенно равна n		(Nk )			rk или
	F
k 1
		n P(Nk ) xk Q(Nk ) yk ,							(1)
		k 1
где xk xk xk 1, yk yk yk 1.
Перейдя в сумме (1) к пределу							при 0, получим		точное
выражение работы силы				вдоль всей дуги AB:
			F
	lim n P Nk xk Q Nk yk .								(2)
	0 k 1

ОПРЕДЕЛЕНИЕ КРИВОЛИНЕЙНЫХ ИНТЕГРАЛОВ И ИХ СВОЙСТВА

Из рассмотренных выше двух задач видно, что хотя они имеют различный смысл, но математический аппарат для их решения один и тот же. В этих двух задачах получаем выражение одного и того же вида:

		lim n f (Nk ) lk .	(3)
		0 k 1
Определение. Если существует предел (3) не зависящий от способа
деления дуги	AB на частичные дуги и выбора точек		Nk , то он называется
криволинейным интегралом первого рода от функции			f (M) по дуге ABи
обозначается	f (M)dl или	f (x,y)dl .
	AB	AB

45

Дуга AB называется путем интегрирования, точка A - начальной, а точка B - конечной точками интегрирования.

Сумма n f (Nk ) lk называется интегральной суммой.

k 1

Рассмотренные первые две задачи показывают:

а) криволинейный интеграл первого рода при f (M) 0 ( f (M)на дуге AB непрерывен) численно равен площади участка цилиндрической поверхности с образующей, параллельной оси Oz. Снизу этот участок ограничен дугой AB, а с верху - кривой, изображающей подынтегральную

функцию	z f (M). В	этом	состоит геометрический смысл интеграла
первого рода.
б)	криволинейный	интеграл		(M)dl	( (M)-линейная	плотность)
				AB
равен массе m материальной			дуги	AB. В	этом состоит его	физический

смысл. Отсюда следует, что интеграл dl численно равен длине дуги AB.

AB

Хотя криволинейный интеграл первого рода непосредственно сводится к определенному интегралу, между этими понятиями есть и следующее различие: в выражении (3) величины lk обязательно положительны, независимо от того, какую точку кривой AB считать начальной, а какую конечной. Поэтому

f (M)dl f (x,y)dl .

AB BA

Решение задачи о работе силы сводится к вычислению предела вида

(2). К вычислению подобного рода пределов приводят и другие задачи. Поэтому будем рассматривать выражение

lim n	P Nk xk Q Nk yk ,	(4)
0 k 1

(здесь P(M), Q(M)- проекции вектор – функции a(M), определенной на дуге AB, на оси координат).

46

Определение. Если существует предел (4), не зависящий от способа деления дуги AB на частичные дуги и выбора точек Nk , то он называется

криволинейным интегралом					второго	рода от	векторной функции
							adr	или Pdx Qdy.
a(M) P(M)i		Q(M)j по дуге AB и обозначается
							AB	AB
Сумма
				n	P Nk xk	Q Nk yk		(5)
				k 1

называется интегральной суммой.

Физическое истолкование криволинейного интеграла второго рода, например, как следует из рассмотренной задачи в предыдущем пункте - это работа силы a(M) вдоль дуги AB.

Если Q(x,y) 0	(P(x,y) 0), то интеграл второго рода имеет вид:
	P(x,y)dx,				(6)
			Q(x,y)dy
	AB	AB

иназывается криволинейным интегралом по координате x (y).

Вотличие от криволинейного интеграла первого рода криволинейный интеграл второго рода зависит от того, в каком направлении от A к B или от B к A пробегает кривая AB (кратко L), и меняет знак при изменении направления обхода кривой.

Вслучае, когда L - замкнутая кривая, т.е. когда точка B совпадает с A, из двух возможных направлений обхода замкнутого контура L условимся

называть положительным, то при котором область, лежащая внутри этого контура, остается слева по отношению к точке, совершающей обход. Противоположное направление обхода контура L условимся называть отрицательным.

Криволинейный интеграл второго рода по замкнутому контуру L, пробегаемому в положительном направлении, часто обозначают символом:

P(x,y)dx Q(x,y)dy

L

47

Имеет место следующая зависимость между криволинейными интегралами первого и второго рода:

a(M)dr a (M)dl ,

AB AB

где (M) - единичный вектор касательной к дуге AB в точке M и соответствующий направлению дуги от A к B:

a (M) a(M) cos a^ - проекция вектора a(M) на эту касательную.

Так же как в случае определенных интегралов двух родов устанавливаются следующие три свойства, общие криволинейным интегралам первого и второго рода:

1)постоянный множитель можно выносить за знак криволинейного интеграла;

2)криволинейный интеграл от алгебраической суммы конечного числа функций равен такой же сумме криволинейных интегралов от слагаемых;

3)если путь интегрирования разбит на конечное число частей, то криволинейный интеграл по всему пути равен сумме криволинейных интегралов по всем его частям.

Заметим, что кривая AB может быть и замкнутой. Справедливо и еще одно свойство, общее для обоих криволинейных интегралов:

4)криволинейный интеграл вдоль замкнутого контура не зависит от выбора начальной точки на этом контуре.

ВЫЧИСЛЕНИЕ КРИВОЛИНЕЙНЫХ ИНТЕГРАЛОВ

Пусть гладкая	дуга AB задана параметрически уравнениями
x x(t), y y(t) ( t	) и функции f (x,y), P(x,y), Q(x,y) определены и

непрерывны на этой дуге.

Для вычисления криволинейного интеграла первого рода имеем формулу:

f (x,y)dl f x(t),y(t)		x'2 (t) y'2 (t)	dt .	(7)
AB

48

В частности, если дуга

AB задана уравнением

y y(x)

на отрезке [a;b],

то

согласно формуле (7) имеем:

b

x,y(x)

f (x,y)dl f

1 y'2

dx.

(8)

AB

a

Для вычисления криволинейного интеграла второго рода имеем

формулу при параметрическом задании функции:

Pdx Qdy (Px' Qy')dt .

(9)

AB

В частности, если дуга

AB задана уравнением

y y(x)

на отрезке [a;b],

то

аналогично формуле (8) из (9) имеем:

b

(10)

Pdx Qdy (P(x,y(x)) Q(x,y(x))y

(x))dx.

AB

a

Пример 1. Вычислить криволинейный интеграл

(x y)dl , если путь

OA

от O(0,0) до A(4,3) - отрезок прямой.

Решение. Из уравнения прямой проходящей через заданные две точки

x 0

y 0

3

3

9

имеем:

откуда

3x 4y или

y 4 x,

y' 4, y 2

и

по

4 0

3 0

16

формуле (8) имеем:

4

3

4

x

5

4

5 x2

4

5 16

5

9

25

(x y)dl x

x

1

dx

dx

xdx

.

4

16

4

16

16

16 2

16 2

2

AB

0

0

0

0

Пример 2. Вычислить криволинейный интеграл

xdy ydx, если OA -

OA

дуга параболы y x2, O(0,0),

A(2,4).

Решение. Из y x2 имеем dy 2xdx. По формуле (10) имеем:

xdy ydx

2 x 2xdx x2dx

2

2x2 x

2 dx 2 x2dx

x3

|2

8

3

0

3

OA

0

0

0

Все сказанное о криволинейных интегралах для плоских кривых можно перенести и на пространственные кривые.

49

По аналогии со случаем плоской кривой можно определить

криволинейный интеграл первого рода f (x,y,z)dl и криволинейные

AB

интегралы второго рода

P(x,y,z)dx,	Q(x,y,z)dy,	R(x,y,z)dz,
AB	AB	AB

P(x,y,z)dx Q(x,y,z)dy R(x,y,z)dz .

AB

Техника вычисления таких интегралов, по существу, ничем не отличается от техники вычисления соответствующих интегралов по плоской кривой.

ФОРМУЛА РИМАНА-ГРИНА

Пусть функции P(x,y), Q(x,y) непрерывны вместе со всеми

частными производными Py' (x,y) и Qx' (x,y) в замкнутой области G, граница

L которой пересекается прямыми параллельными осям координат, не более чем в двух точках. Тогда формула

	Q		P
					P(x,y)dx Q(x,y)dy	(11)
	x		dxdy
G			y	L

называется формулой Римана-Грина. Эта формула устанавливает связь между двойным и криволинейным интегралами.

Пример. С помощью формулы Римана-Грина вычислить

криволинейный	интеграл	(x y)dx (x y)dy,			где	L-	окружность
		L
x2 y2 R2.
Решение.	P(x,y) x y , Q(x,y) x y , P' (x,y) 1					, Q'	(x,y) 1.
				y		x
Тогда по формуле (11) имеем:
					2	R
(x y)dx (x y)dy 1 1 dxdy 2 dxdy 2						d rdr
L		G		G	0	0
	2 |2 r2		|R 2 2	R2 2 R2.
	0	2	0	2

50