lektsia_2_kurs_ITF

ПОВЕРХНОСТНЫЕ ИНТЕГРАЛЫ ОПРЕДЕЛЕНИЕ ПОВЕРХНОСТНОГО ИНТЕГРАЛА 1-ГО РОДА

Задача о массе изогнутой пластины. Пусть на поверхности непрерывно распределено с известной плотностью (M). При этом под плотностью вещества в точке M поверхности понимается предел средней плотности на бесконечно малом элементе, содержащем точку M . Требуется определить всю массу материальной поверхности .

Разделим поверхность произвольными гладкими линиями на n частей 1, 2,..., n без общих внутренних точек с площадями s1, s2,..., sn ; наибольшую из этих площадей обозначим через . Предположим, что в каждой части k плотность постоянна и равна (Nk ), где Nk - одна из точекk , безразлично какая. Тогда масса k -го элемента будет приближенно равна

mk (Nk ) sk .

Для массы всей поверхности получим приближенное выражение

m n (Nk ) sk .

k 1

За массу материальной поверхности (изогнутой пластины) естественно принять предел полученной суммы при стремлении к нулю:

m lim n (Nk ) sk

0 k 1

Сформулируем определение поверхностного интеграла первого рода в общем случае. Пусть функция f (M) f (x,y,z) определена на гладкой или кусочно-гладкой поверхности . Поверхность называется гладкой, если в каждой ее точке существует касательная плоскость и при переходе от точки к точке положение этой касательной плоскости меняется непрерывно; поверхность, состоящая из конечного числа гладких кусков, которые соединены непрерывно, называется кусочно-гладкой. Разделим, как и выше,на n частей. Выберем на каждой частичной поверхности произвольную точку Nk и составим интегральную сумму

51

n	f (Nk ) sk .	(1)
k 1

Определение. Предел интегральной суммы (1) при стремлении к нулю (если он существует и не зависит от способа деления на частичные поверхности и от выбора точек Nk , называется поверхностным интегралом первого рода от функции f (M)) по поверхности и обозначается символом

f (M)ds или f (x,y,z)ds

Его физический смысл, это масса материальной поверхности с плотностью распределения вещества f (M). Данное определение, по сути дела, аналогично определению двойного интеграла. Поэтому теорема существования двойного интеграла и его свойства без особых изменений переносится на поверхностные интегралы первого рода. В частности, если на

поверхности f (x,y,z) 1, то S ds - площадь поверхности .

ВЫЧИСЛЕНИЕ ПОВЕРХНОСТНОГО ИНТЕГРАЛА 1-ГО РОДА

Пусть	поверхность	задана уравнением		z z(x,y), где	функция
z(x,y) вместе с производными zx (x,y) и			zy (x,y)	непрерывна в замкнутой
области G -	проекции	на плоскость	xOy, и пусть функция		f (x,y,z)

непрерывна на поверхности и, следовательно, интегрируема по поверхности . Тогда будем иметь для вычисления поверхностного интеграла следующую формулу:

f (x,y,z)ds f (x,y,z(x,y))

1 zx

2(x,y) zy

2(x,y)

dydx.

(2)

G

Аналогично получаются формулы, выражающие поверхностный интеграл первого рода по поверхности через двойные интегралы по ее проекции на плоскости yOz и xOz.

Пример. Вычислитьинтеграл

52

I 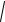1 4x2 4y2 dS ,

где - часть поверхности параболоида вращения z 1 x2 y2, отсеченная плоскостью z 0.

Решение. Нарисуемповерхность

z 1 x2 y2, zx 2x, zy 2y.

Следовательно, по формуле (2) имеем:

I 1 4x2 4y2 1 4x2 4y2dxdy (1 4x2 4y2)dxdy.

G

Переходя к полярным координатам, получим:

	2	1
I (1 4x2	4y2)dxdy d (1 4r2)rdr ... 3 .
	0	0

ОПРЕДЕЛЕНИЕ ПОВЕРХНОСТНОГО ИНТЕГРАЛА 2-ГО РОДА

Пусть - некоторая ориентируемая поверхность, заданная уравнением z f (x,y), и пусть R(x,y,z) - функция, определенная в точках поверхности. Выберем одну из двух сторон поверхности, т.е. выберем одну из двух возможных направлений векторов нормали в точках поверхности (тем самым мы ориентировали поверхность). Если векторы нормалей составляют острые углы с осью Oz, то будем говорить, что выбрана верхняя сторона поверхности z f (x,y), если тупые углы, то нижняя сторона поверхности. Разобьем поверхность произвольно на n частей, не имеющих общих

53

внутренних точек. Обозначим через k проекцию k -й части поверхности на плоскость xOy. Выбрав на каждой частичной поверхности произвольную точку Nk ( k , k , k ), составим сумму:

n	R( k , k , k ) k ,	(3)
k 1

где k - площадь k , взятая со знаком «+», если выбрана верхняя поверхности , и со знаком «-», если выбрана нижняя поверхности .

Обозначим через наибольший из диаметров частей поверхности и дадим следующее определение.

Определение. Предел интегральной суммы (3) при 0 (если он существует и не зависит от способа деления на частичные поверхности выбора точек Nk ) называется поверхностным интегралом второго рода от функции R(x,y,z) по выбранной стороне поверхности и обозначается одним из символов

R(M)dxdy или R(x,y,z)dxdy.

Аналогичным образом определяются поверхностные интегралы второго рода:

P(x,y,z)dydz или Q(x,y,z)dxdz.

Сумму P(x,y,z)dydz+ Q(x,y,z)dxdz+ R(x,y,z)dxdy принято

называть общим поверхностным интегралом второго рода и обозначать символом

P(x,y,z)dydz Q(x,y,z)dxdz R(x,y,z)dxdy.	(4)

Поверхностный интеграл второго рода обладает всеми свойствами поверхностного интеграла первого рода, за исключением одного: при изменении стороны поверхности (переориентации) интеграл меняет знак.

54

ВЫЧИСЛЕНИЕ ПОВЕРХНОСТНОГО ИНТЕГРАЛА 2-ГО РОДА

Пусть ориентированная (выберем верхнюю сторону) гладкая поверхность задана уравнением z f (x,y), где f (x,y) - функция, определенная в замкнутой области G - проекции поверхности на плоскость xOy, а R(x,y,z) - непрерывная функция на поверхности . Тогда для вычислений поверхностного интеграла второго рода имеем формулу

R(x, y,z)dxdy = R(x,y, f (x,y))dxdy.			(5)
	G
Если выбрать нижнюю сторону поверхности, то перед интегралом в
правой части (5) получим знак «-».
Аналогично вычисляются интегралы
	P(x,y,z)dydz ,	Q(x,y,z)dxdz.
Для вычисления интеграла общего вида (4) используются формулы

указанных трех интегралов, если поверхность однозначно проецируется на все три координатные плоскости.

Пример. Вычислить интеграл (y2 z2)dxdy , где			- верхняя
сторона поверхности z
	1 x2	, отсеченная плоскостями y 0,	y 1.
Решение.

Проекцией на плоскость xOy будет прямоугольник G : 1 x 1, 0 y 1. Тогда по формуле (5) имеем:

55

		1	1
(y2	z2)dxdy (y2	1 x2) dx (y2 1 x2)dy ... 2.
		1	0

УРАВНЕНИЯ И ЗАДАЧИ МАТЕМАТИЧЕСКОЙ ФИЗИКИ ОСНОВНЫЕ ПОНЯТИЯ О ДУЧП ВТОРОГО ПОРЯДКА Определение. Дифференциальным уравнением с частными

производными называется равенство, связывающее неизвестную функцию от нескольких независимых переменных, эти переменные и частные производные от неизвестной функции по независимым переменным.

Определение. Порядком дифференциального уравнения с частными производными называется порядок старшей частной производной, входящей в это уравнение.

Определение. Если u u(x,y), то в общем случае дифференциальное уравнение с частными производными второго порядка имеет вид:

	u		u			2	u				2	u				2	u
		,		,					,					,					0,	(1)
								2					2
F x,y,u,	x		y		x					y
															x y

где F - известная функция.

Определение. ДУЧП называется линейным, если оно линейно относительно неизвестной функции и всех ее частных производных.

Для физических приложений особый интерес представляют линейные дифференциальные уравнения с частными производными второго порядка.

Для случая двух независимых переменных приведем важнейшие типы таких уравнений:

1. Волновое уравнение

	2u	a2	2u	.	(2)
	t2		x2

Это уравнение встречается при изучении ряда колебательных процессов (поперечные колебания упругой струны, колебание газа в трубке и др.).

2. Уравнение теплопроводности (уравнение Фурье),

56

	u	a2	2u	,	(3)
	t		x2

описывающее процессы распределения тепла и т.д. 3. Уравнение Лапласа

	2u		2u	0.	(4)
	x2		y2

К исследованию этого уравнения приводят рассмотрение задач об электрических магнитных полях, о стационарном состоянии, задач гидродинамики, диффузии и т.д.

Для решения этих уравнений в различных условиях были созданы специальные приемы (так называемые «методы математической физики»).

Определение. Решением уравнения (1) называется всякая функция u (x,y), обращающая уравнение (1) в тождество.

Как известно, общие решения обыкновенных дифференциальных уравнений содержат произвольные постоянные. Для ДУЧП их общие решения включают произвольные функции.

КЛАССИФИКАЦИЯ ЗАДАЧ МАТЕМАТИЧЕСКОЙ ФИЗИКИ

Как уже отмечали, ДУЧП имеют бесконечное множество решений. Поэтому в этом случае, когда физическая задача приводится к уравнению с частными производными, для однозначной характеристики процесса необходимо к уравнению присоединить некоторые дополнительные условия.

Для задач, приводящих к уравнениям (2), (3), дополнительные условия разделяются на начальные и краевые.

Начальные условия состоят в задании в один какой-нибудь момент времени, с которого начинается изучение данного физического явления (обычно при t 0) значений искомой функции и ее производной (в случае уравнения (2)) или только значений самой функции (в случае уравнения (3)).

Краевые (или граничные) условия для этих задач заключаются в том, что указываются значения неизвестной функции u(x,t) на площадь

57

интервала изменения координаты x. Если процесс протекает в бесконечном интервале изменения координаты x (бесконечная струна, бесконечный стержень), то краевые условия отпадают, и получается задача только с начальными условиями, или, как ее часто называют, задача Коши.

Если ставится задача для конечного промежутка, то должны быть заданы и начальные и краевые условия. Тогда говорят о смешанной задаче.

Например, рассмотрим простейшую задачу о поперечных колебаниях струны, закрепленной на концах. В этой задаче u(x,t) дает отклонение струны от оси Ox. Если концы струны 0 x l закреплены, то должны выполняться краевые условия

	u |x 0 0,	u |x l 0	(5)
или, более кратко, u(0,t) 0,	u(l,t) 0.

Краевые условия (5), где правые части-нули, называются однородными.

Однако заданием только этих краевых условий закон колебания не определяется однозначно. Он будет зависеть еще и от начальной формы струны, и от начальной скорости струны в каждой точке. Итак, кроме краевых условий, должны быть заданы следующие начальные условия

u(x,0) f (x), ut (x,0) F(x).

Здесь f (x) и F(x) - известные, заранее заданные функции: первая из них в качестве графика имеет форму струны в начальный момент, вторая указывает, какова в начальный момент скорость каждой точки струны.

Переходя к уравнению (4), заметим, что в это уравнение время t не входит и обе независимые переменные являются координатами точки. Для задач, приводящих к уравнению (4), ставятся только краевые условия, т.е. указывается поведение неизвестной функции на контуре области.

Кроме того, следует иметь в виду, что каждая из выведенных уравнений носит идеализированный характер, т.е. отражает лишь наиболее существенные черты соответствующего физического процесса. Данные,

58

входящие как в уравнение, так и в дополнительные условия в физической задачи, определяются из экспериментальных данных и могут считаться известными лишь приближенно. Поэтому мы должны быть уверенными в том, что решение задачи при приближенных исходных данных будет близко к тем решениям, которые получились бы при точных исходных данных. Таким образом, важно, чтобы малые изменения данных задачи вызывали лишь малые изменения в ее решении, то, как говорят, чтобы решение было устойчиво относительно исходных данных.

Задача считается поставленной правильно (корректно), если решение задачи, удовлетворяющее всем ее условиям, существует, единственно и устойчиво. Все задачи, которые мы будем рассматривать в дальнейшем, являются корректными.

ЗАДАЧА КОШИ. МЕТОД ДАЛАМБЕРА

Рассмотрим задачу о колебаниях бесконечной струны. Если струна очень длинная, то на колебания, возникающие где-то в ее середине, концы струны будут оказывать малое влияние. Поэтому, рассматривая свободные колебания неограниченной струны, мы должны решить уравнение

	2u	a	2	2u		(6)
	t2			x2
только при начальных условиях
u(x,0) f (x),						(7)
ut (x,0) F(x),						(8)
причем ввиду неограниченности струны функции						f (x)и F(x) заданы на

всей числовой оси.

Такая задача, называется задачей с начальными условиями или задачей Коши. Метод ее решения, называется методом Даламбера или методом бегущих волн.

59

Заметем, что если (p) и (q), где p и q - произвольные независимые переменные – любые дважды дифференцируемые функции, то функция

u(x,t) (x at) (x at)

(9)

является решением уравнения (6).

Решение (9), зависящее от двух произвольных функций, называется решением Даламбера.

Используя начальные условия (7) и (8), получим решение (6) в виде

		f (x at) f (x at)		1	x at
	u(x,t)				F(y)dy.	(10)
		2		2a
					x at

Формула (10) называется формулой Даламбера.

В случае бесконечного стержня краевые условия отсутствуют и задача Коши сводится к отысканию решения уравнения

ut a2 x2u2 ,

определенного для всех x, x	и t 0, и удовлетворяющую
начальному условию

u(x,0) f (x).

Это решение имеет вид:

		1					(x s)2
							2
u(x,t)					f (s)e		4a	t	ds.
2		a2t

Последняя формула была получена в 1823 году Симеоном Пуассоном.

РЕШЕНИЕ СМЕШАННОЙ ЗАДАЧИ МЕТОДОМ ФУРЬЕ

Рассмотрим волновое уравнение

	2u	a2	2u		(11)
	t2		x2
при краевых условиях
u(0,t) 0,			u(l,t) 0		(12)

60