lektsia_2_kurs_ITF

npn const .

Отсюда pn n .

Исходя из формулы Бернулли, для вероятности появления события A в n-й серии ровно m раз имеем выражение

P

m C

m

p

m

1 p

n m

C

m

m

n m

1

.

n

n

n

n

n n

n

При фиксированном m имеем:

lim P

m

m e .

n

n

m!

Отсюда при больших n для искомой вероятности Pn m имеем приближенную формулу Пуассона

Pn m mm! e , где npn .

Пример. Завод отправил на базу 500 доброкачественных изделий. Вероятность того, что в пути изделие повредится, равна 0,002. Найти вероятность того, что на базу прибудут 3 негодных изделия.

Решение. По условию n 500, pn 0,002, m 3. Поэтому

500 0,002 1.

Тогда искомая вероятность равна

P500 3 31!e 1 0,06.

Определение. Говорят, что случайная величина X распределена по закону Пуассона, если эта величина задана таблицей

X		0	1		2			3	…
p		e	e	2	e		3	e	…
				2!			3!
где		- фиксированное положительное число.

Математическое ожидание и дисперсия определяются соответственно

M X , D X .

81

ЛОКАЛЬНАЯ И ИНТЕГРАЛЬНАЯ ПРЕДЕЛЬНЫЕ ТЕОРЕМЫ ЛАПЛАСА

Если число испытаний n велико, то вычисления по формуле Бернулли становятся затруднительными. Лаплас получил важную приближенную формулу для вероятности Pn m появление события A точно m раз, если n достаточно большое число.

Локальная предельная	теорема	Лапласа. Пусть p p A -
вероятность события A, причем	0 p 1.	Тогда вероятность того, что в

условиях схемы Бернулли событие A при n испытаниях появится точно m раз, выражается приближенной формулой Лапласа:

1

np

P

m

m

,

(2)

n

npq

npq

где

q 1 P, x

1

e 2x2 .

2

Для функции x имеется таблица ее значении для положительных

значений x. Функция x четная.

Пример. Вероятность

поражения

цели стрелком при

одиночном

выстреле равна p 0,2. Какова вероятность того, что при 100 выстрелах цель будет поражена ровно 20 раз?

Решение. Здесь p 0,2, q 0,8, n 100, m 20.

	Отсюда								4,	m np				20 100 0,2	0.
		npq			100 0,2 0,8
											npq			4
	Учитывая 0			1				0,4 из формулы (2) получаем:
						2

P100 20 0,40 1/4 0,1.

Интегральная предельная теорема Лапласа. Поставим следующий вопрос: какова вероятность того, что в условиях схемы Бернулли событие A, имеющее вероятность p A p 0 p 1 , при n испытаниях появится

82

не менее k раз и не более l раз? Эту искомую вероятность обозначим через

Pn k,l .

Введем функцию

	x		1			t2
					e 2 dt		(3)
			2
				0

называемую функцией Лапласа или интегралом вероятностей. Очевидно,x есть первообразная для функции x . Т.к. x 0 в ; , то x - возрастающая функция в этом интервале. Поэтому на основании формулы Ньютона-Лейбница имеем:

Pn k,l xl xk ,

(4)

где

x

k

np

,

x

l

np

.

k

nPq

l

npq

(4) называется интегральной формулой Лапласа.

Как известно, интеграл e	x2
	2 dx не берется в элементарных функциях.

Поэтому для функции (3) составлена специальная таблица ее специальных значений x, функция x нечетная и 0 0.

Пример. Вероятность того, что изделие не прошло проверку ОТК, равно 0,2. Найти вероятность того, что среди 400 случайно отобранных изделий окажутся непроверенными от 70 до 100 изделий.

Решение. Здесь n 400, k 70, l 100,								p 0,2, q 0.8.
Поэтому
x			70 400 0,2			1,25,	x	100		400 0,2	2,5.
	k			400 0,2 0,8			l	400		0,2 0,8

Тогда

P400 70,100 2,5 1,25 2,5 1,250,4938 0,3944 0,8882.

83

НЕПРЕРЫВНЫЕ СЛУЧАЙНЫЕ ВЕЛИЧИНЫ ИНТЕГРАЛЬНАЯ ФУНКЦИЯ РАСПРЕДЕЛЕНИЯ

Для непрерывной случайной величины, в отличие от дискретной, нельзя построить таблицу распределения. Поэтому непрерывные случайные величины изучаются другим способом.

Пусть X - непрерывная случайная величина с возможными значениями из некоторого интервала a;b и x - действительное число. Под выражением X x понимается событие «случайная величина X приняла значение, меньшее x». Вероятность этого события P X x есть некоторая функция переменной x:

	F x P X x .
Определение.	Интегральной	функцией	распределения	или
интегральным законом распределения непрерывной случайной величины X
называется функция	F x , равная	вероятности	того, что X приняла
значение, меньшее x:
	F x P X x .			(1)

Интегральная функция распределения совершенно также определяется и для дискретных случайных величин.

Свойства. 1) 0 F x 1.

2)F x - неубывающая функция, т.е. если x1 x2, то F x1 F x2 .

3)Вероятность попадания случайной величины X в полуинтервал

a,b равна разности между значениями интегральной функции распределения в правом и левом концах интервала a,b :

P a X b F b F a .

(2)

Пример. Случайная величина X задана интегральной функцией распределения:

84

0,					x 1,
				1
x
F x					, 1 x 3,.
	4			4
					x 3.
1,

Найти вероятность того, что в результате испытания							X	примет значение,
принадлежащее полуинтервалу 0,2 .
Решение. Так как на полуинтервале 0,2			F x		x		1	, то
				4			4
P 0 X 2 F 2 F 0		1	1	1			1.
		2	4	4			2
Случайную величину X	будем	называть					непрерывной, если
непрерывна ее интегральная функция распределения F x .
4) Вероятность того, что непрерывная случайная величина X примет
какое-либо заранее заданное значение, равна нулю:
P X x1 0.								(3)
5) Вероятность попадания	непрерывной			случайной величины в

интервал, сегмент и полуинтервал с одними и теми же концами одинаковы:

P a X b P a X b P a X b P a X b .

(4)

6) Если возможные значения случайной величины X принадлежат интервалу a;b , то:

1)F x 0, при x a;

2)F x 1, при x b.

Следствие. Если возможные значения непрерывной случайной величины расположены на всей числовой оси, то справедливы следующие предельные соотношения:

F lim F x 0,

x

F lim F x 1.

x

85

ДИФФЕРЕНЦИАЛЬНАЯ ФУНКЦИЯ РАСПРЕДЕЛЕНИЯ Определение. Дифференциальной функцией распределения

непрерывной случайной величины X (или ее плотностью распределения) называется функция f x , равная производной интегральной функции распределения:

f x F x .
Так как F x - неубывающая функция, то	f x 0.
Теорема. Вероятность попадания непрерывной случайной величины
X в интервал a,b равна определенному	интегралу от ее	плотности
вероятности, взятому в пределах от a до b:
b
P a X b f x dx .		(5)

a

Следствие. В частности, если f x - четная функция и концы интервала симметричны относительно начала координат, то

				a
P a X a P		x		a 2 f x dx.	(6)
0

Пример. Задана плотность вероятности случайной величины X

0,	x 0,
	0 x 1,
f x 2x,
	x 1.
0,

Найти вероятность того, что в результате испытание X примет значение, принадлежащее интервалу (0,5;1).

Решение. Согласно формуле (5) имеем:

1

P 0,5 X 1 2xdx x2 10,5 0,75.

0,5

Если заменить a на , b на x , то получим

x

F x F f x dx.

Откуда в силу F 0, имеем:

86

x
F x f x dx.	(7)

Формула (7) дает возможность отыскать интегральную функцию распределения F x по ее плотности вероятности.

Из формулы (7) вытекает, что

f x dx 1.	(8)

МО И ДИСПЕРСИЯ НЕПРЕРЫВНОЙ СЛУЧАЙНОЙ ВЕЛИЧИНЫ Определение 1. Математическим ожиданием непрерывной случайной

величины X с плотностью вероятности f x	называется величина
несобственного интеграла (если он сходится):
M x xf x dx.	(9)

Определение 2. Дисперсией непрерывной случайной величины X , математическое ожидание которой M x a и функция f x является ее плотностью вероятности, называется величина несобственного интеграла (если он сходится):

D x x a 2 f x dx.	(10)
Математическое ожидание и дисперсия непрерывной	случайной

величины имеют те же свойства, что и математическое ожидание и дисперсия дискретной случайной величины.

Для непрерывной случайной величины X среднее квадратическое отклонение определяется, так же как и для ДСВ, формулой 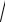x D x .

Пример. Случайная величина X задана плотностью вероятности

87

0,			x 0,
x
f x			, 0 x 2,
	2
			x 2.
0,

Найти M x , D x и x .

Решение.

		2 x			1	2	2				x3						4
															2
M x xf x dx				xdx	2	x		dx							0		3.
			2								6
		0				0
	2				2				4	2	x						2
D x	x M x	f x dx				x							dx					.
									3		2						9
					0

x D x 92 32 0,47.

РАВНОМЕРНОЕ РАСПРЕДЕЛЕНИЕ

Распределение вероятностей непрерывной случайной величины X , принимающей все свои значения из отрезка a,b , называется равномерным, если ее плотность вероятности f x на этом отрезке постоянна, а вне его равна нулю, т.е.

			0,	x a,
		f x	c,	a x b,
				x b.
			0,
	Отсюда
			b
		f x dx cdx c b a ,				(11)
			a
	но как известно f x dx 1.
	Сравнивая последние два интеграла, получаем что c				1	.
					b a

График функции f x выглядит следующим образом

88

	Найдем интегральную функцию F x .
1)	Если x a, то	f x 0, следовательно, F x 0.
2)	Если a x b, то		f x 1/ b a , и, следовательно,
			x		1					x a
			F x					dx			.
				b a
			a							b a
3)	Если b x, то	f x 0,, и, следовательно,
				b	1
			F x						dx 1.
						b a
				a

Тогда графиком F x является

МО равномерно распределенной непрерывной случайной величины находится по формуле

M X 12 a b ,

а дисперсия по формуле

D x b12a 2 .

89

НОРМАЛЬНЫЙ ЗАКОН РАСПРЕДЕЛЕНИЯ

Закон распределения вероятностей непрерывной случайной величины X называется нормальным или законом Гаусса, если ее плотность вероятности есть

f x		1			e	x a 2
						2 2 ,	(12)
			2

где и a - постоянные числа, причем 0.

Математическое ожидание нормального закона распределения равна

M x a,

а дисперсия

D x 2.

Графиком (12) является

Нормальное распределение с параметрами a 0, 1 называется нормированным. Плотность вероятности в случае такого распределения будет

x

1

e

x2

2

.

2

Пусть случайная величина X

распределена по нормальному закону.

Тогда вероятность того, что X примет значение, принадлежащее интервалу

; будет равна

1

x a 2

P x

e

2 2 dx

2

90