
- •Задачи по теории вероятностей и математической статистике
- •Содержание
- •Введение
- •Раздел 1. Теория вероятностей Комбинаторные формулы
- •Классическое определение вероятности
- •Теоремы алгебры событий
- •Свойства функции распределения
- •Свойства математического ожидания
- •Непрерывная случайная величина и её характеристики
- •Законы распределения случайных величин
- •Предельные теоремы теории вероятностей
- •Предельные формулы для схемы Бернулли
- •Раздел 2. Математическая статистика Обработка результатов опытов
- •Точечные оценки неизвестных параметров и методы их получения
- •Интервальные оценки неизвестных параметров
- •Проверка статистических гипотез
- •Сглаживание опытных данных методом наименьших квадратов
- •Ошибки прямых и косвенных измерений
- •Задания для самостоятельной работы студентов
- •Пример выполнения заданий самостоятельной работы студентов Пример выполнения задачи 1
- •Пример выполнения задачи 2
- •Пример выполнения задачи 3
- •Пример выполнения задачи 4
- •Пример выполнения задачи 5
- •Пример выполнения задачи 6
- •Пример выполнения задачи 11
- •Пример выполнения задачи 12
- •Пример выполнения задачи 13
- •Пример выполнения задачи 14
- •Пример выполнения задачи 15
- •Пример выполнения задачи 16
- •Пример выполнения задачи 17
- •Пример выполнения задачи 18
- •Пример выполнения задачи 19
- •Пример выполнения задачи 20
- •Пример выполнения задачи 21
- •Пример выполнения задачи 22
- •Пример выполнения задачи 23
- •Пример выполнения задачи 24
- •Пример выполнения задачи 25
- •Литература
Пример выполнения задачи 20
Условие.
По данной выборке признака
![]() найти выборочную среднюю, исправленную
дисперсию и моду. Построить полигон
(гистограмму) частот, если
найти выборочную среднюю, исправленную
дисперсию и моду. Построить полигон
(гистограмму) частот, если
-

1-4
4-7
7-10
10-13
13-16
16-19
19-22

4
8
12
35
14
12
8
Решение.
Для расчета выборочной средней,
исправленной дисперсии и моды преобразуем
интервальный вариационный ряд в
дискретный. Для этого заменим интервал
![]() на его среднее значение
на его среднее значение![]() .
.
Получим
-

2,5
5,5
8,5
11,5
14,5
17,5
20,5

4
8
12
35
14
12
8
Находим выборочную
среднюю:
![]() ,
,
 .
.
Исправленная дисперсия равна:
 .
.
Мода
![]() равна значению варианты, имеющей
наибольшую частоту, т. е.
равна значению варианты, имеющей
наибольшую частоту, т. е.![]() .
.
Построим гистограмму
частот:
![]() .
.
Заполним таблицу
-

1-4
4-7
7-10
10-13
13-16
16-19
19-22

4
8
12
35
14
12
8
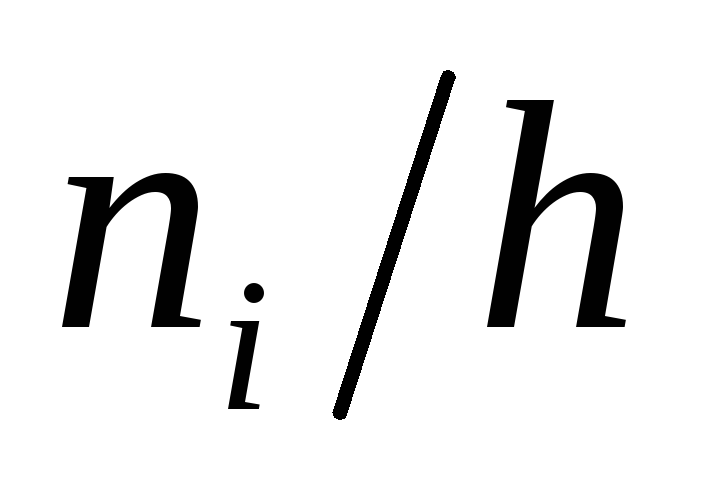
4/3
8/3
4
35/3
14/3
4
8/3
Гистограмма изображена на рисунке 6.

Рис. 6
Ответ.
![]() ,
,![]() ,
,![]() ,
рисунок 6.
,
рисунок 6.
Пример выполнения задачи 21
Условие. На
плоскости даны 6 точек, координаты
которых занесены в таблицу. Пусть
случайная величина
![]() – абсцисса точек, а случайная величина
– абсцисса точек, а случайная величина![]() – ордината. Найти коэффициент линейной
корреляции. Написать уравнения линейной
регрессии
– ордината. Найти коэффициент линейной
корреляции. Написать уравнения линейной
регрессии![]() на
на![]() и
и![]() на
на![]() ,
если
,
если
-

0,4
1,2
1,8
2,5
2,9
3,2

-0,1
-1,1
-1,9
-2,9
-3,3
-3,7
Решение. Коэффициент линейной корреляции определяется формулой:
 ,
,
где
![]() ,
, ,
, ,
,
 ,
,
 .
.
Получим
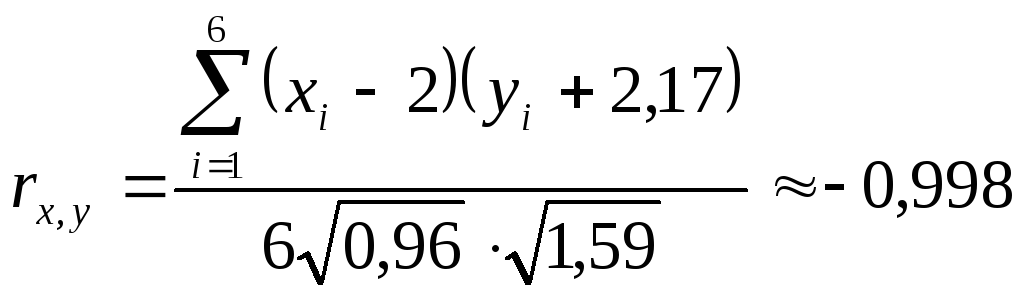 .
.
Напишем уравнения линейной регрессии
![]() на
на
![]() :
:![]() ,
,
получим
![]() или
или![]() .
.
![]() на
на
![]() :
:![]() ,
,
получим
![]() или
или![]() .
.
Ответ.
![]() ,
,![]() ,
,![]() .
.
Пример выполнения задачи 22
Условие.
На плоскости даны 5 точек, координаты
которых занесены в таблицу. Найти
функциональную зависимость
![]() ,
используя метод наименьших квадратов,
если
,
используя метод наименьших квадратов,
если
-

-2,3
-1,7
-0,5
0,7
1,5

5,8
3,9
0,3
-3,2
-6,0
Решение.
Будем искать функциональную зависимость
в виде
![]() ,
где параметры
,
где параметры![]() и
и![]() находим
из системы
находим
из системы
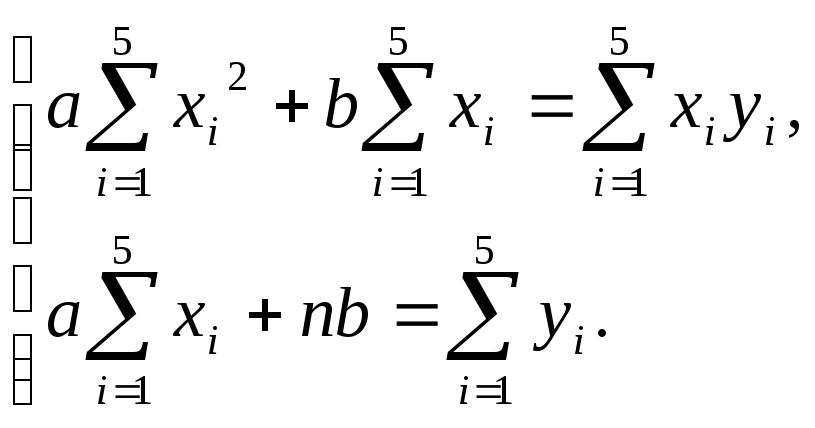
Вычислим
![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
Решаем систему

Параметры равны:
![]() ,
,![]() .
.
Тогда функциональная
зависимость имеет вид:
![]() .
.
Ответ.
![]() .
.
Пример выполнения задачи 23
Условие. В
итоге проверки получено эмпирическое
распределение. Случайная величина
![]() принимает значения 0, 1, 2, 3 и 4 с
соответствующими частотами
принимает значения 0, 1, 2, 3 и 4 с
соответствующими частотами![]() .
Требуется при уровне значимости
.
Требуется при уровне значимости![]() проверить по критерию
проверить по критерию![]() гипотезу о том, что случайная величина
гипотезу о том, что случайная величина![]() распределена по закону Пуассона.
распределена по закону Пуассона.
Решение.
Критерий
![]() определяется по формуле
определяется по формуле
![]() ,
,
где
![]() ,
,![]() ,
а в качестве параметра
,
а в качестве параметра![]() возьмем выборочное среднее.
возьмем выборочное среднее.
Получим:
![]() ,
, .
.
Находим значения
![]() :
:
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
Полученные результаты занесем в таблицу
|
|
0 |
1 |
2 |
3 |
4 |
|
|
137 |
100 |
45 |
15 |
4 |
|
|
128,304 |
107,811 |
45,114 |
12,771 |
2,673 |
Вычислим
![]() .
.
Найдем
![]() ,
используя системуMathCAD,
где
,
используя системуMathCAD,
где
![]() – число степеней свободы, определяемое
по формуле:
– число степеней свободы, определяемое
по формуле:![]() .
.
![]() –число вариант;
–число вариант;
![]() – число параметров, рассчитанных по
выборке.
– число параметров, рассчитанных по
выборке.
Получим:
![]() .
.
Тогда
![]() .
.
Сравним
![]() и
и![]() .
Т.к. 2,203 < 11,345, то
.
Т.к. 2,203 < 11,345, то![]() <
<![]() ,
и, следовательно, нет оснований отвергать
гипотезу о том, что случайная величина
,
и, следовательно, нет оснований отвергать
гипотезу о том, что случайная величина![]() распределена по закону Пуассона.
распределена по закону Пуассона.
Ответ. Гипотезу принимаем.
