Задания для самостоятельной работы студентов

Задача № 1

1. Из города А в город В ведут пять дорог, а из города В в город С – три дороги. Сколько путей, проходящих через В, ведут из А в С?

2. Имеется пять видов конвертов без марок и четыре вида марок одного достоинства. Сколькими способами можно выбрать конверт с маркой для посылки письма?

3. Сколькими способами можно выбрать на шахматной доске белый и черный квадраты, не лежащие на одной и той же горизонтали и вертикали?

4. Из 12 слов мужского рода, 9 женского и 10 среднего надо выбрать по одному слову каждого рода. Сколькими способами может быть сделан этот выбор?

5. Имеется 6 пар перчаток различных размеров. Сколькими способами можно выбрать из них одну перчатку на левую руку и одну – на правую руку так, чтобы эти перчатки были различных размеров?

6. Сколько словарей нужно издать, чтобы можно было непосредственно выполнять переводы с любого из пяти языков: русского, английского, французского, немецкого, итальянского, на любой другой из этих пяти языков?

7. В урне лежат жетоны с числами 1, 2, 3, …, 10. из нее вынимают 3 жетона. Во скольких случаях сумма написанных на них чисел не меньше 9?

8. У англичан принято давать детям несколько имен. Сколькими способами можно назвать ребенка, если общее число имен равно 300, а ему дают не более трех имен?

9. Пять девушек и трое юношей играют в городки. Сколькими способами они могут разбиться на две команды по 4 человека в каждой команде, если в каждой команде должно быть хотя бы по одному юноше?

10. Надо послать 6 срочных писем. Сколькими способами это можно сделать, если для передачи писем можно послать трех курьеров и каждое письмо можно дать любому из курьеров?

11. У одного человека есть 7 книг по математике, а у другого – 9 книг. Сколькими способами они могут обменять книгу одного на книгу другого?

12. На собрании должны выступить 5 человек: А, Б, В, Г и Д. сколькими способами можно расположить их в списке ораторов при условии, что Б не должен выступать до того, как выступит А?

13. Сколькими способами можно посадить за круглый стол 5 мужчин и 5 женщин так, чтобы никакие два лица одного пола не сидели рядом?

14. Из колоды, содержащей 52 карты, вынули 10 карт. Во скольких случаях среди этих карт окажется не менее двух тузов?

15. В местком избрано 9 человек. Из них надо выбрать председателя, заместителя председателя, секретаря и культорга. Сколькими способами это можно сделать?

16. Автомобильные номера состоят из одной, двух или трех букв и четырех цифр. Найти число таких номеров, если используются 28 букв русского алфавита.

17. Сколькими способами можно расставить белые фигуры (2 коня, 2 слона, 2 ладьи, ферзя и короля) на первой линии шахматной доски?

18. В почтовом отделении продаются открытки 10 сортов. Сколькими способами можно купить в нем 8 открыток?

19. Четверо студентов сдают экзамен. Сколькими способами могут быть поставлены им отметки, если известно, что никто из них не получил неудовлетворительной отметки?

20. Рота состоит из 3 офицеров, 6 сержантов и 60 рядовых. Сколькими способами можно выделить из них отряд, состоящий из одного офицера, двух сержантов и 20 рядовых?

21. На школьном вечере присутствуют 12 девушек и 15 юношей. Сколькими способами можно выбрать из них 4 пары для танца?

22. Сколькими способами можно надеть 5 различных колец на пальцы одной руки, исключая большой палец?

23. Сколькими способами можно составить 6 слов из 32 букв, если в совокупности этих 6 слов каждая буква используется только один раз?

24. Сколько различных браслетов можно сделать из пяти одинаковых изумрудов, шести одинаковых рубинов и семи одинаковых сапфиров (в браслет входят все 18 камней)?

25. В урне лежат жетоны с числами 1, 2, 3, …, 10. из нее вынимают 3 жетона. Во скольких случаях сумма написанных на них чисел равна 9?

26. Сколькими способами можно выбрать из полной колоды, содержащей 52 карты, 6 карт так, чтобы среди них были все четыре масти?

27. Сколько имеется шестизначных чисел, у которых три цифры четные, а три – нечетные?

28. Сколькими способами можно разложить 9 книг на 4 бандероли по 2 книги и 1 бандероль в 1 книгу?

29. Сколькими способами можно составить трехцветный полосатый флаг, если имеется материал 5 различных цветов?

30. Из группы, состоящей из 7 мужчин и 4 женщин, надо выбрать 6 человек так, чтобы среди них было не менее 2 женщин. Сколькими способами это можно сделать?

Задача № 2

Варианты 1 – 8. Бросают две игральные кости. Определить вероятность того, что

2.1. сумма числа выпавших очков равна 7 или 9.

2.2. сумма числа очков больше 5.

2.3. разность числа выпавших очков не меньше 2.

2.4. произведение числа выпавших очков не больше 8.

2.5. сумма числа выпавших очков больше 5, но меньше 10.

2.6. сумма числа выпавших очков больше 8, а разность меньше 4.

2.7. разность числа выпавших очков меньше 4, а произведение больше 6.

2.8. сумма числа выпавших очков больше 6, а частное от деления большего числа на меньшее является целым числом.

Варианты 9 – 16. Имеются изделия четырех сортов, причем число изделий i-го сорта равно ,i=1, 2, 3, 4. Для контроля наудачу берутся изделий. Определить вероятность того, что среди нихпервосортных,,ивторого, третьего и четвертого сорта соответственно ().

2.9.

2.10.

2.11.

2.12.

2.13.

2.14.

2.15.

2.16.

Варианты 17 – 23. В лифт k-этажного дома сели n пассажиров (n<k). Каждый независимо от других с одинаковой вероятностью может выйти на любом (начиная со второго) этаже. Определить вероятность того, что все вышли на разных этажах.

2.17. k=6, n=4. 2.18. k=8, n=5. 2.19. k=10, n=6. 2.20. k=11, n=4.

2.21. k=12, n=4. 2.22. k=7, n=3. 2.23. k=13, n=3.

Варианты 24 – 30. Среди n лотерейных билетов k выигрышных. Наудачу взяли m билетов. Определить вероятность того, что среди них l выигрышных.

2.24. n=10, k=6, m=4, l=2. 2.25. n=11, k=7, m=5, l=2.

2.26. n=12, k=5, m=8, l=3. 2.27. n=9, k=6, m=4, l=2.

2.28. n=8, k=5, m=4, l=2. 2.29. n=10, k=5, m=6, l=4.

2.30. n=9, k=6, m=3, l=2.

Задача № 3

Две точки независимо друг от друга наудачу выбираются на отрезке [0;1]. Найти вероятность того, что

3.1. координата первой точки меньше удвоенной координаты второй точки.

3.2. разность координат двух точек больше 0,5.

3.3. сумма координаты первой точки и удвоенной координаты второй меньше 1,5.

3.4. частное от деления координаты первой точки на координату второй больше 0,5.

3.5. разность координат двух точек меньше 1/3.

3.6. частное от деления координаты второй точки на квадрат разности координаты первой точки и 0,25 больше 1.

3.7. произведение координат точек больше 0,25.

3.8. сумма координат точек в 5 раз меньше произведения координат.

3.9. утроенное произведение координат точек меньше суммы квадратов координат этих точек.

3.10. разность между квадратом координаты первой точки и квадратом координаты второй больше 0,25.

3.11. частное от деления координаты первой точки на куб разности координаты второй точки и 0,5 больше 1.

3.12. разность координат двух точек больше 1/4.

3.13. частное от деления координаты первой точки на квадрат разности координаты второй точки и 0,5 больше 0,5.

3.14. произведение координат точек меньше 0,25.

3.15. сумма координат точек в 5 раз больше произведения координат.

3.16. утроенное произведение координат точек больше суммы квадратов координат этих точек.

3.17. частное от деления координаты второй точки на куб разности координаты первой точки и 0,25 больше 1.

3.18. разность между квадратом координаты второй точки и квадратом координаты первой больше 0,25.

3.19. сумма координаты первой точки и удвоенной координаты второй больше 1,5.

3.20. частное от деления координаты второй точки на квадрат разности координаты первой точки и 0,25 меньше 1.

3.21. разность между квадратом координаты первой точки и квадратом координаты второй меньше 0,25.

3.22. частное от деления координаты первой точки на квадрат разности координаты второй точки и 0,5 меньше 1,5.

3.23. сумма координат двух точек больше суммы квадратов координат этих точек.

3.24. частное от деления координаты первой точки на куб разности координаты второй точки и 0,5 меньше 0,75.

3.25. разность между квадратом координаты второй точки и квадратом координаты первой меньше 0,25.

3.26. сумма координат точек больше 0,5 и меньше 1.

3.27. сумма координат двух точек меньше суммы квадратов координат этих точек.

3.28. разность координат двух точек меньше удвоенной координаты первой точки.

3.29. координата второй точки меньше удвоенной разности координаты первой точки и 0,25.

3.30. координата одной точки более чем в двое меньше координаты другой точки.

Задача № 4

Варианты 1 – 16. В двух партиях и% доброкачественных изделий соответственно. Наудачу выбирают по одному изделию из каждой партии. Какова вероятность обнаружить среди них только одно доброкачественное.

4.1. 4.2.4.3.

4.4. 4.5.4.6.

4.7. 4.8.4.9.

4.10. 4.11.4.12.

4.13. 4.14.4.15.

4.16.

Варианты 17 – 30. Вероятность того, что цель поражена при одном выстреле первым стрелком , вторым –. Первый сделал, второй –выстрелов. Определить вероятность того, что цель не поражена.

4.17. 4.18.

4.19. 4.20.

4.21. 4.22.

4.23. 4.24.

4.25.4.26.

4.27. 4.28.

4.29. 4.30.

Задача № 5

Варианты 1 – 10. Из 1000 ламп принадлежатi-й партии, i=1, 2, 3, . В первой партии 6%, во второй 5%, в третьей 4% бракованных ламп. Наудачу выбирается одна лампа.

а) Определить вероятность того, что выбранная лампа – бракованная.

б) Выбранная лампа оказалась бракованной. Найти вероятность того, что эта лампа из j-й партии.

5.1. 5.2.

5.3. 5.4.

5.5. 5.6.

5.7. 5.8.

5.9. 5.10.

Варианты 11 – 20. В первой урне белых ичерных шаров, во второйбелых ичерных. Из первой во вторую переложеношаров, затем из второй извлечен один шар.

а) Определить вероятность того, что выбранный из второй урны шар – белый.

б) Извлеченный шар оказался белым. Найти вероятность того, что во вторую урну переложили белых шаров.

5.11.

5.12.

5.13.

5.14.

5.15.

5.16.

5.17.

5.18.

5.19.

5.20.

Варианты 21 – 30. В магазин поступают однотипные изделия с трех заводов, причем i-й завод поставляет % изделий (i=1, 2, 3). Среди изделий i-го завода % первосортных. Куплено одно изделие.

а) Найти вероятность того, что купленное изделие – первосортное.

б) Купленное изделие оказалось первосортным. Определить вероятность того. Что это изделие выпущено j-м заводом.

5.21.

5.22.

5.23.

5.24.

5.25.

5.26.

5.27.

5.28.

5.29.

5.30.

Задача № 6

Вероятность выигрыша в лотерею на один билет равна . Купленобилетов. Найти наивероятнейшее число выигрышных билетов и соответствующую вероятность.

6.1. 6.2.6.3.

6.4. 6.5.6.6.

6.7. 6.8.6.9.

6.10. 6.11.6.12.

6.13. 6.14.6.15.

6.16. 6.17.6.18.

6.19. 6.20.6.21.

6.22. 6.23.6.24.

6.25. 6.26.6.27.

6.28. 6.29.6.30.

Задача № 7

Варианты 1 – 16. Вероятность поражения мишени при одном выстреле равна . Какова вероятность того, что привыстрелах стрелок поразит мишеньраз?

7.1. 7.2.

7.3. 7.4.

7.5. 7.6.

7.7. 7.8.

7.9. 7.10.

7.11. 7.12.

7.13. 7.14.

7.15. 7.16.

Варианты 17 – 31. При вытачивании гаек наблюдается в среднем % брака. Найти вероятность того, что в партии изгаек ровногаек окажутся не бракованными.

7.17. 7.18.

7.19. 7.20.

7.21. 7.22.

7.23. 7.24.

7.25. 7.26.

7.27. 7.28.

7.29. 7.30.

Задача № 8

Вероятность наступления некоторого события в каждом из независимых испытаний равна. Определить вероятность того, что числонаступлений события удовлетворяет следующему неравенству.

Варианты 1 – 10:

Варианты 11 – 20:

Варианты 21 – 30:

8.1. 8.2.

8.3. 8.4.

8.5. 8.6.

8.7. 8.8.

8.9. 8.10.

8.11. 8.12.

8.13. 8.14.

8.15. 8.16.

8.17. 8.18.

8.19. 8.20.

8.21. 8.22.

8.23. 8.24.

8.25. 8.26.

8.27. 8.28.

8.29. 8.30.

Задача № 9

Вероятность «сбоя» в работе телефонной станции при каждом вызове равна . Поступиловызовов. Определить вероятность«сбоев».

9.1. 9.2.

9.3. 9.4.

9.5. 9.6.

9.7. 9.8.

9.9. 9.10.

9.11. 9.12.

9.13. 9.14.

9.15. 9.16.

9.17. 9.18.

9.19. 9.20.

9.21. 9.22.

9.23. 9.24.

9.25. 9.26.

9.27. 9.28.

9.29. 9.30.

Задача № 10

Найти функцию распределения ДСВ , математическое ожидание, дисперсию, среднее квадратическое отклонение этой случайной величины и вероятность попадания в интервал, если случайная величина задана законом распределения

10.1.

X	2	5	6	8
P	0,1	0,3	0,2	0,4

10.2.

X	23	25	27	29
P	0,2	0,1	0,3	0,4

10.3.

X	6	8	9	10
P	0,1	0,1	0,3	0,2

10.4.

X	32	35	37	40
P	0,1	0,3	0,4	0,2

10.5.

X	41	42	43	45
P	0,3	0,3	0,2	0,2

10.6.

X	11	12	13	15
P	0,2	0,5	0,2	0,1

10.7.

X	51	52	54	57
P	0,1	0,4	0,3	0,2

10.8.

X	20	21	22	26
P	0,5	0,2	0,2	0,1

10.9.

X	30	32	34	36
P	0,2	0,4	0,3	0,1

10.10.

X	48	50	51	53
P	0,3	0,2	0,2	0,3

10.11.

X	5	6	8	9
P	0,1	0,5	0,2	0,2

10.12.

X	13	15	17	19
P	0,1	0,2	0,3	0,4

10.13.

X	11	12	16	19
P	0,1	0,3	0,4	0,2

10.14.

X	22	24	27	30
P	0,3	0,1	0,3	0,3

10.15.

X	40	41	43	45
P	0,1	0,4	0,3	0,2

10.16.

X	15	17	18	19
P	0,5	0,2	0,2	0,1

10.17.

X	2	4	7	9
P	0,1	0,3	0,4	0,2

10.18.

X	20	22	23	26
P	0,1	0,2	0,2	0,5

10.19.

X	30	31	32	36
P	0,2	0,3	0,3	0,2

10.20.

X	5	8	10	13
P	0,3	0,1	0,2	0,4

10.21.

X	1	4	5	6
P	0,2	0,3	0,1	0,4

10.22.

X	13	14	15	16
P	0,2	0,2	0,3	0,3

10.23.

X	10	11	14	15
P	0,1	0,5	0,2	0,2

10.24.

X	2	4	7	8
P	0,1	0,3	0,4	0,2

10.25.

X	4	5	5	7
P	0,1	0,3	0,3	0,3

10.26.

X	11	12	16	18
P	0,2	0,5	0,2	0,1

10.27.

X	2	4	7	10
P	0,3	0,4	0,2	0,1

10.28.

X	1	2	5	6
P	0,5	0,2	0,2	0,1

10.29.

X	11	14	17	18
P	0,1	0,3	0,5	0,1

10.30.

X	10	11	12	18
P	0,4	0,3	0,2	0,1

Задача № 11

Дана плотность распределения случайной величины . Найти параметр, математическое ожидание, дисперсию, функцию распределения случайной величины, вероятность попадания в интервал.

11.1.

11.2.

11.3.

11.4.

11.5.

11.6.

11.7.

11.8.

11.9.

11.10.

11.11.

11.12.

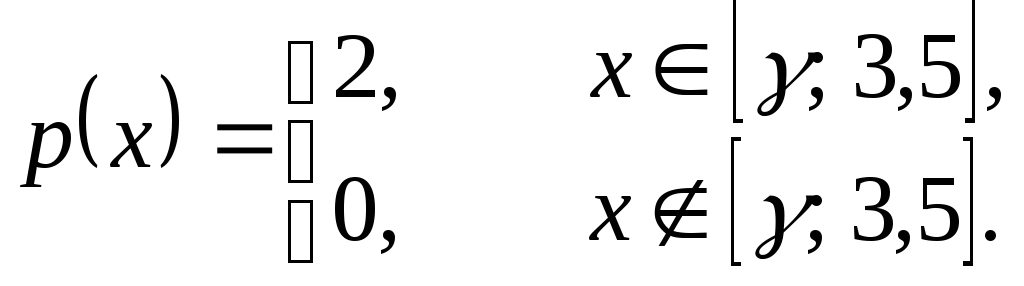
11.13.

11.14.

11.15.

11.16.

11.17.

11.18.

11.19.

11.20.

11.21.

11.22.

11.23.

11.24.

11.25.

11.26.

11.27.

11.28.

11.29.

11.30.

Задача № 12

На отрезке случайным образом выбранычисел, точнее, рассматриваютсянезависимых случайных величин, равномерно распределенных на отрезке. Найти вероятность того, что их сумма заключена междуи, т.е..

12.1.

12.2.

12.3.

12.4.

12.5.

12.6.

12.7.

12.8.

12.9.

12.10.

12.11.

12.12.

12.13.

12.14.

12.15.

12.16.

12.17.

12.18.

12.19.

12.20.

12.21.

12.22.

12.23.

12.24.

12.25.

12.26.

12.27.

12.28.

12.29.

12.30.

Задача № 13

Случайная величина имеет плотность распределения вероятностей. Найти плотность распределения вероятностейслучайной величины.

13.1. ,.

13.2. ,.

13.3. ,.

13.4. ,.

13.5. ,.

13.6. ,.

13.7. ,.

13.8. ,.

13.9. ,.

13.10. ,.

13.11. ,.

13.12. ,.

13.13. ,.

13.14. ,.

13.15. ,.

13.16. ,.

13.17. ,.

13.18. ,.

13.19. ,.

13.20. ,.

13.21. ,.

13.22. ,.

13.23. ,.

13.24. ,.

13.25. ,.

13.26. ,.

13.27. ,.

13.28. ,.

13.29. ,.

13.30. ,.

Задача №14

Задание 1. По данному графику функции плотности распределения вероятности случайной величины Х (см. рис.1.):

а) определите математическое ожидание случайной величины Х а_х, среднее квадратическое отклонение , медиануМ_е, моду М_о и вероятность попадания случайной величины Х в интервал ;

б) постройте график функции распределения случайной величины F(X).

Задание 2. По данному графику функции распределения случайной величины Х (см. рис.2.):

а) определите математическое ожидание случайной величины Х а_х, среднее квадратическое отклонение , медиануМ_е, моду М_о и вероятность попадания случайной величины Х в интервал ;

б) постройте график функции плотности распределения случайной величины f(X).

Вариант 1

,

Рис.1.

Рис.2.

Вариант 2

,

Рис.1.

Рис.2.

Вариант 3

,

Рис.1.

Рис.2.

Вариант 4

,

Рис.1.

Рис.2.

Вариант 5

,

Рис.1.

Рис.2.

Вариант 6

,

Рис.1.

Рис.2.

Вариант 7

,

Рис.1.

Рис.2.

Вариант 8

,

Рис.1.

Рис.2.

Вариант 9

,

Рис.1.

Рис.2.

Вариант 10

,

Рис.1.

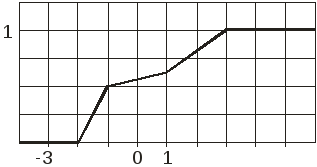
Рис.2.

Вариант 11

,

Рис.1.

Рис.2.

Вариант 12

,

Рис.1.

Рис.2.

Вариант 13

,

Рис.1.

Рис.2.

Вариант 14

,

Рис.1.

Рис.2.

Вариант 15

,

Рис.1.

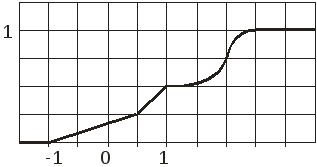
Рис.2.

Вариант 16

,

Рис.1.

Рис.2.

Вариант 13

,

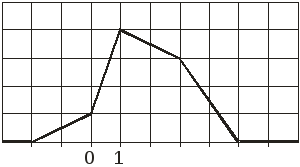
Рис.1.

Рис.2.

Вариант 18

,

Рис.1.

Рис.2.

Вариант 19

,

Рис.1.

Рис.2.

Вариант 20

,

Рис.1.

Рис.2.

Вариант 21

,

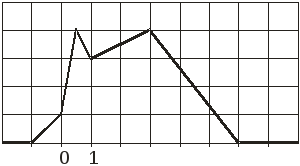
Рис.1.

Рис.2.

Вариант 22

,

Рис.1.

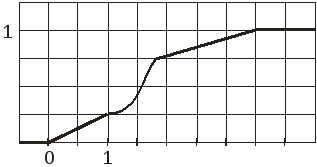
Рис.2.

Вариант 23

,

Рис.1.

Рис.2.

Вариант 24

,

Рис.1.

Рис.2.

Вариант 25

,

Рис.1.

Рис.2.

Вариант 26

,

Рис.1.

Рис.2.

Вариант 27

,

Рис.1.

Рис.2.

Вариант 28

,

Рис.1.

Рис.2.

Вариант 29

,

Рис.1.

Рис.2.

Вариант 30

,

Рис.1.

Рис.2.

Задача № 15

Варианты 1 – 15. Известно, что случайная величина имеет биномиальное распределение, неизвестным является параметр. Используя метод максимального правдоподобия, найти по реализации выборкизначение оценкинеизвестного параметра.

Варианты 16 – 30. Известно, что случайная величина имеет распределение Пуассона, неизвестным является параметр. Используя метод максимального правдоподобия, найти по реализации выборкизначение оценкинеизвестного параметра.

15.1.

15.2.

15.3.

15.4.

15.5.

15.6.

15.7.

15.8.

15.9.

15.10.

15.11.

15.12.

15.13.

15.14.

15.15.

15.16.

15.17.

15.18.

15.19.

15.20.

15.21.

15.22.

15.23.

15.24.

15.25.

15.26.

15.27.

15.28.

15.29.

15.30.

Задача № 16

Варианты 1 – 15. Известно, что случайная величина имеет распределение Пуассона, неизвестным является параметр. Используя метод моментов, найти по реализации выборкизначение оценкинеизвестного параметра.

Варианты 16 – 30. Известно, что случайная величина имеет биномиальное распределение, неизвестным является параметр. Используя метод моментов, найти по реализации выборкизначение оценкинеизвестного параметра. Условия взять из соответствующего варианта задачи №15.

Задача № 17

Случайная величина имеет нормальное распределение с неизвестным математическим ожиданиеми известной дисперсией. По выборке объемавычислено выборочное среднее. Определить доверительный интервал для неизвестного параметра распределения, отвечающий заданной доверительной вероятности.

17.1.

17.2.

17.3.

17.4.

17.5.

17.6.

17.7.

17.8.

17.9.

17.10.

17.11.

17.12.

17.13.

17.14.

17.15.

17.16.

17.17.

17.18.

17.19.

17.20.

17.21.

17.22.

17.23.

17.24.

17.25.

17.26.

17.27.

17.28.

17.29.

17.30.

Задача № 18

Случайная величина имеет нормальное распределение с неизвестными математическим ожиданием и дисперсией. По данной выборке найти доверительный интервал для математического ожидания, отвечающий доверительной вероятности.

18.1.

	21	26	31	36	41	46	51
	7	11	12	60	5	3	2

18.2.

	27	30	33	36	39	42	45
	5	15	25	40	7	5	3

18.3.

	40	45	50	55	60	65	70
	5	5	10	35	25	12	8

18.4.

	65	70	75	80	85	90	95
	3	7	10	40	20	12	8

18.5.

	20	30	40	50	60	70	80
	5	10	24	31	15	10	5

18.6.

	12	22	31	42	52	65	72
	4	16	25	40	7	5	3

18.7.

	36	42	48	54	60	66	72
	4	16	20	40	12	5	3

18.8.

	12	18	24	30	36	42	48
	2	16	12	50	15	3	2

18.9.

	7	12	17	22	27	32	37
	3	7	10	40	20	12	8

18.10.

	9	15	21	27	33	39	45
	4	10	25	30	16	10	5

18.11.

	19	16	22	28	34	40	46
	2	14	16	50	10	3	5

18.12.

	18	21	24	27	30	33	36
	4	16	10	30	15	20	5

18.13.

	8	13	18	23	28	33	38
	2	8	10	40	20	10	10

18.14.

	6	11	16	21	26	32	36
	5	25	20	30	5	9	6

18.15.

	6	10	14	18	22	26	30
	4	10	20	25	18	10	13

18.16.

	12	17	22	27	32	37	42
	15	10	14	20	14	17	10

18.17.

	16	20	24	28	32	36	40
	5	10	24	31	15	10	5

18.18.

	15	20	25	30	35	40	45
	4	6	10	35	12	25	8

18.19.

	11	15	19	23	27	31	35
	10	14	15	20	15	15	11

18.20.

	30	33	36	39	42	45	48
	15	10	20	30	14	6	5

18.21.

	6	8	12	15	20	21	25
	4	10	20	25	18	10	13

18.22.

	11	17	25	27	32	36	42
	15	11	14	20	15	11	10

18.23.

	14	18	24	28	32	36	40
	5	9	18	31	15	10	5

18.24.

	10	15	25	30	37	40	45
	4	8	10	29	12	25	8

18.25.

	8	11	19	23	27	31	35
	10	14	15	21	15	14	11

18.26.

	26	33	37	39	42	43	48
	15	16	20	31	13	6	5

18.27.

	7	10	12	18	23	26	31
	4	12	20	27	18	11	9

18.28.

	10	15	22	25	32	38	42
	12	18	19	20	14	13	10

18.29.

	12	18	24	28	34	36	40
	5	7	20	28	15	11	5

18.30.

	20	25	30	39	42	45	48
	8	10	20	31	14	6	5

Задача № 19

В результате опытов получена несмещенная оценкадля дисперсии нормальной случайной величины. Найти доверительный интервал для дисперсии при доверительной вероятности.

19.1. 19.2.

19.3. 19.4.

19.5. 19.6.

19.7. 19.8.

19.9. 19.10.

19.11. 19.12.

19.13. 19.14.

19.15. 19.16.

19.17. 19.18.

19.19. 19.20.

19.21. 19.22.

19.23. 19.24.

19.25. 19.26.

19.27. 19.28.

19.29. 19.30.

Задача № 20

По данной выборке признака найти выборочную среднюю, исправленную дисперсию и моду. Построить полигон (гистограмму) частот.

20.1.

	21	26	31	36	41	46	51
	7	11	12	60	5	3	2

20.2.

	2-5	5-8	8-11	11-14	14-17	17-20	20-23
	5	15	25	40	7	5	3

20.3.

	40	45	50	55	60	65	70
	5	5	10	35	25	12	8

20.4.

	5-10	10-15	15-20	20-25	25-30	30-35	35-40
	3	7	10	40	20	12	8

20.5.

	20	30	40	50	60	70	80
	5	10	24	31	15	10	5

20.6.

	1-5	5-9	9-13	13-17	17-21	21-25	25-29
	4	16	25	40	7	5	3

20.7.

	36	42	48	54	60	66	72
	4	16	20	40	12	5	3

20.8.

	2-5	5-8	8-11	11-14	14-17	17-20	20-23
	2	16	12	50	15	3	2

20.9.

	7	12	17	22	27	32	37
	3	7	10	40	20	12	8

20.10.

	9-15	15-21	21-27	27-33	33-39	39-45	45-51
	4	10	25	30	16	10	5

20.11.

	19	16	22	28	34	40	46
	2	14	16	50	10	3	5

20.12.

	1-8	8-15	15-22	22-29	29-36	36-43	43-50
	4	16	10	30	15	20	5

20.13.

	8	13	18	23	28	33	38
	2	8	10	40	20	10	10

20.14.

	6-9	9-12	12-15	15-18	18-21	21-24	24-27
	5	25	20	30	5	9	6

20.15.

	6	10	14	18	22	26	30
	4	10	20	25	18	10	13

20.16.

	2-4	4-6	6-8	8-10	10-12	12-14	14-16
	15	10	14	20	14	17	10

20.17.

	16	20	24	28	32	36	40
	5	10	24	31	15	10	5

20.18.

	1-5	5-9	9-13	13-17	17-21	21-25	25-29
	4	6	10	35	12	25	8

20.19.

	11	15	19	23	27	31	35
	10	14	15	20	15	15	11

20.20.

	3-10	10-17	17-24	24-31	31-38	38-45	45-52
	15	10	20	30	14	6	5

20.21.

	6	8	12	15	20	21	25
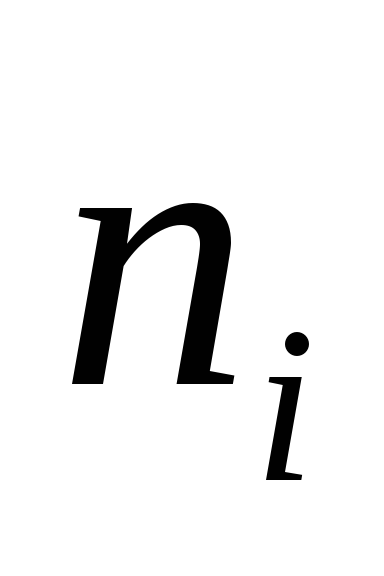
	4	10	20	25	18	10	13

20.22.

	1-4	4-7	7-10	10-13	13-16	16-19	19-22
	15	11	14	20	15	11	10

20.23.

	14	18	24	28	32	36	40
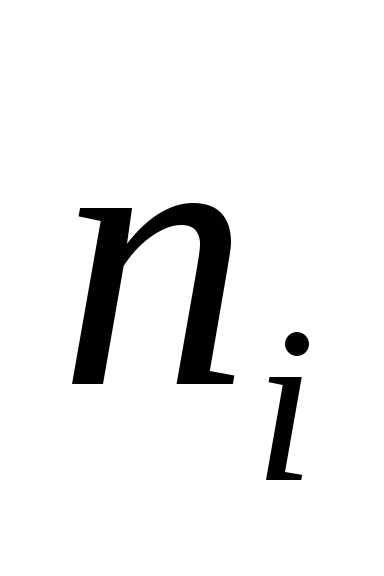
	5	9	18	31	15	10	5

20.24.

	5-7	7-9	9-11	11-13	13-15	15-17	17-19
	4	8	10	29	12	25	8

20.25.

	8	11	19	23	27	31	35
	10	14	15	21	15	14	11

20.26.

	2-6	6-10	10-14	14-18	18-22	22-26	26-30
	15	16	20	31	13	6	5

20.27.

	7	10	12	18	23	26	31
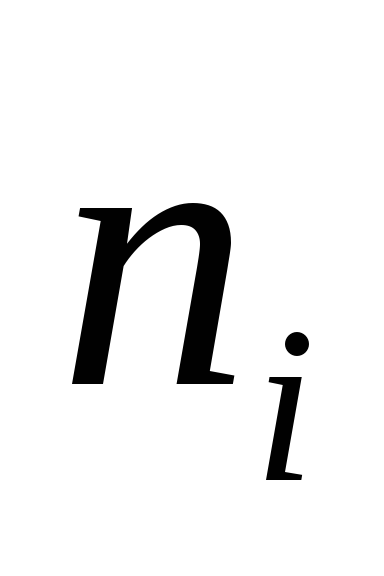
	4	12	20	27	18	11	9

20.28.

	1-6	6-11	11-16	16-21	21-26	26-31	31-36
	12	18	19	20	14	13	10

20.29.

	12	18	24	28	34	36	40
	5	7	20	28	15	11	5

20.30.

	1-4	4-7	7-10	10-13	13-16	16-19	19-22
	4	8	12	35	14	12	8

Задача № 21

На плоскости даны 6 точек, координаты которых занесены в таблицу. Пусть случайная величина – абсцисса точек, а случайная величина– ордината. Найти коэффициент линейной корреляции. Написать уравнения линейной регрессиинаина.

21.1.

	-1,1	-0,8	-0,4	0,1	0,8	1,3
	-5,7	-5,1	-4,1	-2,9	-1,4	-0,2

21.2.

	-1,2	-0,9	-0,5	0,2	0,9	1,4
	5,1	4,8	4,6	4,1	3,6	3,2

21.3.

	-1,1	-0,8	-0,4	0,1	0,8	1,3
	-1,7	-1,1	-0,4	0,5	1,7	2,6

21.4.

	1,1	2,2	2,9	3,1	3,5	3,8
	-4,7	-8,2	-10,5	-11,1	-12,4	-13,2

21.5.

	-1,2	-0,9	-0,5	0,2	0,9	1,4
	0,7	0,9	1,1	1,9	2,4	2,8

21.6.

	-2,3	-2,1	-1,9	-1,5	-0,1	0,7
	-8,7	-8,1	-7,6	-6,9	-3,4	-1,6

21.7.

	-2,1	-2,1	-1,7	-1,3	0,1	0,9
	5,7	5,1	5,4	5,1	4,1	3,6

21.8.

	-2,3	-2,1	-1,9	-1,5	-0,1	0,7
	-3,8	-3,5	-3,1	-2,4	0,4	1,6

21.9.

	-3,1	-2,9	-1,7	-0,5	0,1	0,9
	8,7	8,1	4,1	0,4	-1,5	-4,2

21.10.

	1,1	2,2	2,9	3,1	3,5	3,8
	2,6	3,5	4,1	4,2	4,4	4,7

21.11.

	0,1	0,4	0,9	1,3	1,7	2,1
	-2,7	-2,3	-1,1	-0,2	0,4	1,6

21.12.

	0,2	0,5	1,1	1,5	1,9	2,3
	4,1	3,9	3,1	3,2	2,9	2,6

21.13.

	0,1	0,4	0,9	1,3	1,7	2,1
	0,7	1,1	1,9	2,6	3,4	4,1

21.14.

	0,1	0,7	1,2	1,9	2,3	3,1
	-1,7	-3,4	-5,1	-7,3	-8,6	-11,1

21.15.

	0,2	0,5	1,1	1,5	1,9	2,3
	1,9	2,1	2,6	2,9	3,4	3,5

21.16.

	1,3	1,5	1,9	2,4	2,8	3,2
	-0,7	0,3	1,1	2,3	3,2	4,2

21.17.

	1,5	1,8	2,1	2,7	2,9	3,3
	3,2	2,9	2,7	2,3	2,4	1,9

21.18.

	1,3	1,5	1,9	2,4	2,8	3,2
	2,7	3,1	3,7	4,6	5,3	6,2

21.19.

	-1,1	-0,6	-0,1	0,1	0,9	1,1
	2,3	0,7	-0,9	-1,5	-4,4	-4,7

21.20.

	-3,1	-2,9	-1,7	-0,5	0,1	0,9
	-0,7	-0,6	0,3	1,3	1,8	2,4

21.21.

	-0,7	-0,1	0,3	0,7	1,2	1,9
	-4,8	-3,1	-2,5	-1,9	-0,4	1,2

21.22.

	-0,6	-0,1	0,5	0,7	1,4	2,1
	4,7	4,3	3,9	3,7	3,2	2,7

21.23.

	-0,7	-0,1	0,3	0,7	1,2	1,9
	-0,9	0,1	0,8	1,9	2,5	3,7

21.24.

	-3,1	-2,8	-2,1	-1,9	-0,7	0,5
	8,7	7,8	5,1	4,9	1,1	-2,8

21.25.

	1,5	1,8	2,1	2,7	2,9	3,3
	2,9	3,1	3,3	3,9	4,1	4,3

21.26.

	2,1	3,2	3,9	4,2	4,7	5,1
	1,7	4,1	5,8	6,5	7,6	8,2

21.27.

	2,3	3,1	3,7	3,9	4,1	4,8
	2,7	2,1	1,6	1,5	1,4	0,8

20.28.

	2,1	3,2	3,9	4,2	4,7	5,1
	4,1	6,1	7,1	7,9	8,8	9,5

21.29.

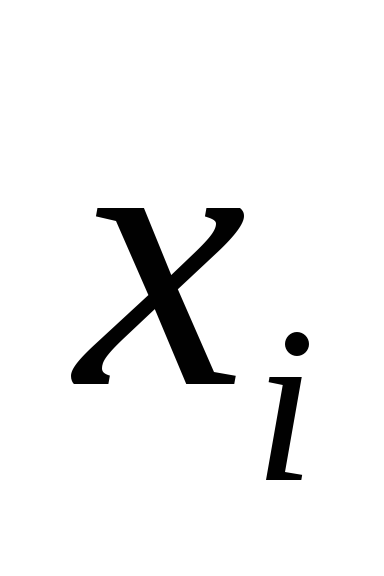
	1,2	1,9	2,3	2,7	3,2	3,8
	-5,1	-7,1	-8,6	-9,8	-11,4	-13,4

21.30.

	0,4	1,2	1,8	2,5	2,9	3,2
	-0,1	-1,1	-1,9	-2,9	-3,3	-3,7

Задача № 22.

На плоскости даны 5 точек, координаты которых занесены в таблицу. Найти функциональную зависимость , используя метод наименьших квадратов.

22.1.

	-1,5	-0,5	0	1,4	2,3
	-5,2	-2,9	-1,7	1,5	3,6

22.2.

	0	0,5	1,2	1,7	2,3
	2,1	1,8	0,1	-1,9	-5,3

22.3.

	-2	-1	0	1	2
	1,1	1,9	3,5	6,7	13,2

22.4.

	-1,1	-0,5	0,1	1,2	1,7
	1,9	0,6	0,2	1,4	2,9

22.5.

	-1,5	-0,5	0,5	1,5	2,3
	4,9	3,2	1,5	-0,3	-1,6

22.6.

	0,1	0,7	1,3	2,1	3,2
	-1,4	-0,4	2,1	7,9	20,1

22.7.

	-3	-2	-1	0	1
	-3,2	-3,3	-3,4	-3,5	-3,8

22.8.

	-1,1	-0,3	0,5	1,6	2,5
	-1,8	-0,6	0,2	0,9	1,2

22.9.

	-2,3	-1,7	-0,8	0,7	1,4
	1,5	1,9	2,5	3,6	4,1

22.10.

	0,3	0,9	1,4	1,9	2,7
	2,7	3,1	3,7	4,5	6,3

22.11.

	-2,1	-1,3	0,2	1,7	3,1
	-6,5	-4,7	-1,2	2,2	5,4

22.12.

	-0,2	0,2	0,9	1,3	1,7
	2,0	2,1	0,9	-0,3	-1,9

22.13.

	-3	-2	0	2	3
	0,7	1,1	3,5	13,2	26,1

22.14.

	0,1	1,3	2,5	2,9	3,1
	0,2	1,7	6,3	8,6	9,8

22.15.

	0,7	1,2	2,3	2,9	3,1
	1,1	0,3	-1,6	-2,6	-2,9

22.16.

	-0,5	-0,1	0,2	1,3	2,5
	-0,9	-1,4	-1,3	2,1	11,7

22.17.

	-2	-1	1	2	3
	-3,3	-3,4	-3,8	-4,4	-5,7

22.18.

	0,7	1,3	2,4	2,7	3,5
	0,4	0,8	1,2	1,2	1,1

22.19.

	0,2	1,3	1,5	2,4	3,1
	3,2	4,0	4,2	4,8	5,3

22.20.

	-0,7	0,3	1,2	2,1	2,8
	2,9	2,7	3,4	4,9	6,6

22.21.

	0,1	1,2	1,7	2,1	2,5
	-1,5	1,1	2,2	3,1	4,1

22.22.

	-4,1	-3,8	-3,2	-2,7	-2,1
	-21,4	-18,1	-12,2	-8,1	-4,1

22.23.

	-1	1	2	3	4
	1,9	6,7	13,2	26,1	51,8

22.24.

	-2,1	-1,9	-0,7	0,1	0,4
	5,7	4,7	0,9	0,2	0,3

22.25.

	-0,4	0,1	1,7	2,3	2,7
	2,9	2,1	-0,6	-1,6	-2,3

22.26.

	-2,1	-1,7	-1,2	-0,4	1,3
	7,9	4,7	1,6	-1,1	2,1

22.27.

	-1	0	1	3	4
	-3,4	-3,5	-3,8	-5,7	-8,2

22.28.

	-2,1	-1,8	-0,3	0,4	1,7
	-3,5	-2,9	-0,6	0,1	0,9

22.29.

	-3,5	-3,1	-2,4	-0,4	1,3
	0,7	0,9	1,4	2,8	4,1

22.30.

	-2,3	-1,7	-0,5	0,7	1,5
	5,8	3,9	0,3	-3,2	-6,0

Задача № 23

Варианты 1 – 15. В итоге проверки получено эмпирическое распределение. Случайная величина принимает значения в интервалах (0,1), (1,2), (2,3), (3,4) и (4,5) с соответствующими частотами. Требуется при уровне значимостипроверить по критериюгипотезу о том, что случайная величинараспределена по нормальному закону.

Варианты 16 – 30. В итоге проверки получено эмпирическое распределение. Случайная величина принимает значения 0. 1, 2, 3 и 4 с соответствующими частотами. Требуется при уровне значимостипроверить по критериюгипотезу о том, что случайная величинараспределена по закону Пуассона.

23.1.

23.2.

23.3.

23.4.

23.5.

23.6.

23.7.

23.8.

23.9.

23.10.

23.11.

23.12.

23.13.

23.14.

23.15.

23.16.

23.17.

23.18.

23.19.

23.20.

23.21.

23.22.

23.23.

23.24.

23.25.

23.26.

23.27.

23.28.

23.29.

23.30.

Задача №24

Задание №1. Найти точечные оценки ряда (выборочную среднюю, выборочную дисперсию, выборочное СКО, исправленную выборочную дисперсию, исправленное выборочное СКО, медиану, моду), построить полигон частот по выборке.

Задание №2. По имеющимся данным выполнить:

1. построить дискретный вариационный ряд;

2. построить интервальный вариационный ряд (количество интервалов равно k);

3. найти точечные оценки ряда: выборочную среднюю, выборочную дисперсию, выборочное СКО, исправленную выборочную дисперсию, исправленное выборочное СКО, медиану, моду;

4. построить гистограмму частот, полигон частот, полигон накопленных частот.

Задание №3. Смоделировать выборку объёма N, распределённую по нормальному закону с математическим ожиданием a и СКО σ. Построить гистограмму частот, полигон частот, полигон накопленных частот, сравнить с графиками плотности вероятностей и функции распределения соответственно.

Варианты

1. xi	21	26	21	36	41	46	41
   ni	7	11	12	60	5	3	2

2. ; .

3. .

1. xi	27	30	27	36	39	30	45
   ni	5	15	25	40	7	5	3

2. ; .

3. .

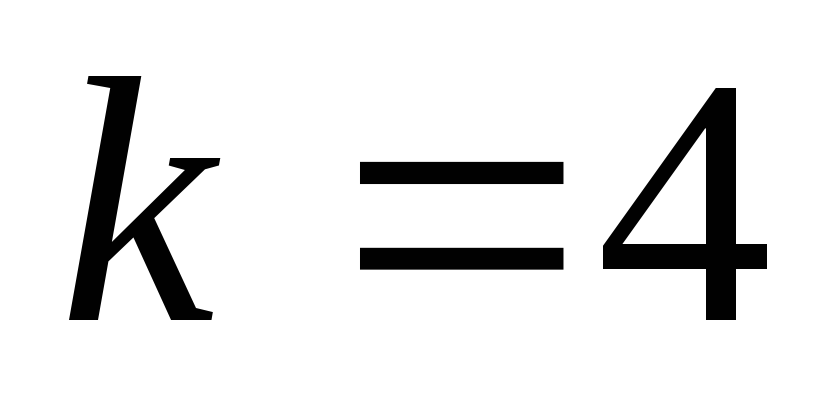1. xi	40	45	40	55	60	65	60
   ni	5	5	10	35	25	12	8

2. ; .

3. .

1. xi	65	70	75	80	65	70	95
   ni	3	7	10	40	20	12	8

2. ; .

3. .

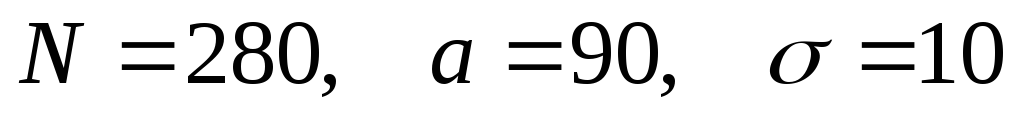1. xi	20	30	20	55	60	30	60
   ni	5	10	24	31	15	10	5

2. ; .

3. .

1. xi	12	22	12	42	52	65	22
   ni	4	16	25	40	7	5	3

2. ; .

3. .

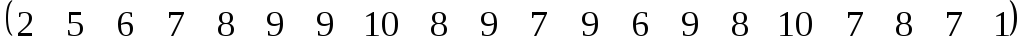1. xi	36	42	48	54	60	36	42
   ni	4	16	20	40	12	5	3

2. ; .

3. .

1. xi	12	18	24	30	36	12	24
   ni	2	16	12	50	15	3	2

2. ; .

3. .

1. xi	17	12	17	22	27	12	37
   ni	3	7	10	40	20	12	8

2. ; .

3. .

1. xi	9	15	21	27	33	21	45
   ni	4	10	25	30	16	10	5

2. ; .

3. .

1. xi	10	16	22	16	34	22	46
   ni	2	14	16	50	10	3	5

2. ; .

3. .

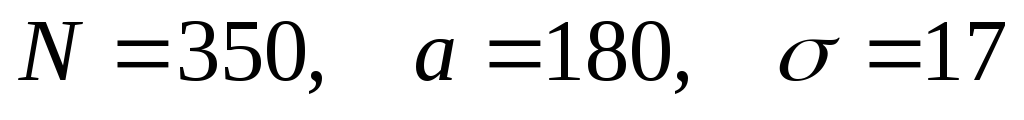1. xi	18	21	24	18	30	33	24
   ni	4	16	10	30	15	20	5

2. ; .

3. .

1. xi	18	13	18	23	28	33	28
   ni	2	8	10	40	20	10	10

2. ; .

3. .

1. xi	6	11	26	11	26	32	36
   ni	5	25	20	30	5	9	6

2. ; .

3. .

1. xi	16	10	14	18	22	14	30
   ni	4	10	20	25	18	10	13

2. ; .

3. .

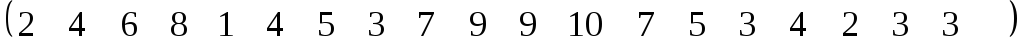1. xi	12	17	22	27	32	17	22
   ni	15	10	14	20	14	17	10

2. ; .

3. .

1. xi	36	20	24	28	32	36	20
   ni	5	10	24	31	15	10	5

2. ; .

3. .

1. xi	25	20	25	30	35	20	45
   ni	4	6	10	35	12	25	8

2. ; .

3. .

1. xi	31	35	19	23	27	31	35
   ni	10	14	15	20	15	15	11

2. ; .

3. .

1. xi	30	33	30	39	42	45	42
   ni	15	10	20	30	14	6	5

2. ; .

3. .

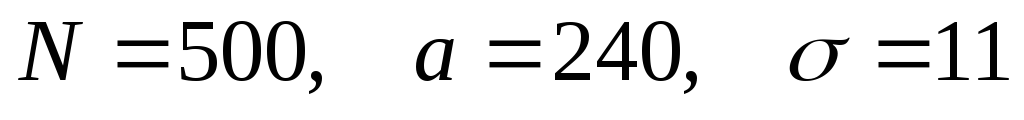1. xi	25	17	25	27	42	36	42
   ni	15	11	14	20	15	11	10

2. ; .

3. .

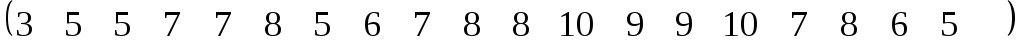1. xi	24	18	24	28	40	36	40
   ni	5	9	18	31	15	10	5

2. ; .

3. .

1. xi	10	15	25	10	37	40	25
   ni	4	8	10	29	12	25	8

2. ; .

3. .

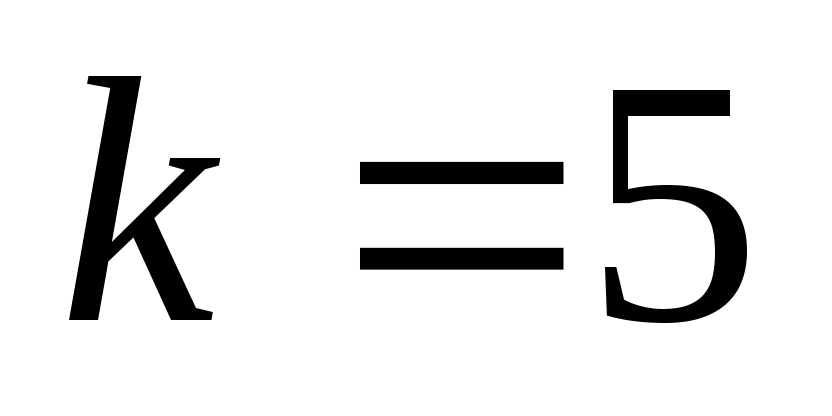1. xi	12	8	12	15	20	21	25
   ni	4	10	20	25	18	10	13

2. ; .

3. .

1. xi	8	11	19	23	27	23	35
   ni	10	14	15	21	15	14	11

2. ; .

3. .

1. xi	26	33	37	39	33	43	48
   ni	15	16	20	31	13	6	5

2. ; .

3. .

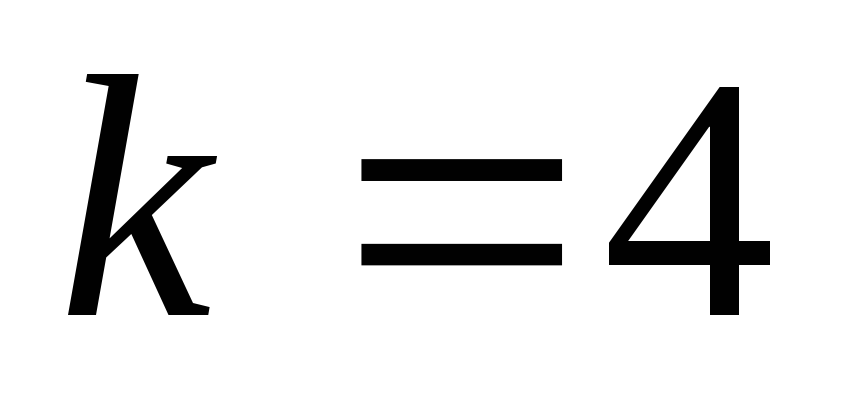1. xi	12	10	12	18	23	12	31
   ni	4	12	20	27	18	11	9

2. ; .

3. .

1. xi	10	15	22	15	32	18	15
   ni	12	18	19	20	14	13	10

2. ; .

3. .

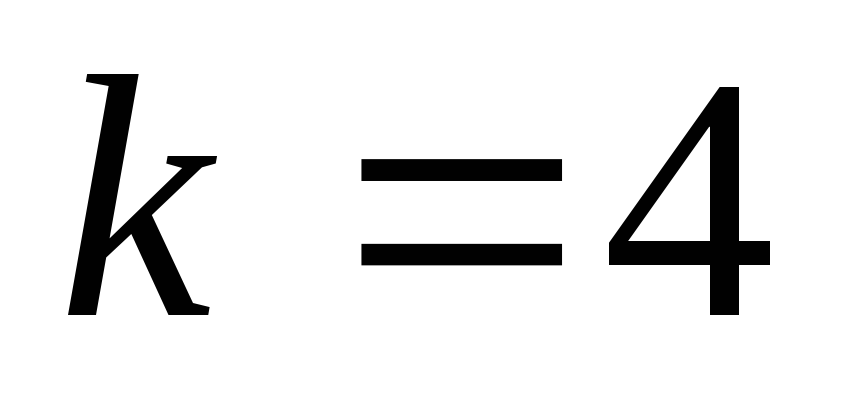1. xi	12	18	20	18	34	36	20
   ni	5	7	20	28	15	11	5

2. ; .

3. .

1. xi	11	14	19	22	14	28	19
   ni	10	13	15	20	15	16	11

2. ; .

3. .

Задача №25

Задание №1. Дана зависимость , где х и у измерены непосредственно. Известно, что . Найти и .

Задание №2. Изобразить прямоугольный треугольник и отметить на нём три параметра (две стороны и угол). Считая, что х и у доступны для измерения, выполнить косвенные измерения z. Сравнить с прямым измерением z.

25.1. .

25.2. .

25.3. .

25.4. .

25.5. .

25.6. .

25.7. .

25.8. .

25.9. .

25.10. .

25.11. .

25.12. .

25.13. .

25.14.

25.15. .

25.16. .

25.17. .

25.18. .

25.19. .

25.20. .

25.21. .

25.22.

25.23. .

25.24. .

25.25. .

25.26. .

25.27. .

25.28. .

25.29. .

25.30. .