Законы распределения случайных погрешностей

(на примере математического маятника).

Цель работы: изучить основные законы распределения случайных погрешностей.

Введение.

Измерить физическую величину абсолютно точно принципиально невозможно по следующим причинам:

а) несовершенство приборов;

б) влияние внешних условий на характеристики приборов;

в) влияние внешних факторов на параметры изучаемого объекта;

г) субъективные человеческие факторы.

Учитывая все выше изложенное, на практике возможно указать лишь диапазон значений, в который попадает истинное значение искомой величины с определенной вероятностью:

хх,

где х– абсолютная ошибка измерений.

Этот диапазон называют доверительным интервалом с соответствующей надежностью . Абсолютную ошибку измерений определяют как разницу между истинным и измеренным значением определяемой величины. Но, так как, истинное значение не известно, то существуют разные способы оценки абсолютной погрешности. Для бесконечно большого числа измерений применяют следующие способы (на практике они применяются при условииn30):

1) в качестве абсолютно погрешности х принимают среднеарифметическую погрешность:

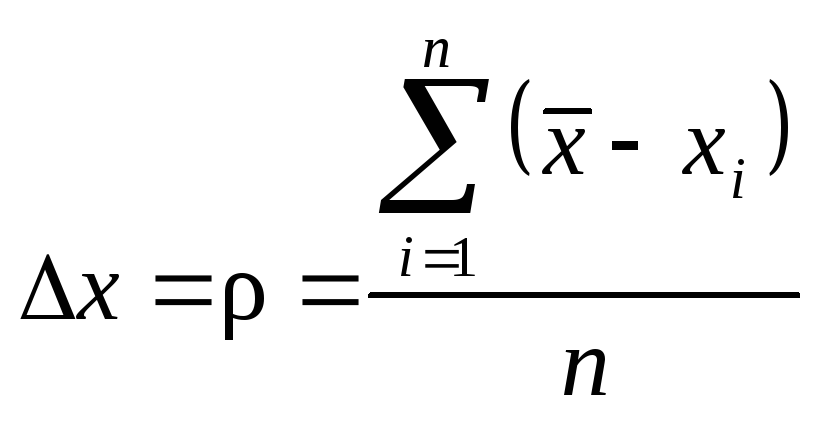с надежностью=0,57, (1)

где: – средняя величинаnизмеренных значений искомой величины,

x_i– величина каждого измерения;

2) в качестве абсолютной погрешности хпринимают среднеквадратичную погрешность:

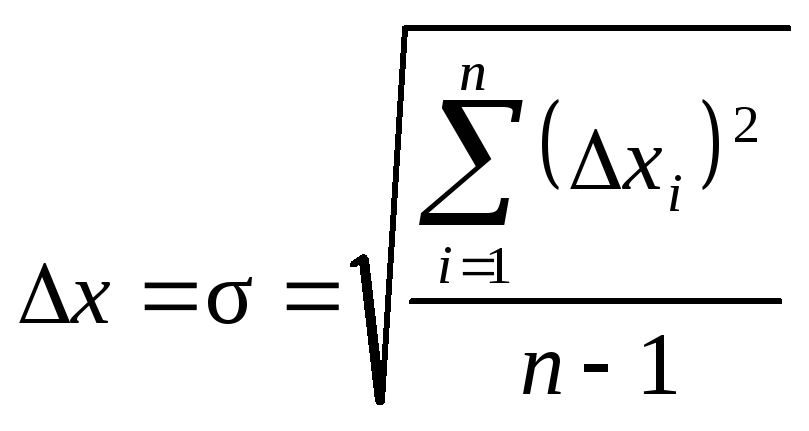, с надежностью=0,68; (2)

3) в качестве абсолютной погрешности х принимают вероятную погрешность:

х=, с надежностью=0,5.

Для нахождения вероятной погрешности все экспериментально определенные погрешностих_i, взятые по модулю, записывают в ряд по мере их возрастания и в качестве вероятной погрешности берут ошибку, приходящуюся на средину ряда.

Для ,исуществуют теоретические соотношения:

;;(3)

Все абсолютные погрешности разделяют на две большие группы:

1. Систематические погрешности. Систематическими называют погрешности, величина и знак которых не изменяются при повторении измерений.

2. Случайные погрешности. Случайными называются погрешности, величина и знак которых изменяются при повторении измерений.

Несмотря на хаотичность случайных погрешностей, их значения подчиняются определенным закономерностям. Изучить эти закономерности можно на примере математического маятника. Делается это следующим образом. По значениям периодов колебаний вычисляются абсолютные погрешности отдельно взятых измерений _i. В качестве примера в данной работе предлагается таблица значений абсолютных погрешностей (таблица 1). Для удобства анализа они систематизированы по порядку возрастания, а не так как они получались на опыте. Для изучения закономерностей распределения случайных погрешностей на основании экспериментальных данных строится гистограмма.

Таблица 1

1	-0,047	7	-0,024	13	-0,009	19	0	25	0,013	31	0,027
2	-0,041	8	-0,021	14	-0,007	20	0,002	26	0,014	32	0,032
3	-0,039	9	-0,018	15	-0,006	21	0,004	27	0,017	33	0,034
4	-0,034	10	-0,016	16	-0,004	22	0,006	28	0,019	34	0,039
5	-0,032	11	-0,014	17	-0,003	23	0,009	29	0,021	35	0,041
6	-0,026	12	-0,013	18	-0,001	24	0,011	30	0,023	36	0,048
=0,025

Выбирается система координат 0,причем осьстроится как в положительном, так и в отрицательном направлении. Осьразбивается на отрезки равной длины, т.е. с одинаковым шагом. В качестве размера шага, как правило, выбирается половина разряда первой значащей цифры границы доверительного интервала рассчитанного по формуле (2). Таким образом, для данного примера шаг осиравен 0,005с (в данном примере первая значащая цифраравна 2, ее разряд равен 0,01). Осьимеет единичный отрезок равный 1. По этой оси откладывается количество значений погрешностей, которые попадают в каждый выбранный интервал на оси.

Интервалы значений по оси выбираются равными величине разряда первой значащей цифры границы доверительного интервала рассчитанного по формуле (2). Для рассматриваемого примера величина интервала будет равна 0,01. Первый интервал выбирается симметрично относительно оси. Таким образом, для данного случая первый интервал будет от –0,005 до 0,005. Из таблицы 1 следует, что в этот интервал попадает 6 значений погрешностей. Поэтому на этом шаге строится прямоугольник шириной равной выбранному интервалу и высотой в шесть единиц. В следующий интервал от 0,005 до 0,015 попадает 5 значения погрешностей, т.е. на этом интервале строится прямоугольник высотой в 5 единиц и т.д. Аналогично, строятся прямоугольники для отрицательных значений абсолютных погрешностей. Пример построенной гистограммы приведен на рис.1.

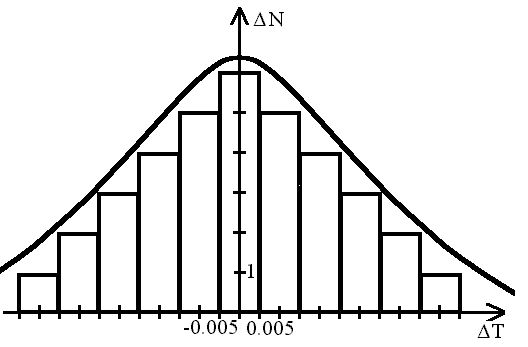
Рис.1. Гистограмма

Если шаг по оси устремить к нулю, все прямоугольники превратятся в вертикальные линии, а верхние концы этих линий сформируют плавную колоколообразную линию. После построения гистограммы на ней проводится плавная кривая, огибающая вершины прямоугольников, как показано на рисунке.

Аналитически появление случайных ошибок описывается законом нормального распределения Гаусса:

, (4)

где f(x_i) – плотность вероятности появления ошибких_i, рассчитываемая по формуле:

(5)

Если по оси Yоткладывать не значения, а выражение, то получим кривую, которая называется графиком распределения Гаусса. На рисунке 2 показаны графики распределения Гаусса с разной дисперсией.

Рис.2

Анализируя функцию распределения Гаусса и гистограмму на рисунках 1,2 можно установить основные закономерности распределения случайных погрешностей в зависимости от их величины:

1. При большом числе измерений случайные ошибки принимают непрерывный ряд значений. Это подтверждает сплошная линия на рис.1.

2. Ошибки одинаковые по величине, но разного знака встречаются одинаково часто. Из гистограммы рис.1 видно, количество ошибок в интервале от 0,005 до 0,015 на положительной ветви оси Травно количеству ошибок в таком же интервале на отрицательной ветви осиТ.

3. Частота появления ошибок уменьшается с увеличением их величины. Из гистограммы рис.1 видно, высота прямоугольников убывает вдоль оси Ткак в положительную, так и в отрицательную сторону.

Функция распределения случайных погрешностей Гаусса (6) позволяет установить физический смысл понятия «доверительная вероятность» или «надежность».

Если в соответствии с данными рис.1 доверительный интервал выберем от –0,02 до 0,02, то доверительная вероятность вычисляется путем интегрирования функции (4) в пределах выбранного интервала погрешностей:

. (6)

Тогда ответ можно будет представить в виде:

Т_ист=0,02 с надежностью=Р.

Если интервал взять «шире» от –0,05 до 0,05, то доверительная вероятность, посчитанная по формуле (6), возрастет. Это и понятно: чем шире доверительный интервал, тем вероятнее истинное значение периода колебаний попадет в этот интервал. Если интеграл (6) посчитать в пределах от –до +, то получим цифру 1. Это означает, истинное значение периода колебаний абсолютно достоверно попадет в интервал от –до +. Равенство интеграла (6) единице называется условием нормировки вероятностей.

Функция распределения Гаусса в виде, представленном формулой (4) применима на бесконечно малом интервале . В этой работе интервалынельзя считать бесконечно малыми, поэтому следует вести речь о дискретных значениях функции распределения Гаусса определенных для границ рассматриваемых интервалов.

Приравняем выражения (4) и (5):

.

Выразим и перейдем к дискретным значениям:

, (7)

где х– величина интервала,– граница интервала.

Систематические погрешности смещают гистограмму вправо или влево по оси Т,не искажая характер распределения случайных погрешностей.