4. Распределения больцмана и максвелла

Больцман нашел функцию распределения частиц (плотность вероятности заполнения частицами фазового, то есть координатно-импульсного пространства состояний) как функцию энергии

w(E) = C_*exp[-(E_k + E_p)/kT] , (5.1)

где (E_k + E_p) – суммарная кинетическая и потенциальная энергия частицы, k – постоянная Больцмана, Т – температура, а С – нормировочный множитель, легко определяемый из требования равенства единице суммы (интеграла) всех возможных вероятностей состояний частицы термодинамической системы. Если одна из энергий – кинетическая либо потенциальная – не представляет интереса для расчетов, то зависящая от нее часть экспоненциального множителя может быть просто включена в нормировочный множитель, так как кинетическая и потенциальная энергии входят в выражение (5.1) независимым образом. Поэтому максвелловское распределение молекул идеального газа по компонентам скорости для любой из декартовых координатных осей, например, х (с уже вычисленным нормировочным множителем) имеет вид

v_x) = (m/2kT)^1/2exp[- (mv_x²/2kT)], (5.2)

где через m обозначена масса отдельной частицы.

Для максвелловского распределения молекул по абсолютным значениям скоростей, используя теорему о произведении вероятностей и формулу (5.2), получаем формулу

f(v) = dN/Ndv = 4(m/2kT)^3/2exp[- (mv²/2kT)] ∙_*v ² , (5.3)

смысл которой ясен из понятия дифференциальной вероятности молекуле иметь скорость, лежащую в интервале от v до (v + dv), dP = f(v)dv, где f(v) – плотность вероятности.

Это распределение приблизительно изображено на рисунке 3.

f(v)

Рис.3. Распределение

молекул по скоростям

0

0 v <v> v_т v

Рис. 3

Из формулы (5.3) с помощью математических операций по определению средних значений величин находятся скорости:

наивероятнейшая v_н = (2kT/m)^1/2 , (5.4)

среднеарифметическая <v> = (8kT/m)^1/2 , (5.5)

тепловая (среднеквадратическая) v_т = (3kT/m)^1/2 . (5.6)

Задача 5.1

Определите среднюю потенциальную энергию молекул азота в однородном поле тяжести, считая температуру атмосферы постоянной и равной Т.

Анализ и решение

Здесь сразу предлагается для упрощения расчетов воспользоваться моделью изотермической атмосферы, что, например, для земной атмосферы довольно далеко от истины. С другой стороны, гравитационное поле Земли в наших расчетах можно действительно считать однородным, так как плотность земной атмосферы становится пренебрежимо малой уже на высоте 20 км, то есть на 1/320 земного радиуса, и это предположение довольно близко к истине. Масса молекулы азота (если понадобится) находится стандартным способом по массе одного моля делением его на число Авогадро. Больцмановское распределение (5.1) сразу дает для частиц в однородном гравитационном поле

w(E) = Cexp[-(E_p)/kT] = Cexp[-мgh/kT],

где h – высота молекулы над нулевым уровнем отсчета; g – ускорение свободного падения, которое мы считаем неизменным на всех значимых для вычислений высотах в силу быстрого убывания плотности атмосферы.

Среднее значение энергии находят стандартным в статистической физике образом через плотность вероятности интегрированием по всему интервалу значений энергии

а постоянную нормировки находят из равенства единице интеграла от плотности вероятности

С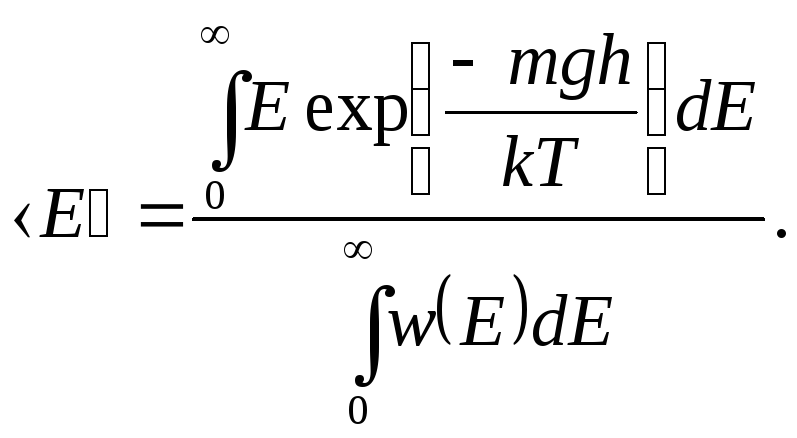ледовательно, остается вычислить интегралы в выражении

Подставляя сюда выражение зависимости потенциальной энергии молекулы от высоты, имеем

Сделав замену x = mgh/kT, получаем

что после вычисления интеграла дает <E> = kT.

Как мы видим, результат оказался независящим от массы молекул, то есть от природы молекул газа, образующего атмосферу.

Задача 5.2 Определите среднюю тепловую энергию гармонического осциллятора при температуре Т.

Анализ и решение

Поскольку в гармоническом осцилляторе полная энергия распределяется поровну между потенциальной и кинетической, то для вычисления средней энергии осциллятора достаточно вычислить одну из энергий - потенциальную либо кинетическую, а затем удвоить.

По формуле (5.1) для потенциальной энергии Е_р = ax²/2, где а – коэффициент жесткости, получаем

Здесь уже произведена нормировка. Замена переменных b = a/2kT дает

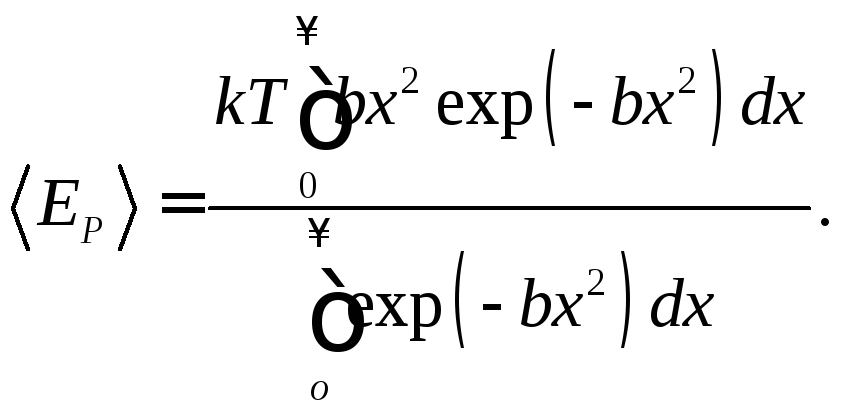
Здесь в знаменателе стоит ½ интеграла Пуассона I, равного (b)^1/2, а интеграл в числителе вычисляется дифференцированием ½ интеграла Пуассона по параметру b, когда частная производная дает

Следовательно, средняя потенциальная энергия гармонического осциллятора

<E_p> = kT/2 = <E_k>,

а полная средняя энергия классического осциллятора, равная сумме средних энергий потенциальной и кинетической, получается равной

<E> = <E_p> + <E_k> = kT.

Вывод: Хотя на каждую степень свободы поступательного или вращательного движения приходится в среднем kT/2 энергии (согласно закону равнораспределения кинетической энергии по степеням свободы), на каждую колебательную степень свободы приходится в среднем энергия, равная kT.

Задача 5.3

Считая земную атмосферу адиабатной (воздух плохой проводник тепла), покажите, что температура воздуха должна практически линейно убывать с высотой, и найдите коэффициент пропорциональности (температурный градиент земной атмосферы).

Анализ и решение

Для адиабаты связь температуры с давлением известна (смотрите решение задачи 1.3) и выражается формулой

Формула Больцмана для распределения частиц в однородном гравитационном поле (смотрите задачу 5.1) дает для отношения числа частиц и, соответственно, давлений на разных высотах (в силу уравнения P = nkT и предположительно малого изменения температуры с высотой) зависимость

где через Р₀ обозначено давление на высоте, принимаемой за нулевую (обычно таковым считают давление на уровне океана), остальные обозначения общепринятые.

Подставляя это выражение в предыдущую формулу, получаем зависимость температуры от высоты

Дифференцирование полученного выражения по высоте h дает для градиента температуры

Итак, температурный градиент земной атмосферы (быстрота понижения температуры по мере увеличения высоты) в рамках использованной модели оказался постоянным

Если теперь подставить в эту формулу реальные численные значения, то получается, что при подъеме в гору на каждый километр высоты температура будет понижаться примерно на 10К.

Необходимо помнить, что адиабатная модель атмосферы представляет собой достаточно грубое приближение, не учитывающее, например, влияние ветра или конденсации водяных паров, что, конечно, вносит существенные изменения в реальные атмосферные процессы по сравнению с полученными результатами.

Дополнительные вопросы

1. Как определяется число степеней свободы тела (молекулы)? Приведите примеры.

2. Каковы характерные скорости молекул газа при тепловом равновесии? Зависят ли эти скорости от присутствия внешнего потенциального силового поля?

3. Какое количество энергии приходится на одну степень свободы по «закону равнораспределения кинетической энергии по степеням свободы». Всегда ли этот закон выполняется? Что такое «замороженные» степени свободы?

4. Попытайтесь вычислить дисперсию скорости в максвелловском распределении, то есть квадрат среднеквадратического отклонения скорости от ее среднего значения? От какого термодинамического параметра дисперсия оказывается зависящей, и по какому закону?

5. ПРОЦЕССЫ ПЕРЕНОСА

Проникновение молекул одного вещества между молекулами другого, то естьперенос в пространстве вещества благодаря неустранимому тепловому движению молекул, называется диффузией, и макроскопически-описательно он выражается законом Фика, который для одномерного случая (диффузия вдоль оси х) принимает вид

(6.1)

где j – плотность потока вещества, измеряемая массой, переносимой в единицу времени через единичную площадку, n – концентрация вещества, D – коэффициент диффузии, а dn/dx – градиент концентрации. Знак минус означает, что вещество диффундирует в сторону уменьшения концентрации.

Перенос импульса в потоке жидкости или газа в перпендикулярном к скорости потока направлении вызывает силы внутреннего трения (силы вязкости) и называется вязкостью. Вязкость описывается законом Ньютона (одномерный случай)

( 6.2)

где F – сила вязкого трения, S – площадь, через которую передается импульс, dv_y/dx – градиент скорости потока,  коэффициент вязкости (динамическая вязкость).

Перенос энергии, осуществляющийся через вещество при отсутствии движения вещества на макроскопическом уровне (нет конвекции – «ветра») и без учета излучения называется теплопроводностью и описывается законом Фурье (одномерный случай)

(6.3)

где q – плотность потока энергии, - коэффициент теплопроводности, dT/dx – градиент температуры. Знак минус означает, что энергия (теплота) передается от более горячего участка вещества к участку с меньшей температурой.

Рассмотрение явлений переноса в газах на микроскопическом уровне, то есть с точки зрения молекулярно-кинетической теории, позволяет связать коэффициенты в уравнениях (6.1), (6.2) и (6.3) с характерными для микровзаимодействий величинами (разумеется, в рамках принятой модели упругих столкновений молекул газа), а именно (с точностью до численного множителя порядка единицы)

D = <v><l>; (6.4)

<v><l>  

<v><l>c_v  

где <v> - средняя скорость молекул, <l> - средняя длина свободного пробега молекул, плотность газа, c_v – удельная теплоемкость газа при постоянном объеме.

Из теории известна зависимость среднего числа столкновений молекулы газа в единицу времени <z> (с точностью до численного множителя порядка единицы) от скорости, концентрации и размера молекулы

<z> = <v>n_эф , (6.7)

где n – концентрация молекул газа, _эф = d² – эффективное сечение рассеяния молекулы (d называется газокинетическим диаметром молекулы).

Поскольку среднее время между столкновениями обратно <z>, то есть <t> = 1/<z>, то очевидно, что средняя длина свободного пробега

<l> = <v><t> = 1/n_эф . (6.8)

Задача 6.1

Определите газокинетический диаметр молекул водорода, если известно, что у него средняя длина свободного пробега молекул <l> при нормальных условиях равна 1,3∙10^-7 м.