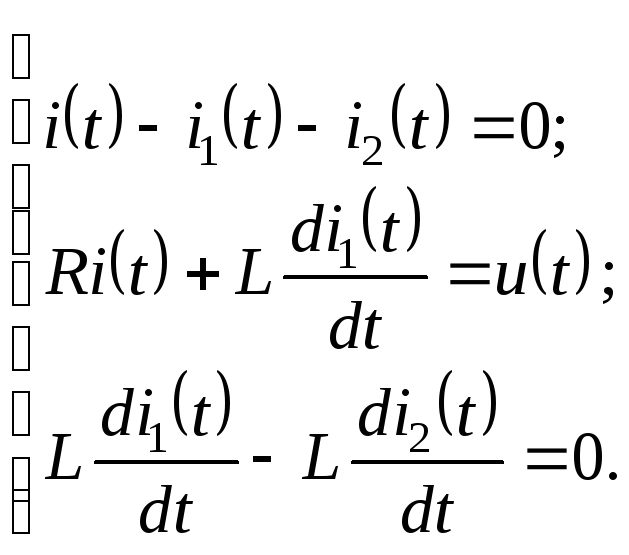- •Министерство образования и науки Российской Федерации
- •Введение
- •Перечень условных обозначений
- •1 Основные теоретические положения
- •1.1. Физические основы переходных процессов
- •1.2 Математический аппарат и алгоритмы расчетов
- •1.2.1 Классический метод анализа переходного процесса
- •1.2.2 Операторный метод расчета (метод преобразования Лапласа)
- •1.2.3 Расчет методом интеграла Дюамеля
- •1.2.4 Метод переменных состояния переходных процессов
- •2 Классический метод расчета переходных процессов в линейных электрических цепях
- •2.1 Примеры расчета переходных процессов в цепях с индуктивностью
- •Имеет один отрицательный и действительный корень
- •Решение
- •И подставим его в первое уравнение системы:
- •Источника напряжения
- •Получим характеристическое уравнение
- •Решение
- •Первый способ
- •Решение
- •Ом; Ом.
- •Решение
- •Решение
- •И падение напряжение на индуктивности
- •Решение
- •Поэтому в соответствии с первым законом Кирхгофа для узла “1” ток в индуктивности, питаемый источником тока равен току в ветви с резистором: а.
- •Откуда составляем характеристическое уравнение:
- •Где ток в конденсаторе.
- •Отсюда находим характеристическое уравнение:
- •С-1; с-1.
- •С-1; с-1.
- •Решение
- •Напряжение между узлами 1 и 2 определяется как:
- •И подставим туда ток конденсатора (2.6.6):
- •Откуда характеристическое уравнение оду будет иметь вид:
- •2.8 Задачи для самостоятельного решения
- •3 Операторный метод расчета переходных процессов в линейных электрических цепях
- •3.1 Примеры расчета переходных процессов в цепях постоянного тока
- •Решение
- •Решение
- •3.2 Примеры расчета переходных процессов в цепях переменного тока
- •С-1; с-1;
- •По закону Ома для участка цепи определяем искомый операторный ток:
- •С-1; с-1;
- •4 Расчет переходных процессов с помощью интеграла дюамеля
- •4.1 Примеры расчета переходных и импульсных характеристик
- •Тогда по закону Ома в операторной форме определяем ток
- •Решение
- •С-1; с-1;
- •4.2 Примеры расчета переходных процессов с помощью интеграла Дюамеля
- •Решение
- •4.3 Задачи для самостоятельного решения
- •5 Расчет переходных процессов методом переменных состояния
- •5.1 Примеры расчета
- •Определим собственные значения матрицы a, т.Е. Корни уравнения
- •. Определим собственные значения матрицы a, т.Е. Корни уравнения
- •5.2 Задачи для самостоятельного решения
- •Список литературы
- •Содержание
- •Часть II
- •190008, Г.С.-Петербург, ул. Лоцманская, 3.
Напряжение между узлами 1 и 2 определяется как:
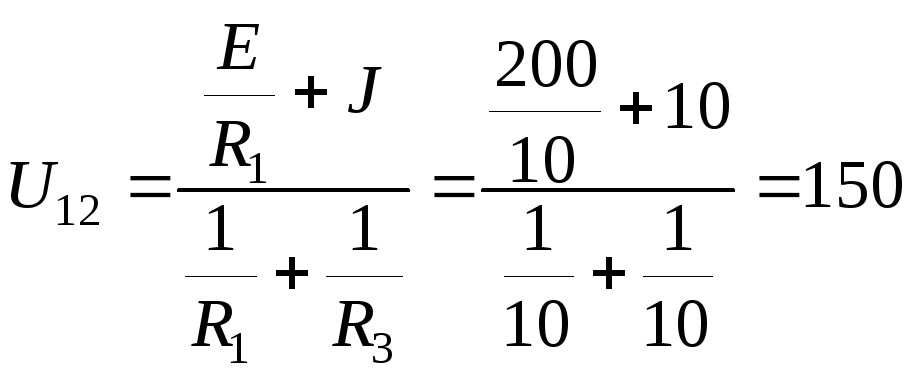 В.
В.
Тогда используя закон Ома определяем токи в первой и третьей ветвях:
![]() А;
А;
![]() А.
А.
Напряжение на конденсаторе как и при
![]() будет равно напряжению между узлами 1
и 2 или падению напряжения в резисторе
будет равно напряжению между узлами 1
и 2 или падению напряжения в резисторе
![]()
![]() В.
В.
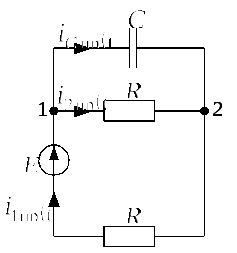
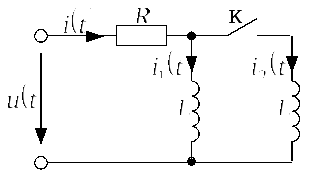
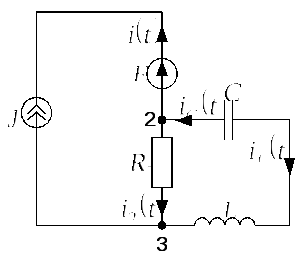
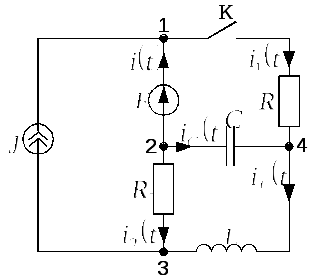
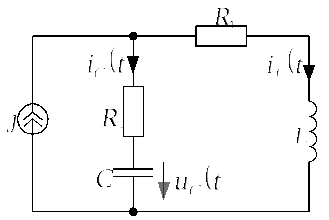
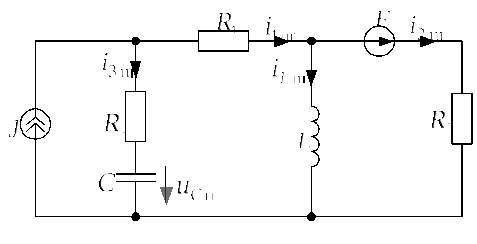
3) Для расчета переходного процесса в
момент коммутации
![]() для послекоммутационной схемы,
изображенной на рис. 2.6.2.а, составим
систему из трех уравнений: одно по
первому закону Кирхгофа для узла 1 и два
уравнения по второму закону Кирхгофа
для контуров не содержащих источник
тока, учтя, что по условию задачи
для послекоммутационной схемы,
изображенной на рис. 2.6.2.а, составим
систему из трех уравнений: одно по
первому закону Кирхгофа для узла 1 и два
уравнения по второму закону Кирхгофа
для контуров не содержащих источник
тока, учтя, что по условию задачи
![]()
|
|
(2.6.1) |
|
(2.6.2) | |
|
(2.6.3) |
где ток в конденсаторе
|
|
(2.6.4) |
Найдем из приведенной системы ток
![]() Для
этого из уравнения (2.6.2) выразим ток
Для
этого из уравнения (2.6.2) выразим ток
![]()
|
|
(2.6.5) |
Из уравнения системы (2.6.1) ток в конденсаторе определится как:
|
|
(2.6.6) |
Выразим из уравнения (2.6.3) напряжение
![]()
И подставим туда ток конденсатора (2.6.6):
![]()
После упрощений получим
|
|
(2.6.7) |
Теперь ток
![]() источника ЭДС (2.6.5) подставим в уравнение
(2.6.7):
источника ЭДС (2.6.5) подставим в уравнение
(2.6.7):
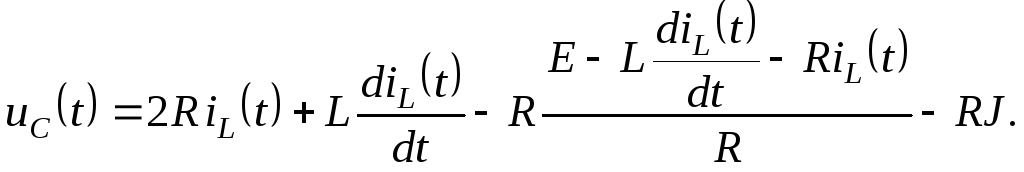
После группировки слагаемых получаем:
|
|
(2.6.8) |
Подставим (2.6.8) в уравнение (2.6.4):
|
|
(2.6.9) |
Сделаем подставку уравнений (2.6.5) и (2.6.9) в выражение (2.6.1):
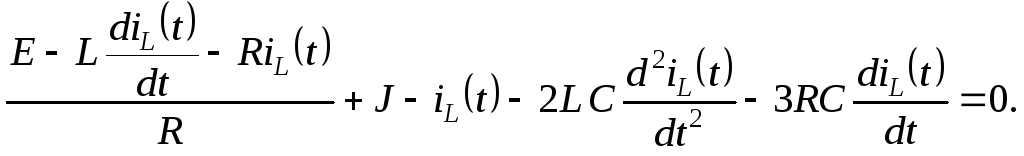
Умножив обе части последнего выражения
на
![]() и сделав группировку слагаемых, получим
НДУ, записанное относительно тока в
катушке:
и сделав группировку слагаемых, получим
НДУ, записанное относительно тока в
катушке:
|
|
(2.6.10) |
Приравняв правую часть (2.6.10) к нулю, получим ОДУ второго порядка:
![]()
Откуда характеристическое уравнение оду будет иметь вид:
![]()
![]()
![]()
Находим корни характеристического уравнения:
![]() с-1.
с-1.
Корни получаются отрицательные, одинаковые (кратные), вещественные, в силу чего общее решение НДУ (2.6.10) при двух кратных корнях имеет вид:
|
|
(2.6.11) |
Для нахождения постоянных интегрирования
![]() и
и
![]() подставим
ток в катушке (4.4.11) в выражение (4.4.8):
подставим
ток в катушке (4.4.11) в выражение (4.4.8):
![]()
или
|
|
(2.6.12) |
В итоге имеем систему уравнений (2.6.11) и (2.6.12) для определения постоянных интегрирования:
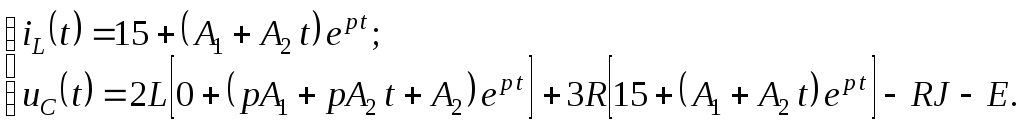
Запишем полученную систему уравнений
при
![]()
|
|
(2.6.13) |
В соответствии с первым законом коммутации ток в катушке не может измениться скачком, а по второму закону коммутации напряжение на емкости также изменяется плавно, поэтому
|
|
(2.6.14) |
|
|
(2.6.15) |
Тогда систему уравнений (2.6.13) с учетом независимых начальных условий (2.6.15) и (2.6.16) представим в виде:
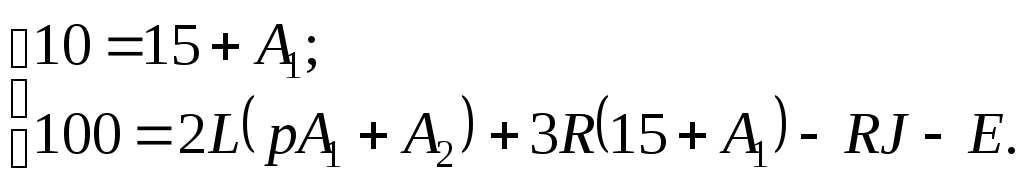
Из первого уравнения системы постоянную
интегрирования
![]() подставим во второе уравнение:
подставим во второе уравнение:
![]()
откуда
![]()
Подставив найденные постоянные интегрирования в выражение (2.6.12), найдем закон изменения тока в катушке:
![]() А.
А.
Решение НДУ второго порядка для напряжения на конденсаторе в силу кратности корней характеристического уравнения имеет вид:
|
|
(2.6.16) |
Для нахождения постоянных интегрирования
найдем ток в катушке через напряжение
![]() ,
пользуясь системой уравнений (2.6.1) –
(2.6.3).
,
пользуясь системой уравнений (2.6.1) –
(2.6.3).
Для этого вычтем почленно из уравнения (2.6.2) уравнение (2.6.3):
![]()
откуда получаем уравнение
|
|
(2.6.17) |
Выразив из уравнения (2.6.1) ток
![]() и
подставив в (2.6.17), получаем:
и
подставив в (2.6.17), получаем:
![]()
Подставим в последнее уравнение ток
![]()
![]()
откуда после упрощений находим ток
![]()
![]()
Подставим (2.6.16) в последнее уравнение:
![]()
или
|
|
(2.6.18) |
Переписав (2.6.16) и (2.6.18) получим следующую систему уравнений:

Записав эту систему при
![]() получим
получим
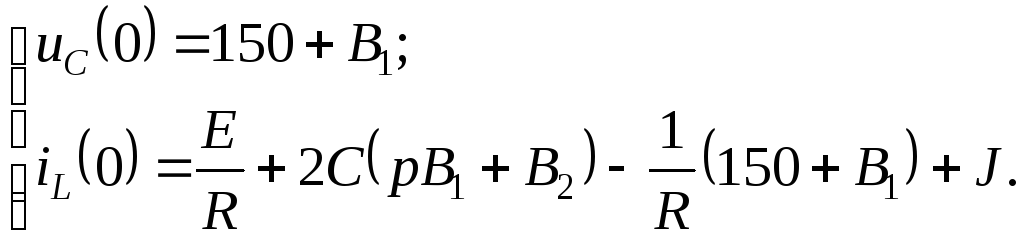
Подставив независимые начальные условия (4.4.13) и (4.4.14) в последнюю систему уравнений, получим
|
|
(2.6.19) |
Выразим из первого уравнения системы
(2.6.19) постоянную интегрирования
![]() и подставим ее во второе уравнение:
и подставим ее во второе уравнение:
![]()
откуда

Подставив найденные постоянные
интегрирования
![]() и
и
![]() в НДУ (2.6.16), получим искомое выражение
для напряжения на конденсаторе:
в НДУ (2.6.16), получим искомое выражение
для напряжения на конденсаторе:
![]() В.
В.
Рассчитаем ток в конденсаторе в соответствии с формулой (2.6.4):
![]() А.
А.
Задача 2.6.3 В цепи, изображенной на
рис. 2.6.3.а, в момент
![]() происходит замыкания ключа К. Найти ток
в индуктивности
происходит замыкания ключа К. Найти ток
в индуктивности
![]() и напряжение в конденсаторе
и напряжение в конденсаторе
![]() Параметры цепи:
Параметры цепи:![]() В,
В,
![]() А,
А,
![]() Ом,
Ом,
![]() Гн,
Гн,
![]() мкФ.
мкФ.
|
|
|
|
Рис. 2.6.3.а |
Рис.2.6.3.б |
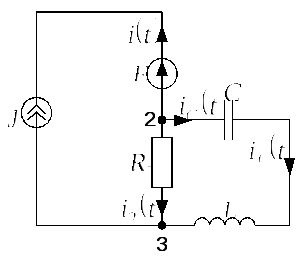
Решение
1) Цепь до коммутации
![]() изображена на рис. 2.6.3.б.
изображена на рис. 2.6.3.б.
Ток в конденсаторе
![]() равен току в индуктивности
равен току в индуктивности
![]() Заряженный конденсатор с емкостью
Заряженный конденсатор с емкостью
![]() не пропускает постоянный ток, поэтому
не пропускает постоянный ток, поэтому
![]()
Тогда на основании первого закона
Кирхгофа для узла “1” ток
![]() протекающий в ветви с последовательным
соединением резистора
протекающий в ветви с последовательным
соединением резистора
![]() и ЭДС
и ЭДС
![]() равен источнику тока
равен источнику тока
![]()
![]() А.
А.
По закону Ома найдем напряжение на
конденсаторе
![]()
![]() В.
В.
|
|
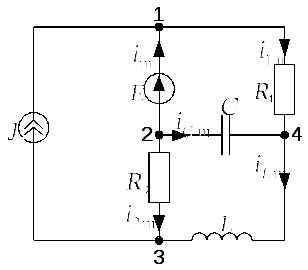
2)
Послекоммутационная схема
Составим уравнение
по второму закону Кирхгофа для контура
|
|
Рис. 2.6.3.в |
![]()
или
![]()
Подставим найденный ток
![]() в последнее уравнение:
в последнее уравнение:
![]()
Отсюда найдем принужденный ток в катушке
индуктивности
![]()
![]() А.
А.
Для нахождения напряжения в емкости
![]() составим уравнение по второму закону
Кирхгофа для контура
составим уравнение по второму закону
Кирхгофа для контура
![]()
![]()
Тогда,
![]() В.
В.
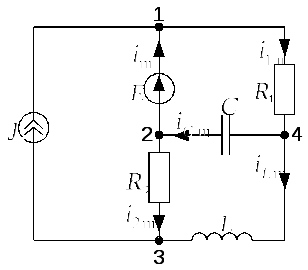
3) Для расчета переходного процесса для
схемы, приведенной на рис. 2.6.3.а, при
замыкании ключа К составим исходную
систему из четырех уравнений: первое –
по первому закону Кирхгофа для узла
“3”, второе – по первому закону Кирхгофа
для узла “4”, третье – на основании
второго закона Кирхгофа для контура
![]() четвертое – в соответствии со вторым
законом Кирхгофа для контура
четвертое – в соответствии со вторым
законом Кирхгофа для контура
![]()
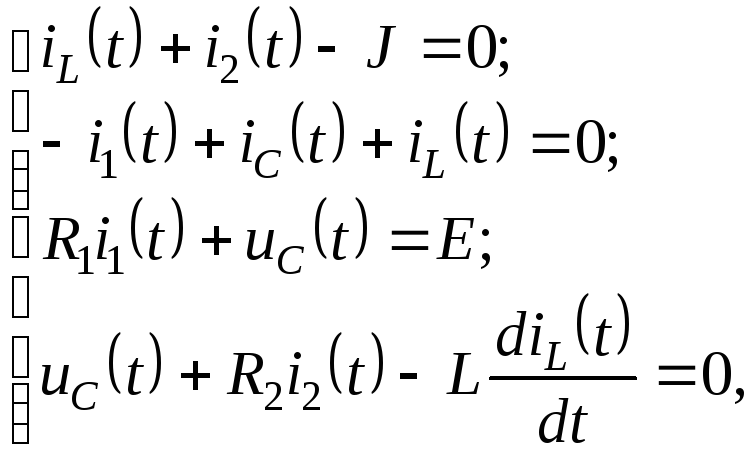
где
![]() ток
в конденсаторе,
ток
в конденсаторе,
|
|
(4.4.20) |
Решим приведенную систему уравнений
относительно напряжения
![]() следующим образом.
следующим образом.
Из третьего уравнения системы выразим
ток
![]()
![]()
Теперь подставим этот ток и ток (4.4.20) во второе уравнение исходной системы:
![]()
откуда
|
|
(2.6.21) |
Подставим (4.4.16) в первое уравнение системы:
![]()
Тогда ток в ветви с резистором
![]()
|
|
(4.4.22) |
Подставим токи (2.6.21) и (2.6.22) в четвертое уравнение исходной системы уравнений:
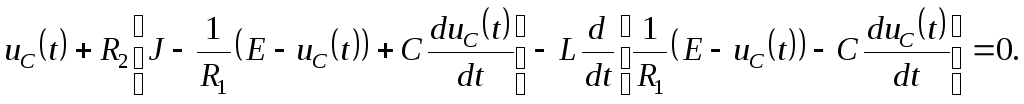
После дифференцирования по
![]() и раскрытия скобок получаем:
и раскрытия скобок получаем:
![]()
Умножив этого выражение на
![]() и сгруппировав слагаемые получим НДУ
второго порядка:
и сгруппировав слагаемые получим НДУ
второго порядка:
![]()
Приравняв правую часть записанного НДУ к нулю получим ОДУ второго порядка:
![]()
Тогда составим характеристическое уравнение:
![]()
![]()
![]()
Определим корни этого уравнения:
 с-1.
с-1.
Так как корни характеристического уравнения получились комплексно – сопряженными, то общее решение составленного выше НДУ будет иметь вид:
|
|
(2.6.23) |
Для определения постоянных интегрирования![]() и
и
![]() подставим (2.6.23) в уравнение (2.6.21):
подставим (2.6.23) в уравнение (2.6.21):
![]() ;
;
![]() .
.
Составим систему из последнего уравнения и уравнения (2.6.23):
Запишем ее при
![]()
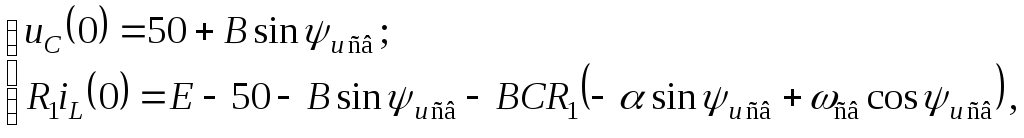
где
![]() и
и
![]() независимые
начальные условия, определяемые по
законам коммутации:
независимые
начальные условия, определяемые по
законам коммутации:
![]() В – по второму закону коммутации;
В – по второму закону коммутации;
![]() –
по первому закону коммутации.
–
по первому закону коммутации.
Тогда последняя система уравнений преобразуется к виду:
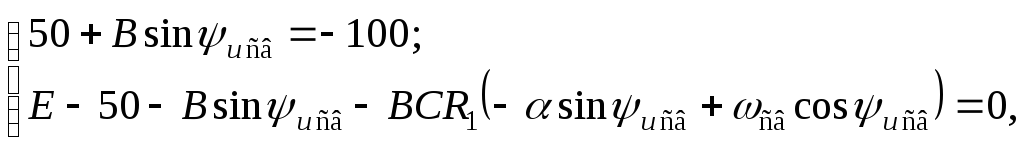
или
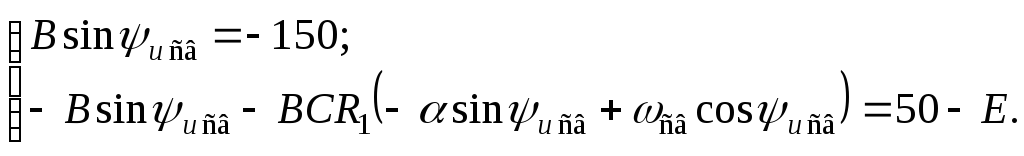
Выразив из первого уравнения последней
системы
![]() и подставив во второе, получим:
и подставив во второе, получим:
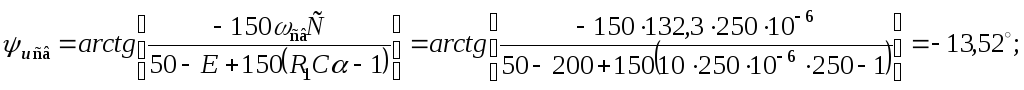
![]()
Таким образом, закон изменения напряжения на конденсаторе имеет вид:
![]() В.
В.
Запишем общее решение НДУ для тока в
катушке
![]()
|
|
(2.6.24) |
Для нахождения постоянных интегрирования
![]() и
и
![]() из исходной системы уравнений сначала
найдем напряжение
из исходной системы уравнений сначала
найдем напряжение
![]() через ток в индуктивности
через ток в индуктивности
![]() Для этого ток из первого уравнения
системы
Для этого ток из первого уравнения
системы
![]() подставим в четвертое уравнение:
подставим в четвертое уравнение:
![]()
Откуда определим напряжение на
конденсаторе
![]()
|
|
(2.6.25) |
Теперь подставим (2.6.24) в выражение (2.6.25):
![]()
![]()
Переписав (2.6.24) и последнее выражение получим следующую систему уравнений:
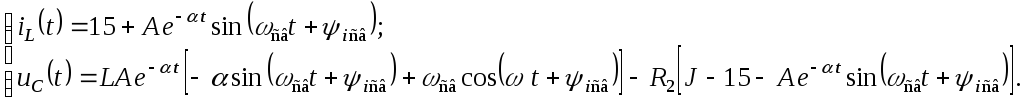
При
![]() последняя система приобретает вид:
последняя система приобретает вид:
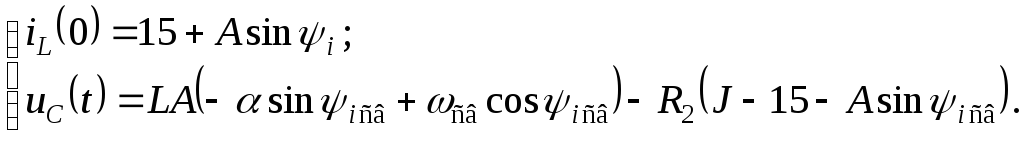
Подставив сюда приведенные выше
независимые начальные условия –
![]() и
и
![]() получим
получим
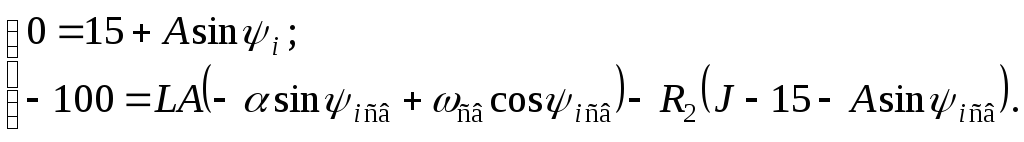
Сделав группировку слагаемых, окончательно
получим систему из двух уравнений с
двумя неизвестными
![]() и
и
![]()

Путем подстановки
![]() из первого уравнения этой системы во
второе, находим постоянные интегрирования:
из первого уравнения этой системы во
второе, находим постоянные интегрирования:
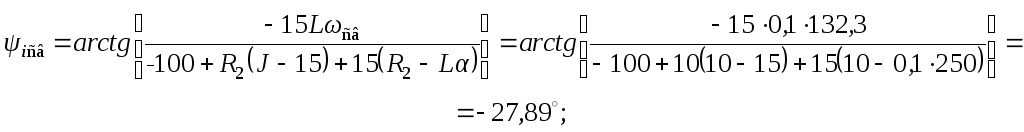
![]()
Подставив все найденные величины в
(2.6.24) окончательно получим выражение
для переходного тока в индуктивности
![]()
![]() А.
А.
Задача 2.6.4В цепи, изображенной на
рис. 2.6.4.а, в момент
![]() происходит замыкание ключа К. Определить
ток
происходит замыкание ключа К. Определить
ток
![]() и параметры цепи, если известно, что
и параметры цепи, если известно, что
![]() А,
А,
![]() Ом,
Ом,
![]() постоянные источники.
постоянные источники.
|
|
|
|
Рис. 2.6.4.а |
Рис.2.6.4.б |
Решение
По условию задачи известен закон изменения тока в катушке индуктивности, который запишем в следующем виде:
![]()
Т.е. нам известны корни характеристического
уравнения
![]() с-1.
с-1.
1) Схема в установившемся режиме приведена на рис. 2.6.4.б.
Ток в конденсаторе равен нулю:
![]()
По условию задачи известна принужденная
составляющая тока в катушке
![]() А. Поэтому
А. Поэтому
![]() А.
А.
Согласно методу двух узлов имеем:
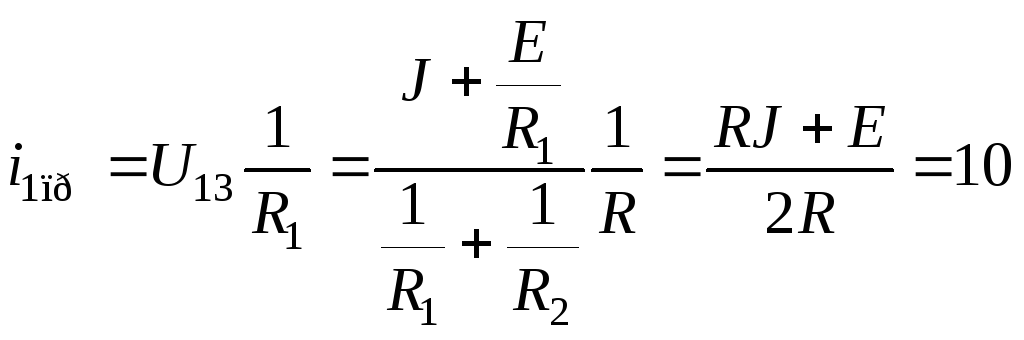 А.
А.
Тогда можно записать:
![]()
|
|
(2.6.26) |
2) Определим параметры цепи из характеристического уравнения, которое возьмем из решения задачи 2.6.3:
![]()
Так как
![]() можно записать:
можно записать:
![]()
или
![]()
По условию задачи известны корни этого уравнения:
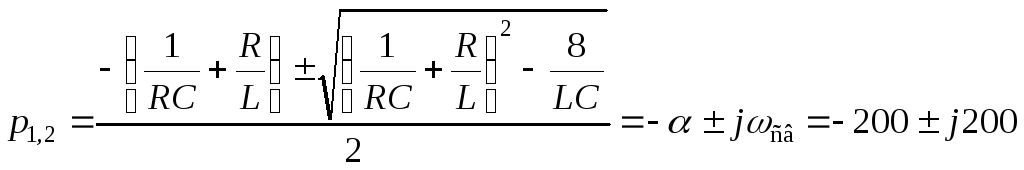 с-1.
с-1.
Тогда запишем следующие соотношения:
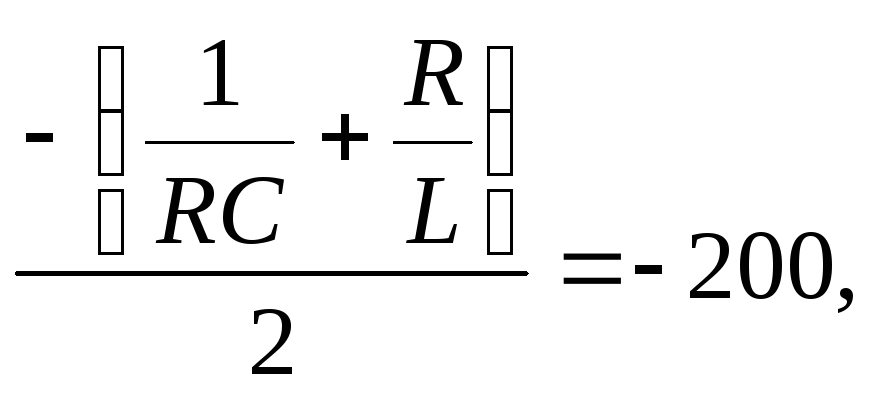
откуда
|
|
(2.6.27) |
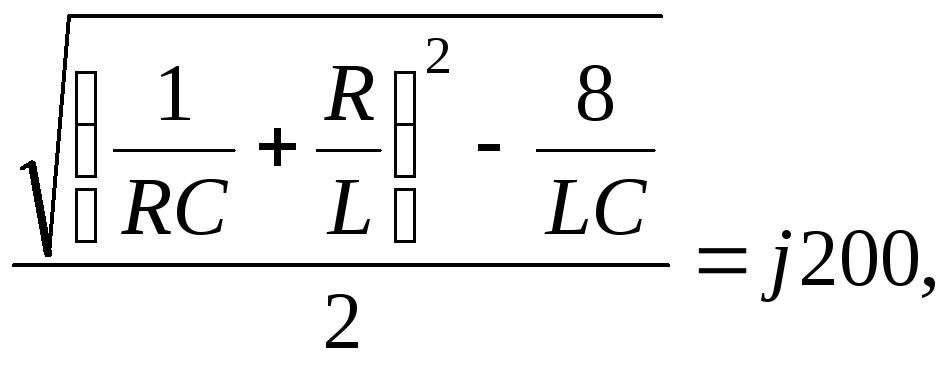
или
![]()
Подставим (2.6.27) в первое слагаемое последнего выражения:
![]()
Следовательно,
![]()
![]()
Подставим последнее соотношение в (2.6.27):
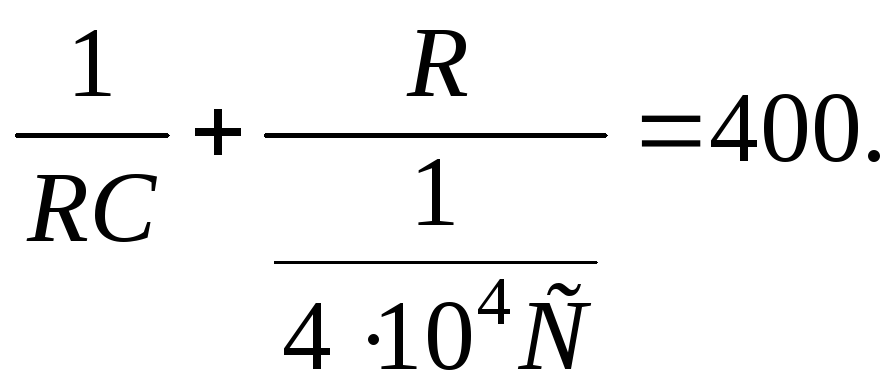
Тогда
![]()
![]()
![]()
Найдем только положительный корень, так как емкость С – величина положительная:
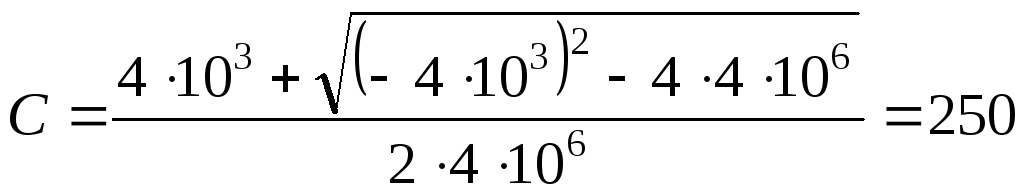 мкФ.
мкФ.
Зная емкость С, найдем индуктивность:
![]() Гн.
Гн.
|
|
3) Схема до коммутации приведена на рис. 2.6.4.в. Ток в катушке равен нулю:
Тогда напряжение на конденсаторе
4)
Расчет схемы в момент коммутации.
Переходной ток
Для
определения постоянных интегрирования
|
|
Рис. 2.6.4.в |
![]() надо знать зависимые начальные условия:
надо знать зависимые начальные условия:
![]() и
и
![]()
Для их определения составим исходную
систему из двух уравнений согласно
схеме, изображенной на рис. 2.6.4.а, при
![]()
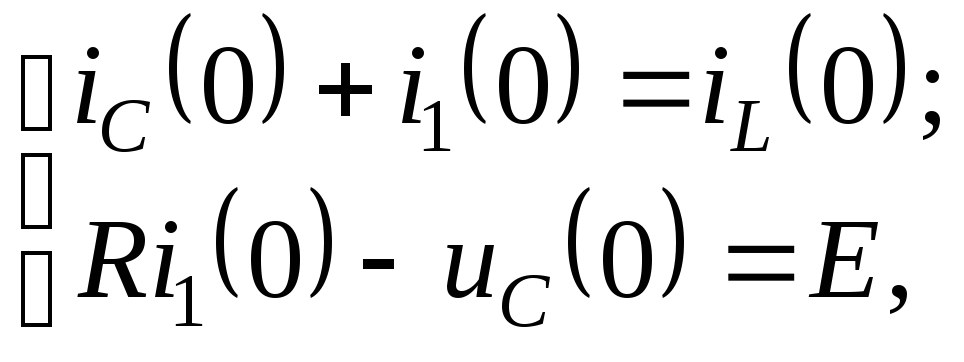
где
![]()
![]() по
второму закону коммутации.
по
второму закону коммутации.
С учетом этих замечаний перепишем данную систему следующим образом:
|
|
(2.6.29) |
Из второго уравнения системы (2.6.29) найдем
начальное значение тока
![]() учитывая полученную ранее зависимость
(2.6.26):
учитывая полученную ранее зависимость
(2.6.26):
![]() А.
А.
Тогда из первого уравнения системы (2.6.29) определим начальное значение тока в конденсаторе:
![]() А.
А.
Для определения производной от тока
![]() в момент коммутации
в момент коммутации
![]() продифференцируем по
продифференцируем по
![]() правую и левую части второго выражения
исходной системы уравнений:
правую и левую части второго выражения
исходной системы уравнений:
![]()
![]()
Так как
![]() следовательно
следовательно
![]() В/с.
В/с.
Тогда
![]() В/с.
В/с.
Теперь продифференцируем переходной
ток (2.6.28) по
![]()
![]() .
.
Теперь составим систему из уравнений
(2.6.28) и последнего выражения, записанных
при
![]()
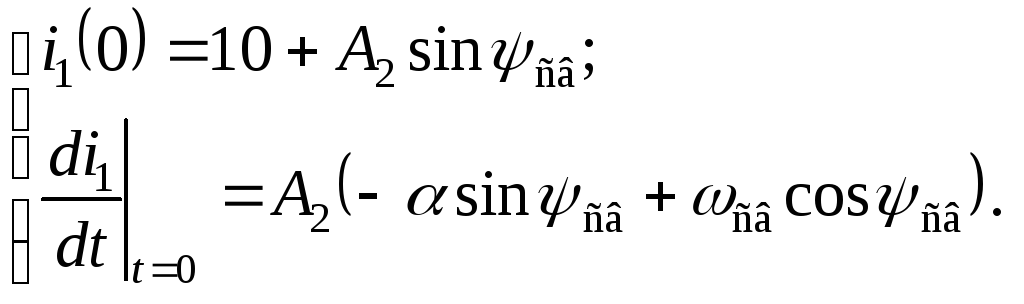
используя полученные зависимые начальные условия окончательно получим систему из двух уравнений с двумя неизвестными:
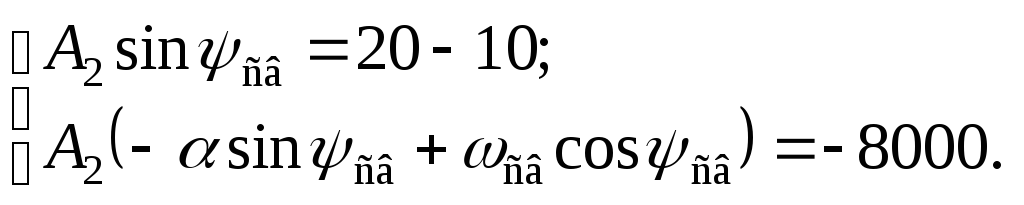
Выразив из первого уравнения этой
системы
![]() и подставив во второе уравнение, получим:
и подставив во второе уравнение, получим:
![]()
![]()
Итак, искомый ток
![]() А.
А.
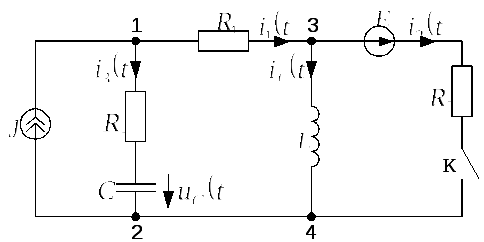
Задача 2.6.5 В цепи, представленной
на рис. 2.6.5.а, в момент
![]() происходит замыкание ключа К в ветви с
резистором
происходит замыкание ключа К в ветви с
резистором
![]() Определить токи
Определить токи
![]() и
и
![]() если известно
если известно
![]() Гн,
Гн,
![]() мкФ,
мкФ,
![]() Ом,
Ом,
![]() Ом,
Ом,
![]() В,
В,
![]() В.
В.
|
|
|
|
Рис. 2.6.5.а |
Рис. 2.6.5.б |
Решение
1) Цепь до коммутации
![]() вычерчена на рис. 2.6.4.б. Постоянный ток
в заряженном конденсаторе
вычерчена на рис. 2.6.4.б. Постоянный ток
в заряженном конденсаторе
![]() следовательно
следовательно
![]()
Используя второй закон коммутации и
исходные данные задачи напряжение на
конденсаторе
![]()
![]() В.
В.
Составим уравнение по второму закону
Кирхгофа для контура, не содержащего
источника тока, учтя, что падение
напряжения на индуктивном элементе от
постоянного тока нет
![]()
![]()
или
![]()
откуда
![]() А.
А.
Тогда
![]() А.
А.
2) Для расчета неизвестных токов
![]() и
и
![]() найдем еще их значения при
найдем еще их значения при
![]() а также величину ЭДС
а также величину ЭДС
![]() Для цепи, изображенной на рис. 2.6.5.а, в
момент замыкания ключа К составим
систему из четырех уравнений, составленных
при
Для цепи, изображенной на рис. 2.6.5.а, в
момент замыкания ключа К составим
систему из четырех уравнений, составленных
при
![]() первое – по первому закону Кирхгофа
для узла “1”, а второе – по первому
закону Кирхгофа для узла “3”, третье –
по второму закону Кирхгофа для контура
первое – по первому закону Кирхгофа
для узла “1”, а второе – по первому
закону Кирхгофа для узла “3”, третье –
по второму закону Кирхгофа для контура
![]() четвертое – в соответствии со вторым
законом Кирхгофа для контура
четвертое – в соответствии со вторым
законом Кирхгофа для контура
![]()
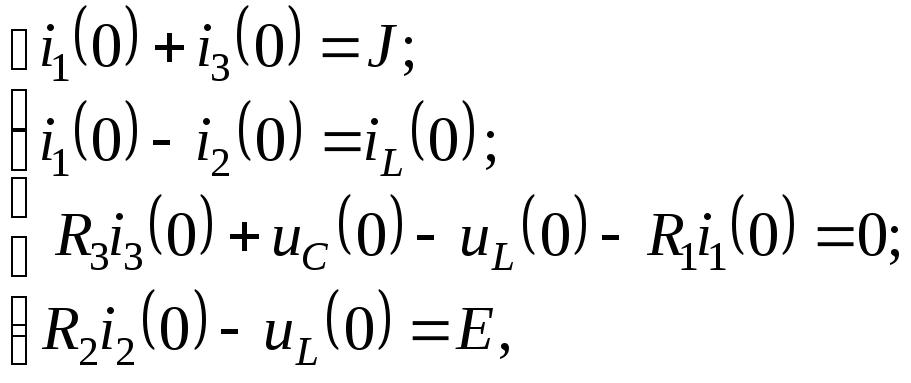
где
![]() А – по первому закону коммутации.
А – по первому закону коммутации.
Выразив из первого уравнения приведенной
системы ток
![]() и подставив во второе уравнение, получим
и подставив во второе уравнение, получим
![]()
Учитывая, что по первому закону коммутации
ток в индуктивности
![]() последнее уравнение примет вид:
последнее уравнение примет вид:
![]()
откуда получаем:
![]()
Кроме того можно записать:
![]()
Теперь подставим две последних формулы в третье уравнение исходной системы:
![]()
Следовательно,
![]() А.
А.
Тогда из четвертого уравнения системы рассчитаем величину ЭДС:
![]() В.
В.
3) Расчет схемы в установившемся режиме
![]() Схема, соответствующая этому режиму
приведена на рис. 2.6.5.в. Катушка
индуктивности закорочена, поэтому по
закону Ома ток
Схема, соответствующая этому режиму
приведена на рис. 2.6.5.в. Катушка
индуктивности закорочена, поэтому по
закону Ома ток
|
|
Ветвь с конденсатором разорвана, поэтому имеем:
Из контура
|
|
Рис. 2.6.5.в |
![]() В.
В.
|
|
4) Для
определение характеристического
уравнения составим схему для свободных
составляющих в момент замыкания ключа
К. При этом
уравнений: первое – на основании первого закона Кирхгофа для узла “1”, второе – по второму закону Кирхгофа для контура |
|
Рис. 2.6.5.г |
![]() третье – по второму закону Кирхгофа
для контура
третье – по второму закону Кирхгофа
для контура
![]()
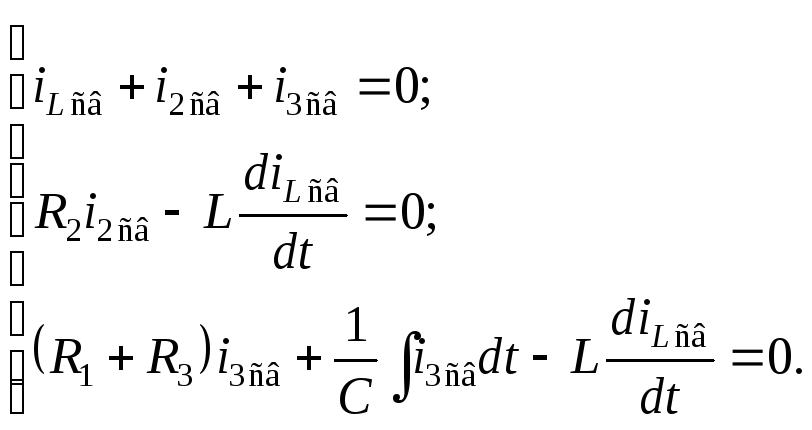
Решим представленную систему относительно
тока
![]() следующим образом.
следующим образом.
Из второго уравнения выразим ток
![]()
|
|
(2.6.30) |
Подставим (4.4.30) в первое уравнение системы:
![]()
Откуда
![]()
Подставим это выражение в третье уравнение исходной системы:
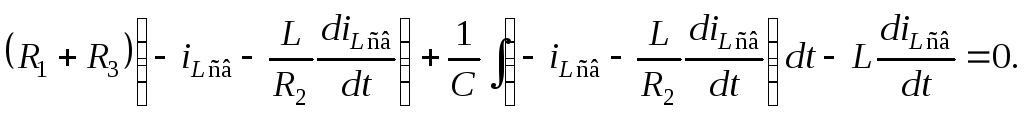
Для того чтобы избавиться от интеграла
продифференцируем правую и левые части
последнего выражения по
![]()
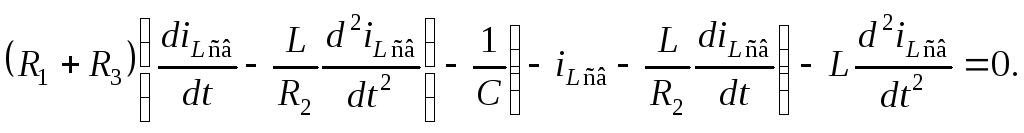
Умножив обе части этого выражения на
множитель
![]() раскрыв скобки и сгруппировав слагаемые
получим ОДУ второго порядка:
раскрыв скобки и сгруппировав слагаемые
получим ОДУ второго порядка:
![]()
Тогда характеристическое уравнение будет иметь следующий вид:
![]()
![]()
![]()
или
![]()
Определим корни характеристического уравнения:
![]() с-1.
с-1.
Общее решение для тока
![]() в случае пары комплексно – сопряженных
корней представим в виде:
в случае пары комплексно – сопряженных
корней представим в виде:
|
|
(2.6.31) |
Для нахождения постоянных интегрирований
запишем напряжение
![]() через ток (2.6.31):
через ток (2.6.31):
![]() ;
;
![]() .
.
Теперь составим систему из выражения (2.6.31) и последнего уравнения:

При
![]() получаем:
получаем:
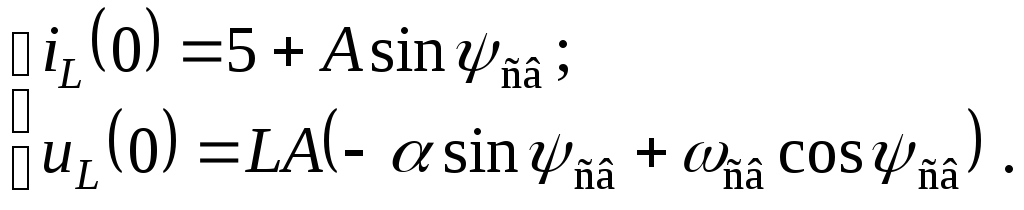
Подставив сюда известные слагаемые
![]() А и
А и
![]() В,
окончательно получим:
В,
окончательно получим:
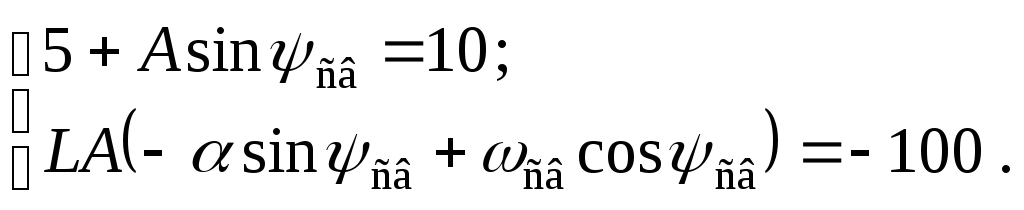
Путем подстановки
![]() во второе уравнение последней системы
определяем постоянные интегрирования:
во второе уравнение последней системы
определяем постоянные интегрирования:
![]()
![]()
Подставив найденные величины в (2.6.31) окончательно получаем:
![]() А.
А.
Ток
![]() представим в виде:
представим в виде:
![]() А.
А.
По соотношению (2.6.30) определим свободную
составляющую
![]()
![]()
![]() В.
В.
Тогда полный переходной ток
![]() В.
В.
З![]() адача
2.6.6Цепь, изображенная на рис. 2.6.6.а,
питается от источника постоянного
напряжения с ЭДС
адача
2.6.6Цепь, изображенная на рис. 2.6.6.а,
питается от источника постоянного
напряжения с ЭДС
![]() В. В момент
В. В момент
![]() происходит замыкание ключа К, в результате
которого в цепь включается источник
синусоидального напряжения с ЭДС
происходит замыкание ключа К, в результате
которого в цепь включается источник
синусоидального напряжения с ЭДС
![]() В. Определить закон изменения тока
В. Определить закон изменения тока
![]() Параметры цепи:
Параметры цепи:
![]() Ом,
Ом,
![]() мГн,
мГн,
![]() мкФ.
мкФ.
|
|
|
|
Рис. 2.6.6.а |
Рис. 2.6.6.б |
Решение
1) Цепь до коммутации
![]() цепь представлена на рис. 2.6.6.б Учитывая
тот факт, что в цепи действует источник
постоянного тока, то
цепь представлена на рис. 2.6.6.б Учитывая
тот факт, что в цепи действует источник
постоянного тока, то
![]()
![]()
Тогда в соответствии с законом Ома
рассчитаем ток
![]() и напряжение
и напряжение
![]()
![]() А;
А;
![]() В.
В.
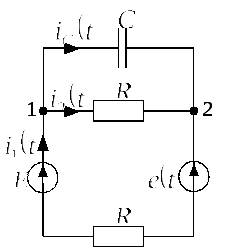
После замыкания ключа К схема распадается
на две подсхемы, изображенные на рис.
2.6.6.в и 2.6.6.г соответственно, переходные
процессы в которых будут происходить
независимо друг от друга. Тогда ток
![]() будет определяться в соответствии с
законом
будет определяться в соответствии с
законом
|
|
|
Кирхгофа для узла “3” как:
Для этого определим эти переходные токи согласно схемам 2.6.6.в и 2.6.6.г. 2)
Рассчитаем ток
|
|
Рис. 2.6.6.в |
Рис. 2.6.6.г |
![]() А.
А.
Составим уравнение по второму закону Кирхгофа:
![]()
Приравняв правую часть этого уравнения к нулю получим ОДУ первого порядка:
![]()
Характеристическое уравнение имеет вид:
![]()
Это уравнение имеет один нулевой корень
![]()
Общее решение для тока
![]() в случае одного корня характеристического
уравнения имеет вид:
в случае одного корня характеристического
уравнения имеет вид:
![]() А.
А.
Так как корень
![]() то второе слагаемое правой части
равняется
то второе слагаемое правой части
равняется
![]() Тогда
Тогда
![]() А.
А.
Для нахождения постоянной интегрирования
![]() запишем это уравнение при
запишем это уравнение при
![]()
![]()
где
![]() А – по первому закону коммутации.
Следовательно,
А – по первому закону коммутации.
Следовательно,
![]()
Итак, ток
![]() А.
А.
3) Найдем ток в ветви с источником
постоянного ЭДС
![]() в соответствии с подсхемой, вычерченной
на рис. 2.6.6.г.
в соответствии с подсхемой, вычерченной
на рис. 2.6.6.г.
|
|
|
Найдем
принужденную составляющею тока
Ток
где
обусловленная действием |
|
Рис. 2.6.6.д |
Рис. 2.6.6.е |
постоянного ЭДС
![]()
![]() переменная
составляющая от действия синусоидальной
ЭДС
переменная
составляющая от действия синусоидальной
ЭДС
![]()
В соответствии со схемой, показанной
на рис. 2.6.6.д рассчитаем ток
![]() Так как постоянная составляющая тока
в конденсаторе
Так как постоянная составляющая тока
в конденсаторе
![]() то в соответствии с законом Ома ток
то в соответствии с законом Ома ток
![]() А.
А.
Теперь рассчитаем синусоидальную
составляющую тока
![]() в соответствии со схемой, представленной
на рис. 2.6.6.е. Комплекс тока
в соответствии со схемой, представленной
на рис. 2.6.6.е. Комплекс тока
 А.
А.
Тогда
![]() А.
А.
Полный ток равен сумме частичных:
![]() А.
А.
Для расчета переходного тока
![]() составим исходную систему уравнений:
составим исходную систему уравнений:
|
|
(2.6.32) |
|
(2.6.33) | |
|
(2.6.34) |
Решим ее относительно искомого тока
![]() способом подстановки. Из (2.6.34) выразим
способом подстановки. Из (2.6.34) выразим
![]()
![]()
Подставим его в (1) и найдем
![]()
![]()
|
|
(2.6.35) |
Подставим (2.6.35) в (2.6.33):
![]()
Чтобы избавиться от интеграла,
продифференцируем по
![]() левую и правую части выражения:
левую и правую части выражения:
![]()
После упрощений получаем НДУ первого порядка:
|
|
(2.63.6) |
ОДУ имеет вид:
![]()
![]()
Составим характеристическое уравнение и найдем его корень:
![]()
![]() с-1.
с-1.
Тогда общее решение НДУ (2.6.36) запишем в виде:
![]() А.
А.
Постоянную интегрирования
![]() найдем, записав последнее уравнение
при
найдем, записав последнее уравнение
при
![]()
![]()
где
![]() начальный ток, который можно определить
из уравнения (2), записанного при
начальный ток, который можно определить
из уравнения (2), записанного при
![]()
![]()
![]() А.
А.
Здесь
![]() В – по второму закону коммутации;
В – по второму закону коммутации;
![]() В.
В.
Тогда имеем:
![]()
Окончательно получим:
![]() А.
А.
Тогда по закону Ома определим ток
![]()
![]() А.
А.
Для расчета суммы двух синусоид
![]() воспользуемся символическим методом.
Сначала определим комплексные изображения
этих синусоид:
воспользуемся символическим методом.
Сначала определим комплексные изображения
этих синусоид:
![]()
![]()
Тогда геометрическая сумма этих двух комплексов
![]()
Следовательно,
![]()
Окончательно
![]() А.
А.
Проверка:
При
![]()
![]() А.
А.
На основании первого закона Кирхгофа
для узла “3”, записанного при
![]() получаем тот же ток:
получаем тот же ток:
![]() А.
А.
Это говорит о том, что ток
![]() найден верно.
найден верно.
2.7 Примеры расчета переходных процессов при “неккоректных” коммутациях
Задача 2.7.1Цепь, изображенная на
рис. 2.7.1.а, питается от источника
постоянного напряжения![]() В. Определить ток
В. Определить ток![]() и напряжение
и напряжение![]() после размыканию ключа К. Параметры
цепи:
после размыканию ключа К. Параметры
цепи:![]() Ом,
Ом,![]() Ом,
Ом,![]() Гн,
Гн,![]() Гн,
Гн,![]() Гн.
Гн.
|
|
|
|
Рис. 2.7.1.а |
Рис. 2.7.1.б |
Решение
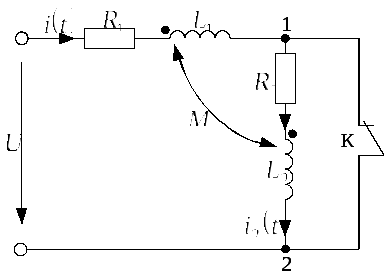
1) Цепь до коммутации представлена на
рис. 2.7.1.б. Катушка с индуктивностью
![]() зашунтирована ключом К, поэтому ее ток
зашунтирована ключом К, поэтому ее ток
![]()
По закону Ома определяем ток в цепи:
![]() А.
А.
|
|
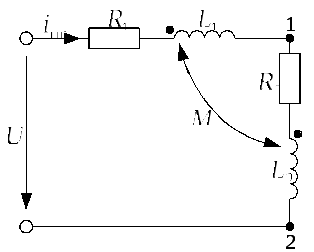
2) Схема после коммутации вычерчена на рис. 2.7.1.в. На постоянном токе индуктивной связи между катушками и падения напряжения на индуктивных элементах нет, поэтому по закону Ома для участка цепи ток
3) Для цепи, изображенной на рис. 2.7.1.а, в момент коммутации составим уравнение по второму закону Кирхгофа с учетом согласного включения катушек:
|
|
Рис. 2.7.1.в |
иначе
![]()
Приравняв правую часть данного НДУ первого порядка к нулю получим ОДУ:
![]()
откуда составим характеристическое уравнение:
![]()
Определим его корень:
![]() с-1.
с-1.
Тогда общее решение НДУ имеет вид:
![]()
Для определения
![]() запишем последнее выражение при
запишем последнее выражение при![]()
![]()
Для нахождения
![]() воспользуемся обобщенными законам
коммутации, т.е. условием непрерывности
потокосцепления (потокосцепление в
момент коммутации любого контура равно
алгебраической сумме потокосцеплений
всех входящих в него элементов):
воспользуемся обобщенными законам
коммутации, т.е. условием непрерывности
потокосцепления (потокосцепление в
момент коммутации любого контура равно
алгебраической сумме потокосцеплений
всех входящих в него элементов):
![]()
Учитывая, что
![]() получим
получим
![]() А.
А.
Тогда имеем:
![]()
![]()
Окончательно получаем,
![]() А.
А.
Найдем напряжение
![]()
![]() В.
В.
Задача 4.7.2Цепь, представленная на
рис. 2.7.2.а подключена к источнику
синусоидального напряжения![]() В. В момент
В. В момент![]() происходит замыкание ключа К. Известны
следующие параметры цепи:
происходит замыкание ключа К. Известны
следующие параметры цепи:![]() Ом,
Ом,![]() Гн. Найти токи
Гн. Найти токи![]() и
и![]() после замыкания ключа К.
после замыкания ключа К.
|
|
|
|
|
Рис. 2.7.2.а |
Рис. 2.7.2.б |
Рис. 2.7.2.в |
Решение
1) Цепь до коммутации изображена на рис. 2.7.2.б. Здесь ток
![]()
Для расчета воспользуемся символическим методом. Предварительно найдем индуктивное сопротивление и комплекс напряжения источника:
![]() Ом;
Ом;
![]() В.
В.
Тогда в соответствии с законом Ома рассчитываем комплекс тока в цепи:
![]() А.
А.
Тогда его мгновенное значение определиться как:
![]() А.
А.
2) Схема, соответствующая работе цепи
после коммутации приведена на рис.
2.7.2.в. Пользуясь символическим методом
рассчитаем токи в ветвях с катушками
![]() и
и![]() Эквивалентное комплексное сопротивление
цепи
Эквивалентное комплексное сопротивление
цепи
![]()
Ток во входной ветви
![]()
Согласно методу “чужой” ветви определяем искомые комплексы токов:
![]()
![]() А.
А.
Тогда запишем мгновенные значения этих токов:
![]() А.
А.
3) С целью расчета переходного процесса для цепи, представленной на рис. 2.7.2.а, в момент срабатывания ключа К составляем исходную систему уравнений по законам Кирхгофа:
|
|
(2.7.1) |
Решим представленную систему относительно
тока
![]()
Из второго уравнения системы (2.7.1) выразим ток
|
|
(2.7.2) |
Подставим (2.7.2) в первое уравнение системы
(2.7.1) и выразим из получившегося выражение
ток
![]()
![]()
![]()
Подставим последний ток в третье уравнение системы (2.7.2):
![]()
![]()
После упрощений получаем НДУ второго порядка:
![]()
Отсюда находим ОДУ и характеристическое уравнение:
![]()
![]()
Определим корни характеристического уравнения:
![]()
![]() с-1.
с-1.
Характеристическое уравнение имеет один нулевой корень и один отрицательный ( переходной процесс имеет апериодический характер “как бы” второго порядка). Тогда общее решение НДУ будет иметь вид:
![]()
Ввиду равенства нулю корня
![]() получаем:
получаем:
|
|
(2.7.3) |
Для нахождения постоянных интегрирования
![]() и
и![]() найдем производную от последнего
выражения:
найдем производную от последнего
выражения:
![]()
Запишем это соотношение при
![]()
|
|
(2.7.4) |
Найдем значение
![]() Для этого перепишем исходную систему
уравнений (2.7.1) для
Для этого перепишем исходную систему
уравнений (2.7.1) для![]()
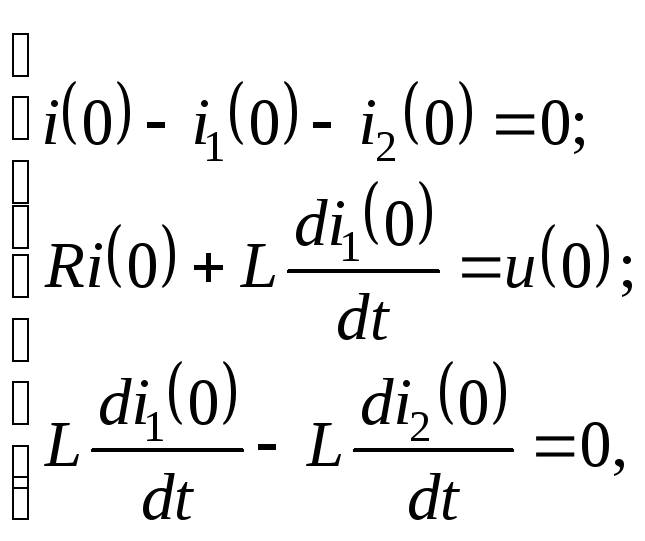
где
![]() и
и![]() – независимые начальные условия,
определяемые по первому закону коммутации:
– независимые начальные условия,
определяемые по первому закону коммутации:
![]() А;
А;
![]()
Тогда из последней системы уравнений следует, что:
![]() А;
А;
![]()
Запишем уравнение (2.7.2) при
![]()
![]()
Тогда
![]() А/с.
А/с.
Из уравнения (2.7.4) определяем постоянную
интегрирования
![]()
![]()
Запишем общее решение НДУ (2.7.3) при
![]()
![]()
Откуда,
![]()
Таким образом, ток
![]() изменяется по следующему закону:
изменяется по следующему закону:
![]() А.
А.
Общее выражения для тока
![]() аналогично соотношению (4.7.3):
аналогично соотношению (4.7.3):
|
|
(2.7.5) |
Для нахождения постоянных интегрирования
![]() и
и![]() найдем производную от последнего
выражения:
найдем производную от последнего
выражения:
![]()
Запишем это соотношение при
![]()
![]()
Тогда
![]()
Запишем (2.7.5) при
![]()
![]()
Откуда,
![]()
Итак, ток
![]() изменяется по следующему закону:
изменяется по следующему закону:
![]() А.
А.
Задача 2.7.3В цепи, представленной
на рис. 2.7.3.а с параметрами![]() Ом,
Ом,![]() мГн,
мГн,![]() мкФ,
мкФ,![]() мкФ, в момент
мкФ, в момент![]() происходит срабатывание ключа К.
Определить напряжение на конденсаторе
происходит срабатывание ключа К.
Определить напряжение на конденсаторе![]() после замыкания ключа, если до коммутации
конденсатор с емкостью
после замыкания ключа, если до коммутации
конденсатор с емкостью![]() был заряжен до напряжения
был заряжен до напряжения![]() В.
В.
|
|
|
|
Рис. 2.7.3.а |
Рис. 2.7.3.б |
Решение
1) Рассчитаем цепь до коммутации.
Напряжение на конденсаторе с емкостью
![]() по условию задачи
по условию задачи
![]() В.
В.
Напряжение на конденсаторе с емкостью
![]() и ток в катушке индуктивности соответственно
равны:
и ток в катушке индуктивности соответственно
равны:
![]()
![]()
2) Расчет схемы после коммутации (схема
вычерчена на рис. 2.7.3.б). Постоянный ток
в конденсаторе
![]() Также напряжение на индуктивном элементе
Также напряжение на индуктивном элементе![]() Тогда, в соответствии со вторым законом
Кирхгофа для схемы, приведенной на рис.
2.7.3.б, напряжение на конденсаторе
Тогда, в соответствии со вторым законом
Кирхгофа для схемы, приведенной на рис.
2.7.3.б, напряжение на конденсаторе![]() уравновешивается напряжением на другом
конденсаторе
уравновешивается напряжением на другом
конденсаторе![]() Для расчета этого напряжения можно
воспользоваться законом сохранения
заряда:
Для расчета этого напряжения можно
воспользоваться законом сохранения
заряда:
|
|
(2.7.6) |
Так как заряды до коммутации
![]() и
и![]() можно представить как:
можно представить как:
![]()
![]()
то условие (2.7.6) можно записать следующим образом:
![]()
или
![]()
Теперь составим систему из двух последних уравнений:
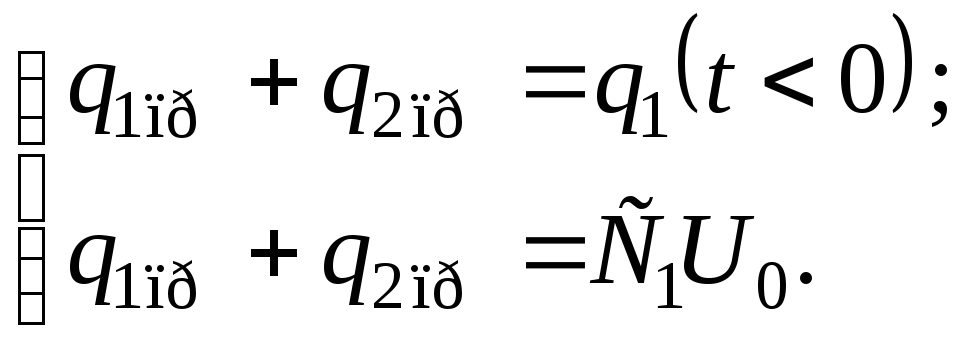
Выразив из первого уравнения данной
системы заряд
![]() и подставив во второе уравнение, получаем:
и подставив во второе уравнение, получаем:
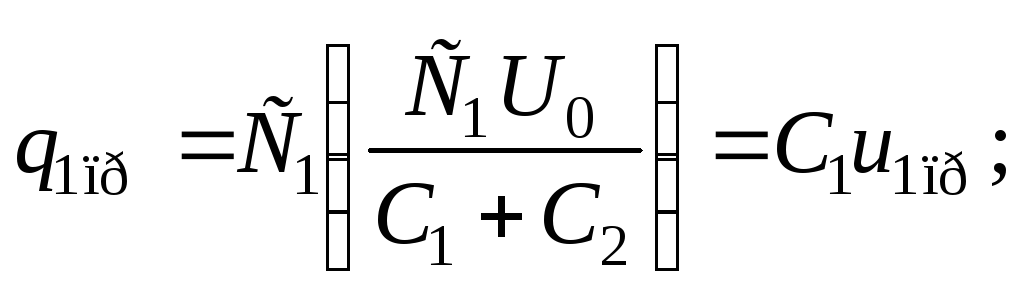
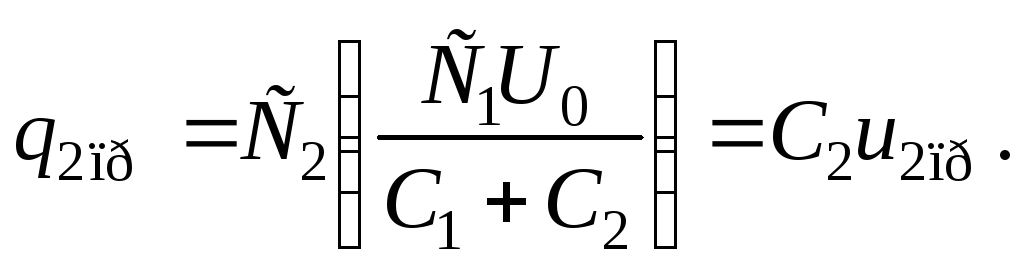
Отсюда находим принужденные составляющие напряжений на конденсаторах:
![]() В.
В.
3) Расчет переходного процесса
![]() Для цепи, приведенной на рис. 2.7.3.а (ключ
К замкнут) составим уравнение по второму
закону Кирхгофа:
Для цепи, приведенной на рис. 2.7.3.а (ключ
К замкнут) составим уравнение по второму
закону Кирхгофа:
|
|
(2.7.7) |
где
![]()
|
|
(2.7.8) |
Решим это уравнение относительно
напряжения
![]() для этого напряжение
для этого напряжение![]() представим следующим образом:
представим следующим образом:
![]()
Тогда уравнение (2.7.7) с учетом приведенных здесь соотношений можно записать следующим образом:
![]()
После упрощений имеем НДУ второго порядка:
![]()
ОДУ имеет вид:
![]()
Отсюда составляем характеристическое уравнение:
![]()
![]()
![]()
Определяем его корни:
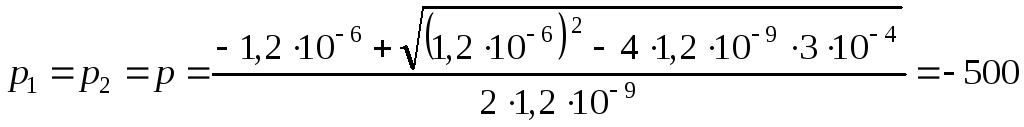 с-1.
с-1.
Так как корни характеристического уравнения получаются комплексно – сопряженными, то общее решение НДУ представим в виде:
![]()
Для нахождения постоянной интегрирования
![]() запишем это выражение при
запишем это выражение при![]()
![]()
где
![]() В – по второму закону коммутации.
В – по второму закону коммутации.
Тогда
![]() В.
В.
Для нахождения
![]() продифференцируем общее решение НДУ:
продифференцируем общее решение НДУ:
![]()
В частности при
![]() имеем:
имеем:
![]()
Для нахождения значения
![]() запишем выражение (2.7.8) при
запишем выражение (2.7.8) при![]()
![]()
Следовательно,
![]()
Тогда
![]()
Таким образом, напряжение на конденсаторе
с емкостью
![]() изменяется по следующему закону:
изменяется по следующему закону:
![]() В.
В.

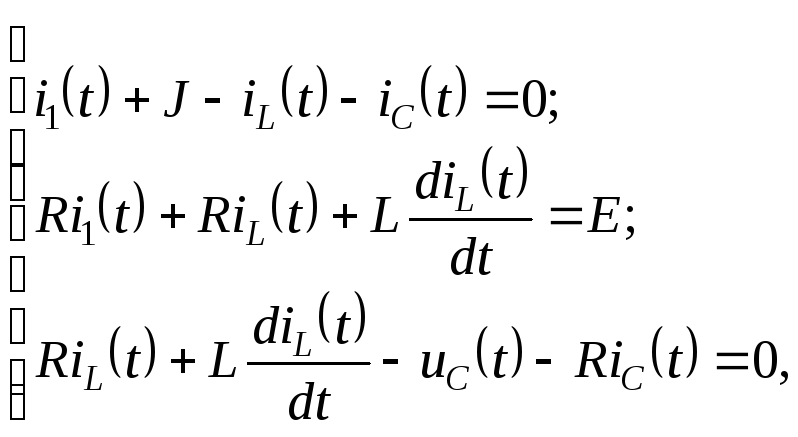
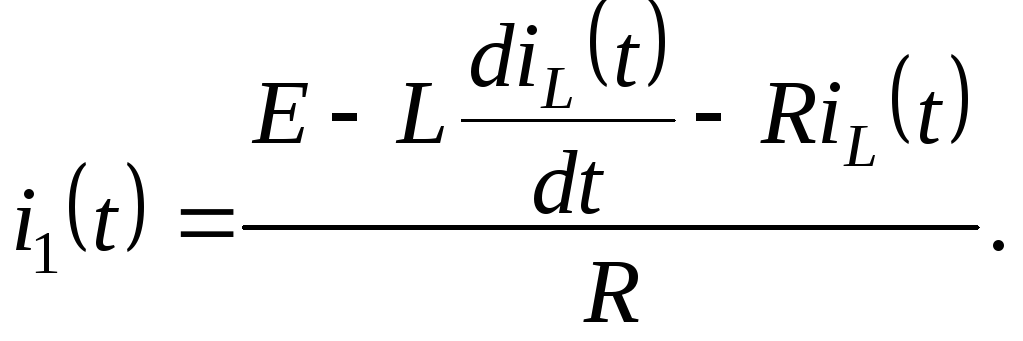
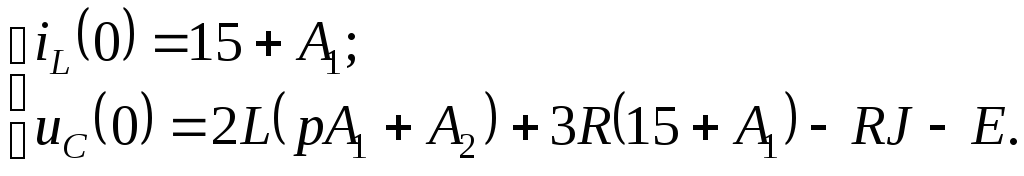




 А;
А;