Задание 1

a) Наберите программуMultikи измените скорость перемещения окружности с помощью варьируемых параметров так, чтобы окружность плавно перемещалась.

б) Организуйте движение второй окружности с независимыми от первой параметрами.

Задание 2

а) Наберите программу Salutи модифицируйте ее так, чтобы вместо окружности перемещался бы эллипс, все параметры которого также зависели бы от случайных чисел.

б) Модифицируйте программу так, чтобы вместо эллипса перемещалась бы прямая, координаты и цвет которой зависели бы также от случайных чисел.

Тема 17 Численные методы вычисления определённого интеграла

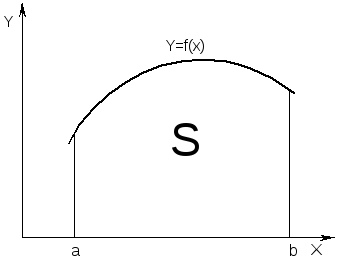
При решении инженерных задач часто приходится вычислять значения определённого интеграла. В случаях, когда не удаётся выразить интеграл в замкнутой форме, или полученная формула сложна, или подынтегральная функция задана таблично, пользуются численным интегрированием. В основе численного интегрирования лежит приближенное вычисление площади под кривой, описываемой подынтегральной функцией. В общем виде задача формулируется как нахождение значения

^.

Наиболее простыми для реализации являются методы, для которых значения xзаданы с постоянным шагом. Мы рассмотрим методы прямоугольников, трапеций (Ньютона-Котеса) и парабол (Симпсона).

В общем виде алгоритм решения задачи состоит из шагов:

1. Интервал, на котором выполняется интегрирование [a,b], разбивается наnравных отрезков и вычисляется длина этих отрезков;

2. Криволинейная трапеция Sзаменяется фигурой, составленных, в зависимости от метода, из элементарных прямоугольников, трапеций, или криволинейных трапеций;

3. Вычисляются и суммируются площади S_iкаждой элементарной фигуры.

1. Метод прямоугольников

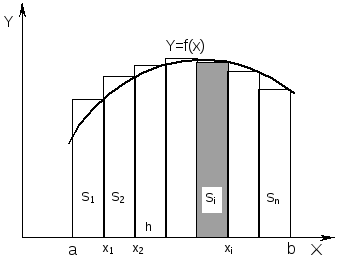
Пусть на отрезке [a,b] задана непрерывная функцияy=f(x), см. рис.17.1. Интервал, на котором выполняется интегрирование[a,b], разбивается наnравных отрезков, и криволинейная трапецияSзаменяется фигурой, составленной из элементарных прямоугольников с площадямиS_i., рис.17.2.

Шаг интегрирования

Площадь элементарной фигуры

Интеграл равен

Рис.17.1. Геометрический смысл определённого интеграла	Рис.17.2. Интегрирование методом прямоугольников

Таким образом, для вычисления определённого интеграла методом прямоугольников достаточно вычислить сумму значений подынтегральной функции в узлах интегрирования и умножить эту сумму на шаг интегрирования. Преимуществом метода является его простота, недостатком – сравнительно невысокая точность, для повышения которой необходимо увеличивать значение nдо 1...10 тысяч.

Пример 1. Составить программу для вычисления интегралас заданным количеством узлов интегрированияn. Аналитическое решение даёт результат 9,0. Таким образом, при условии правильного составления программы ожидаемый результат должен быть примерно равен 9. Большое число десятичных знаков при выводе результата позволяет оценить точность метода.

Program Integral1;

Uses Crt;

Var

a,b,s,x,h:real;

i, n: integer;

Function f(xx:real):real;

begin

f:=xx*xx; {Здесь приводим выражение для вычисления функции }

end;

Begin

ClrScr;

Writeln(' Вычисление определенного интеграла');

Writeln(' Метод прямоугольников');

{ Ввод исходных данных }

a:=0; b:=3; n:=1000;

{ Начинаем расчет }

h:=(b-a)/n;

s:=0; x:=a;

for i:=1 to n do

begin

x:=x+h;

s:=s+f(x);

end;

s:=s*h;

Writeln(' Интеграл равен ', s:10:7);

Readln;

End.