Тема 18 Численные методы решения нелинейных уравнений
При решении инженерных задач встречаются алгебраические и трансцендентные уравнения, что может представлять собой самостоятельную задачу или являться составной частью более сложных задач. В обоих случаях применение численного метода позволяет быстро и эффективно добиться решения задачи.
Линейные уравнения имеют одно решение, алгебраические уравнения – nрешений, трансцендентные – неопределённое число решений. Решение линейных уравнений с одним неизвестным является достаточно простой задачей и здесь не рассматривается.
Уравнения, содержащие
только суммы целых степеней x,называются алгебраическими. Их общий
вид
.
Нелинейные уравнения, содержащие тригонометрические функции или другие специальные функции, например, lg xилиex, называются трансцендентными.
Для решения нелинейных уравнений, для которых отсутствует аналитическое решение или оно очень сложно, применяют численные методы, в которых, как правило, применяются итерационные алгоритмы. В итерационных методах задаётся процедура решения в виде многократного применения некоторого алгоритма. Полученное решение всегда является приближённым, хотя может быть сколь угодно близким к точному.
В общем случае задача формулируется следующим образом.
Пусть на отрезке [a,b]дана непрерывная функцияy=f(x), причем значенияf(a)иf(b)имеют разные знаки. Тогда абсцисса точки пересечения графика функцииy=f(x)с осьюXбудет корнем уравненияf(x)=0, см. рис.18.1. Другими словами, требуется найти такое значениеx, при котором значение функцииf(x)будет равно нулю.
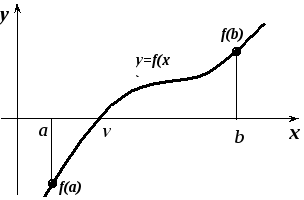
Рис.18.1. Графическая интерпретация нахождения корня уравнения
Численными методами значение корня определяется с погрешностью, не превосходящей данного положительного, достаточно малого числа . Иначе говоря, еслиv– истинное значение корня, при которомf(v)=0, то требуется определить такое числоw, при которомawbиvw.
Первый этап решения состоит в отыскании области существования корня, т.е. отрезков на оси абсцисс, в концах которых функция имеет разные знаки. Для этого вычисляются значения функции в точках, расположенных через равные интервалы на оси x. Это делается до тех пор, пока не будут найдены два последовательных значения функцииf(xn)иf(xn+1), имеющих противоположные знаки, т.е.f(xn)f(xn+1)<0. Таким образом, приa= xn,b=xn+1, уточнение корней будет производиться на отрезке[a,b].
Для решения данной задачи применяются методы: половинного деления, касательных (Ньютона), хорд и секущих.
Метод половинного деления
Алгоритм метода состоит из следующих операций.
Отрезок [a,b]делят пополам точкойc,c=(a+b)/2, и находят значение функции в точкес. Еслиf(c)=0, то корень уравнения соответствует точкеc. Еслиf(c)0, то можно сузить диапазон поиска корня: перейти от отрезка[a,b]к отрезку[a,c]или[c,b]в зависимости от знакаf(c). Еслиf(a)f(c)<0, то корень находится на отрезке[a,c], и точкусбудем считать точкойb; а еслиf(a)f(c)>0, то корень находится на отрезке[c,b], и точкусбудем считать точкойa.
Каждый такой шаг уменьшает в два раза интервал, в котором находится корень уравнения f(x)=0. После нескольких шагов получится отрезок, длина которого будет меньше или равна числу, т.е.ab. Любая точка такого отрезка, например, один из его концов, подходит в качестве решения поставленной задачи. На рис. 18.2. показано несколько этапов применения алгоритма.
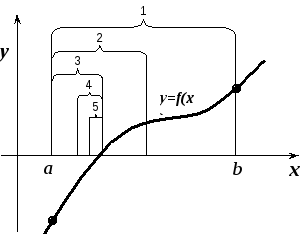
Рис.18.2. Графическая иллюстрация метода половинного деления: 1…5 – интервалы уточнения корней на 1..5 шаге алгоритма
Пример 1. Найти с точностью=0,001на отрезке[-2,1]корень уравненияx3+x2+x+1=0. Приведём текст программы, которая решает эту задачу методом половинного деления. Результат выводится на экран, и, по желанию пользователя, на принтер.
Program Popolam;
Uses Crt, Printer;
Var
a,b,c,eps,a0,b0:real;
k:integer;
ch:char;
Function f(x:real):real;
begin
{Здесь приводим выражение для вычисления функции }
f:=x*x*x+x*x+x+1;
end;
Begin
ClrScr;
Writeln(' Решение уравнения методом половинного деления ');
{ Ввод исходных данных }
a:=-2; b:=1; eps:=0.001;
a0:=a; b0:=b; { запоминаем исходные данные }
{ Начинаем расчет }
k:=0; { Счетчик повторений }
While abs(b-a)>=eps do
begin
k:=k+1;
c:=(a+b)/2;
if f(a)*f(c)<=0 then b:=c
else a:=c;
end;
Writeln(' Уравнение x^3+x^2+x+1=0 на отрезке [',a0:4:1, ',', b0:4:1, '] имеет корень x = ', c:10:8);
Writeln(' f(x) = ',f(c):10:8);
Writeln('Точность ',eps:10:8, ' достигнута за ', k,' итераций');
Write(' Печатать результаты на принтере? (Y/N)');
Repeat
ch:=ReadKey;
ch:= UpCase(ch);
Until (ch='Y') or (ch='N');
if ch='Y' then
begin
Writeln(lst,'Решение уравнения методом половинного деления');
Writeln(lst,' Уравнение x^3+x^2+x+1=0 на отрезке [', a0:4:1, ',', b0:4:1, '] имеет корень x = ', c:10:8);
Writeln(lst,' f(x) = ',f(c):10:8);
Writeln(lst,' Точность ',eps:10:8, ' достигнута за ', k,' итераций');
Writeln('Печать выполнена. НажмитеENTER ');
Readln;
end;
End.
Метод Ньютона
В отличие от метода половинного деления, для определения интервала, в котором заключён корень, не требуется находить значения функции с противоположными знаками. Вместо интерполяции по двум значениям функции, в методе Ньютона осуществляется экстраполяция с помощью касательной к кривой в данной точке. В основе метода лежит разложение функции f(x)в ряд Тейлора
Члены ряда, содержащие hво второй и более высоких степенях, отбрасываются; используется соотношениеxn+h=xn+1. Предполагается, что переход отxnкxn+1приближает значение функции к нулю так, чтоf(xn+h)=0. Тогдаxn+1=xn f(xn)/ f`(xn).
Значение xn+1соответствует точке, в которой касательная к кривой в точкеxnпересекает осьx. Так как криваяf(x)отлична от прямой, то значение функцииf(xn+1)не будет в точности равно нулю. Поэтому вся процедура повторяется, причём вместоxnиспользуетсяxn+1. Счет прекращается, когда разница междуxnкxn+1будет меньше или равна числу, т.е. xn xn+1.
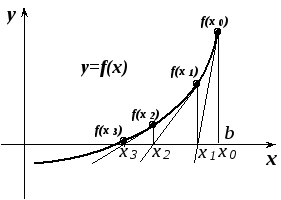
Рис. 18.3. процесс решения уравнения методом Ньютона
На рис. 18.3. процесс решения уравнения методом Ньютона, который ёще называют методом касательных, показан графически.
Пример 2. Приведём фрагменты текста программы, которая решает задачу из примера 1 методом касательных. Ввод и вывод результатов подробно разобран выше.
Program Kasat;
Uses Crt, Printer;
Var
a,b,t,x,eps:real;
Function f(x:real):real;
begin
{Здесь приводим выражение для вычисления функции }
f:=x*x*x+x*x+x+1;
end;
Function f1(x:real):real;
begin
{ Здесь приводим выражение для производной функции }
f:=3*x*x+2*x+1;
end;
Begin
ClrScr;
Writeln(' Решение уравнения методом касательных');
{ Ввод исходных данных }
a:=-2; b:=1; eps:=0.001;
{ Начинаем расчет }
x:=a;
Repeat
t:=f(x)/f1(x);
x:=x-t;
Until abs(t)<=eps;
Writeln(' Уравнение имеет корень x = ', x:10:8);
Readln;
End.
Метод Ньютона требует меньшего числа повторений, чем метод половинного деления. Недостатки метода – необходимость дифференцирования функции f(x), иf(x)должно быть не равно нулю.
Метод хорд
Этот метод ещё имеет название метода ложного положения. В основе метода лежит линейная интерполяция по двум значениям функции f(x), имеющим противоположные знаки. Через точки, соединяющие значения функцииf(a)иf(b)на концах отрезка[a,b], проводят прямую, которая пересекает осьxв точке
.
Значение функции f(x)сравнивается со значениями функцийf(a)иf(b)и в дальнейшем используется вместо того из них, с которым оно совпадает по знаку. Если значениеf(x)недостаточно близко к нулю, то вся процедура повторяется до тех пор, пока не будет достигнута необходимая степень сходимости. На рис.18.4 процесс решения показан графически.
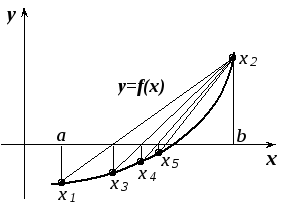
Рис.18.4. Процесс решения уравнения методом хорд
Пример 3. Приведём фрагменты текста программы, которая решает задачу из примера 1 методом хорд.
Program Horda;
Uses Crt;
Var
a,b,t,x,eps:real;
Function f(x:real):real;
begin
{Здесь приводим выражение для вычисления функции }
f:=x*x*x+x*x+x+1;
end;
Begin
ClrScr;
Writeln(' Решение уравнения методом хорд');
{ Ввод исходных данных }
a:=-2; b:=1; eps:=0.001;
{ Начинаем расчет }
Repeat
x:=a-f(a)*(b-a)/(f(b)-f(a));
if f(a)*f(x)<=0 then b:=x
else a:=x;
Until abs(f(x))<=eps;
Writeln(' Уравнение имеет корень x = ', x:10:8);
Readln;
End.