Задания

1. Набрать текст программы Popolam. Провести вычисления и вы вывести на принтер (экран) результаты расчётов при= 0,1; 0,01; 0,0001; 0,00001. Сравнить результат и количество итераций.

2. Сохранить под другим именем и модифицировать программу, чтобы она решала уравнение методом касательных. Сравнить результат и количество итераций при = 0,1; 0,01; 0,001; 0,0001.

3. Сохранить под другим именем и модифицировать программу, чтобы она решала уравнение методом хорд. Сравнить результат и количество итераций при = 0,1; 0,01; 0,001; 0,0001.

4. Сохранить под другим именем и используя три предыдущих примера, модифицировать программу, чтобы последовательно методом половинного деления, хорд и касательных уточнить корень уравнения (см. табл.), расположенный на интервале [a,b], с абсолютной погрешностью. Определить также число итераций, необходимое для нахождения корня. Сравнить результат при= 0,1; 0,01; 0,001; 0,0001; 0,00001. Результаты должны выводиться в виде таблицы

Результаты решения уравнения методами

Точность	Деления пополам	Касательных	Хорд
0,1
0,01
0,001
0,0001
0,00001

Варианты задания

Вариант задания	Уравнение	Отрезок
1	x^2+10x=0	[0; 1]
2	=0	[2; 3]
3	x-2+sin(1/x)=0	[1,2; 2]
4	1 - x + sin x - ln(1+x)=0	[0; 1,5]
5	x^2-ln(1+x)-3=0	[2; 3]
6	2x - 3 ln x - 3=0	[0,5; 0,6]
7	Ln x - x + 1,8=0	[2; 3]
8	0,1x^2-x ln x=0	[1; 2]
9	x+cos(x^0,52+2)=0	[0,5; 1]
10	3x - 4 ln x - 5=0	[2; 4]

Тема 19 Численные методы решения обыкновенных дифференциальных уравнений

Дифференциальными называются уравнения, содержащие одну или несколько производных. Поскольку большая часть законов физики формулируется именно в виде дифференциальных уравнений, то инженеру приходится сталкиваться с ними. Лишь немногие из них удаётся решить без помощи вычислительных машин. Поэтому численные методы решения дифференциальных уравнений играют важную роль в практике инженерных расчётов.

Чтобы решить обыкновенное дифференциальное уравнение, необходимо знать значения зависимой переменной и (или) её производных при некоторых значениях независимой переменной. Если дополнительные условия задаются при одном значении независимой переменной, то такая задача называется задачей с начальными условиями, или задачей Коши. Если же условия задаются при двух или более значениях независимой переменной, то такая задача называетсякраевой. В задаче Коши дополнительные условия называются начальными, а в краевой задача – граничными.

Рассмотрим способы решения задачи Коши, которая формулируется следующим образом. Пусть дано дифференциальное уравнение

и начальное условие y(x₀)=y₀.

Требуется найти функцию y(x), удовлетворяющую как указанному уравнению, так и начальному условию. Искомая функция выражается в табличном виде

x0	x1	x2	x3	…	xn
y0	y1	y2	y3	…	yn

Значения xвычисляются, через малое приращениеh,  h=x₀-x₁=x₂-x₁.

Обычно численное решение этой задачи получают, вычисляя сначала значение производной, а затем, задавая малое приращение для x, переходят к новой точкеx₁=x₀+h. Положение новой точки определяется по наклону кривой, вычисленному с помощью дифференциального уравнения. Таким образом, график численного решения представляет собой последовательность коротких прямолинейных отрезков, которыми аппроксимируется истинная криваяy=f(x), рис.19.1. Сам численный метод определяет порядок действий при переходе от данной точки кривой к следующей.

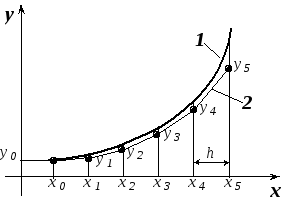
Рис.19.1. Графическое представление численного решения задачи Коши: 1 – точное решение; 2 – решение, полученное численным методом

Наиболее простыми и известными из методов решения задачи Коши являются методы Эйлера и Рунге-Кутта. Они используются для решения дифференциальных уравнений первого порядка вида y=f(x,y), гдеy=dy/dx, при начальном условииy(x₀)=y₀.

Метод Эйлера

Это простейший метод решения задачи Коши, позволяющий решить дифференциальное уравнение первого порядка. Его точность невелика, поэтому на практике им пользуются редко. Однако, на основе этого метода легче понять алгоритм других, более эффективных методов.

Метод Эйлера основан на разложении функции yв ряд Тейлора в окрестностиx₀:

Если hмало, то члены, содержащие производные второго и более высоких порядков, можно отбросить. Тогда.y’(x₀)находим из дифференциального уравнения, подставив в него начальное условие. Таким образом, можно получить приближённое значениеyпри малом смещенииhот начальной точкиx₀. Этот процесс можно продолжить, используя следующую рекуррентную формулу

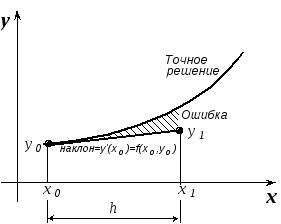
Рис.19.2. Принцип метода Эйлера

y_i+1=y_i + hf(x_i,y_i), i=1,2,…

Графически метод Эйлера показан на рис.19.2. Ошибка метода имеет порядок h².

Пример 1. Составим программу для решения дифференциального уравненияy=2x²+2yпри начальном условииy(0)=1;0 x1иh=0,1.

Program Euler;

Uses Crt;

Var

xn,xk,yn,h,x,y:real;

i:integer;

Function f(x,y:real):real;

begin

{Здесь приводим выражение для вычисления функции f(x,y) }

f:=2*x*x+2*y;

end;

Begin

ClrScr;

Writeln(' Решение дифференциального уравнения ');

Writeln(' dy/dx=2x^2+2y методом Эйлера ');

{ Ввод исходных данных }

xn:=0; yn:=1; xk:=1; h:=0.1;

{ Выводим шапку таблицы и первую точку }

Writeln('--------------------');

Writeln('| № | x | y |');

Writeln('--------------------');

{ Начинаем расчет }

x:=xn; y:=yn; i:=1;

Writeln('|', i:2, ' |', x:5:2, ' |', y:7:4, ' |');

repeat

y:=y+h*f(x,y);

Writeln('|', i:2, ' |', x:5:2, ' |', y:7:4, ' |');

x:=x+h;

i:=i+1;

until x>xk;

Writeln('--------------------');

Readln;

End.

Модифицированный метод Эйлера

Точность метода Эйлера можно существенно повысить, улучшив аппроксимацию производной. Это можно сделать, например, используя среднее значение производной в начале и в конце интервала. В модифицированном методе Эйлера сначала по методу Эйлера вычисляется значение функции в следующей точке:

y^*_i+1 = y_i + hf(x_i,y_i),

которое используется для вычисления приближённого значения производной в конце интервала f(x_i+1, y^*_i+1). Вычислив среднее между этим значением производной и её значением в начале интервала, найдём более точное значениеy_i+1:

y_i+1 = y_i + h/2 f(x_i,y_i) + f(x_i+1, y^*_i+1 )] .

Принцип метода проиллюстрирован на рис. 19.3. Для получения новой точки в нём требуется информация о двух других точках – предыдущей и промежуточной. Ошибка этого метода на каждом шаге имеет порядок h².

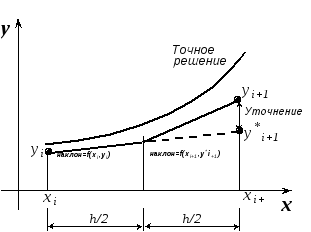
Рис.19.3. Принцип модифицированного метода Эйлера

Пример 2.Разработать, сохранить и выполнить программу для решения дифференциального уравнения из примера 1 модифицированным методом Эйлера. При выполнении расчетов использовать хранение результатов в массивах.

Program ModEuler;

Uses Crt;

Var

xn,xk,yn,yw,h:real;

i,n:integer;

x,y:array [1..20] of real;

Function f(x,y:real):real;

begin

f:=2*x*x+2*y;

end;

Begin

ClrScr;

Writeln(' Решение дифференциального уравнения ');

Writeln(' dy/dx=2x^2+2y модифицированным методом Эйлера ');

xn:=0; yn:=1; xk:=1; h:=0.1;

x[1]:=xn; y[1]:=yn; i:=1;

repeat

yw:=y[i]+h*f(x[i],y[i]);

y[i+1]:=y[i]+h/2*(f(x[i],y[i])+f(x[i]+h,yw));

x[i+1]:=x[i]+h;

i:=i+1;

until x[i]>xk;

n:=i;

{ Выводим результаты }

Writeln('--------------------');

Writeln('| № | x | y |');

Writeln('--------------------');

for i:= 1 to n do

Writeln('|', i:2, ' |', x[i]:5:2, ' |', y[i]:7:4, ' |');

Writeln('--------------------');

Readln;

End.

Метод Рунге-Кутта

Для повышения точности вычисления значений функции требуется проведение дополнительных вычислений внутри интервала h, то есть междуx_i и x_i+1. Метод Рунге-Кутта даёт набор формул для расчёта координат внутренних точек, требуемых для достижения точности, то есть ошибки на каждом шаге, порядкаh⁴. Расчёты при использовании этого метода производятся по формулам:

,

где k₀=hf(x_i,y_i),k₁=hf(x_i+h/2, y_i+k₀/2),k₂=hf(x_i+h/2, y_i+k₁/2),k₃=hf(x_i+h, y_i+k₂).

Метод Эйлера и его модификация по сути дела являются методами Рунге-Кутта первого и второго порядка соответственно. По сравнению с ними метод Рунге-Кутта обеспечивает более высокую точность, что позволяет увеличить шаг интегрирования h. Допустимая погрешность на шаге определяет его максимальную величину.

Пример 3. Приведём фрагмент программы для решения дифференциального уравнения из примера 1 методом Рунге-Кутта.

Program Runge;

Uses Crt;

Var

xn,xk,yn,h,k0,k1,k2,k3:real;

i,n:integer;

x,y:array [1..20] of real;

Function f(x,y:real):real;

begin

f:=2*x*x+2*y;

end;

Begin

ClrScr;

Writeln(' Решение дифференциального уравнения ');

Writeln(' dy/dx=2x^2+2y методом Рунге-Кутта ');

xn:=0; yn:=1; xk:=1; h:=0.1;

x[1]:=xn; y[1]:=yn; i:=1;

repeat

k0:=h*f(x[i],y[i]);

k1:=h*f(x[i]+h/2,y[i]+k0/2);

k2:=h*f(x[i]+h/2,y[i]+k1/2);

k3:=h*f(x[i]+h,y[i]+k2);

y[i+1]:=y[i]+(k0+2*k1+2*k2+k3)/6;

x[i+1]:=x[i]+h;

i:=i+1;

until x[i]>xk;

n:=i;

Writeln('----------------------');

Writeln('| № | x | y |');

Writeln('----------------------');

for i:= 1 to n do

Writeln('|', i:2, ' |', x[i]:5:2, ' |', y[i]:7:4, ' |');

Writeln('----------------------');

Readln;

End.