1.5. Варианты заданий

№1.1. Найти пределы:

1. ;

2. ;

3. ;

4. ;

5. ;

6. ;

7. ;

8. ;

9. ;

10. ;

11. ;

12. .

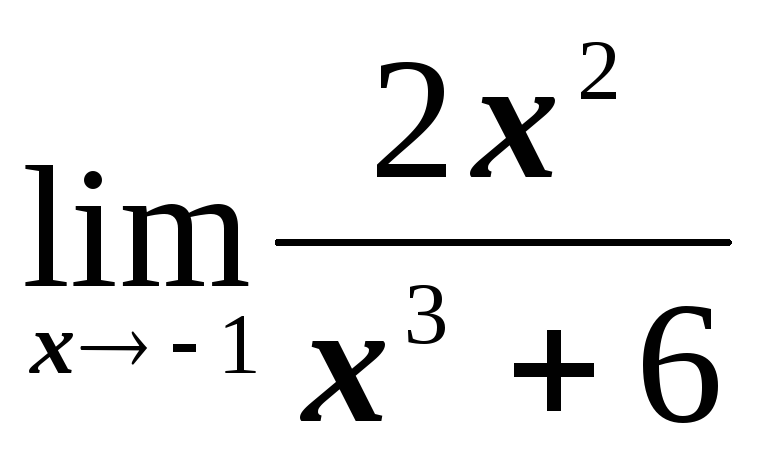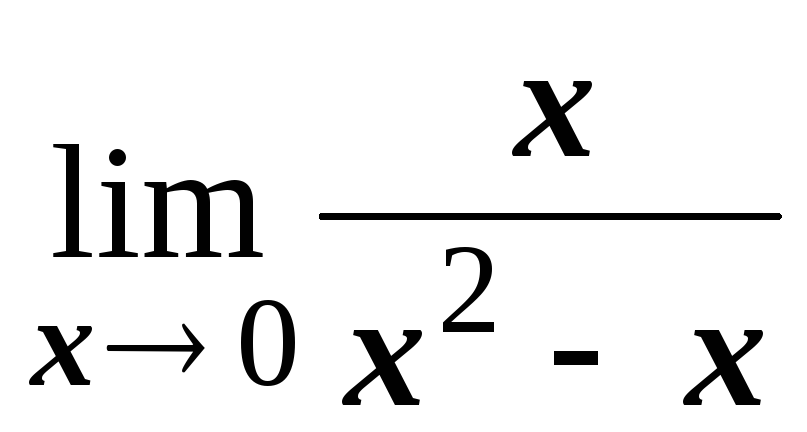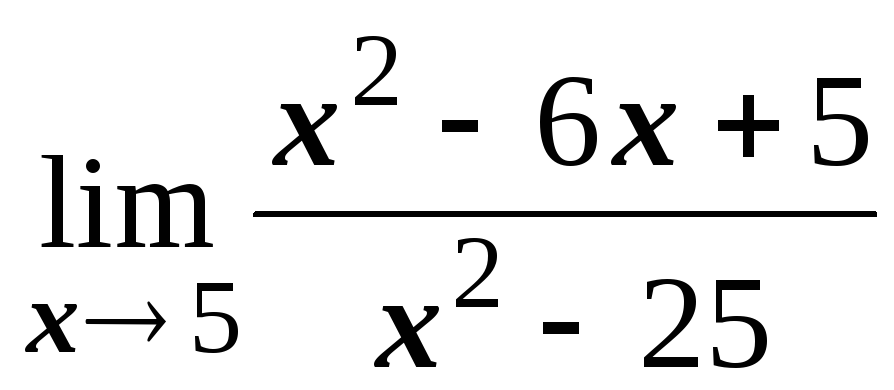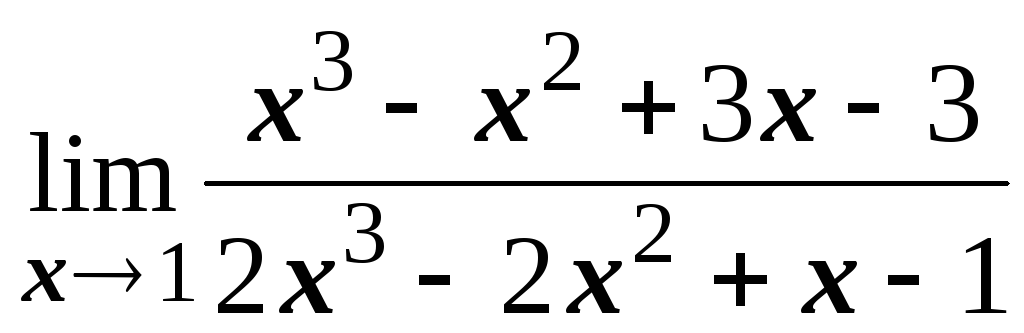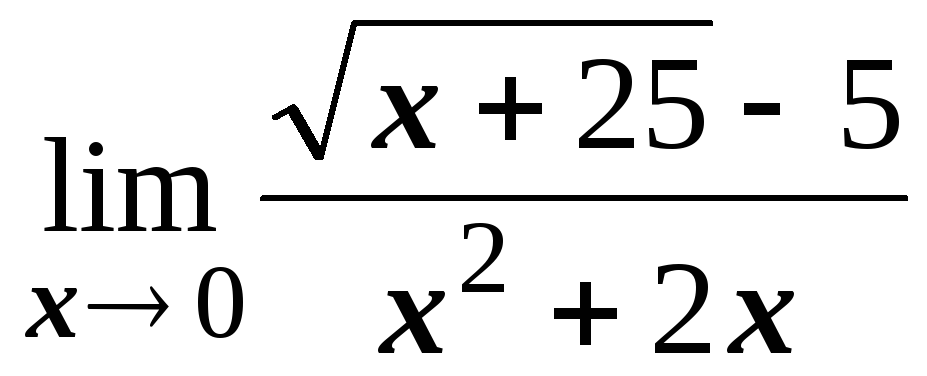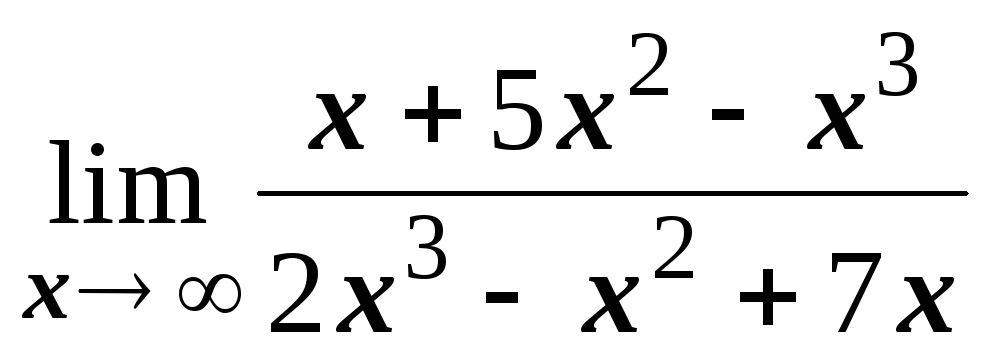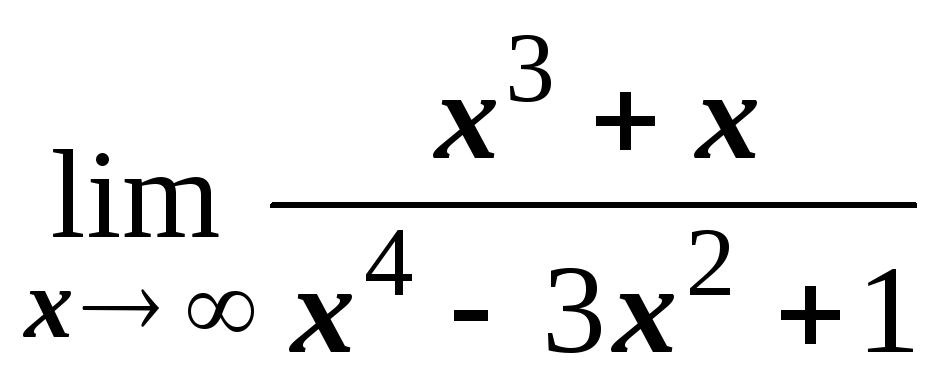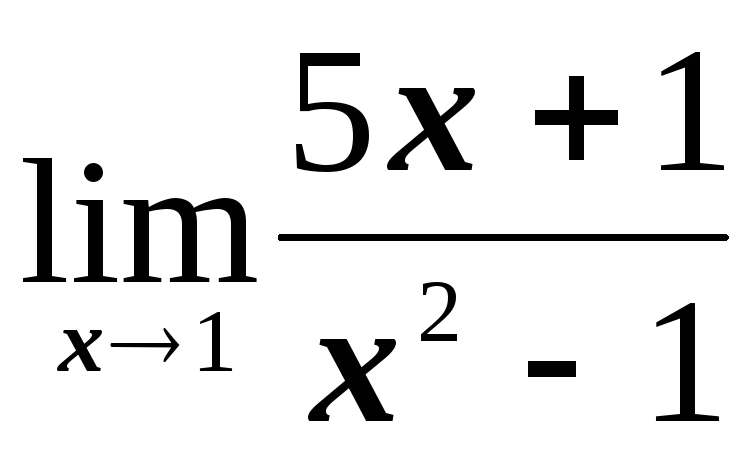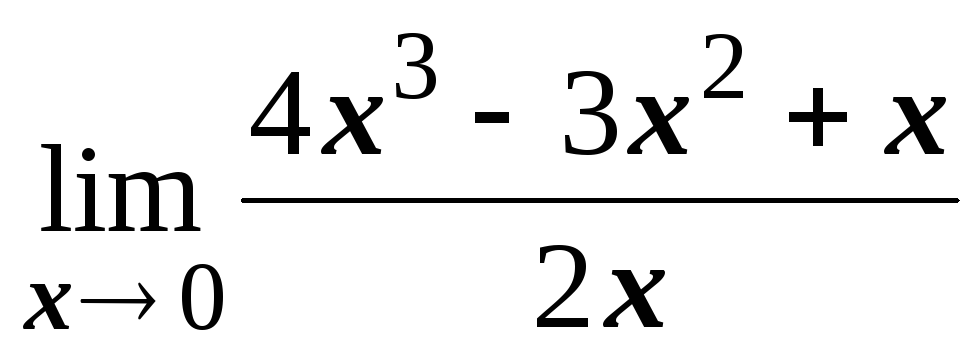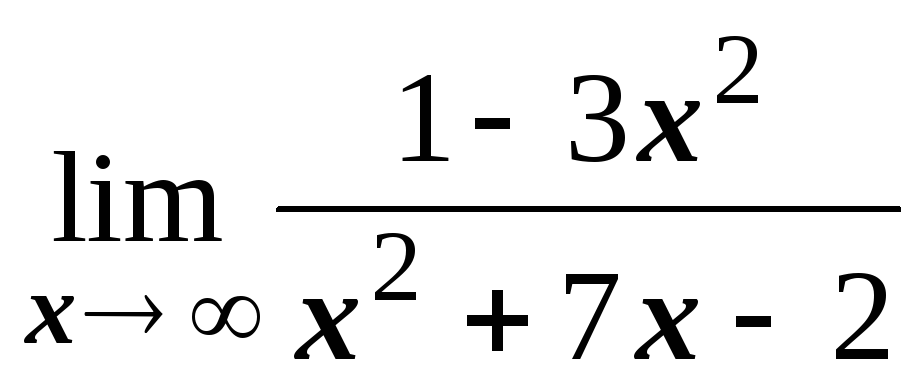№1.2. Найти пределы:

1. ;

2. ;

3. ;

4. ;

5. ;

6. ;

7. ;

8. ;

9. ;

10. .

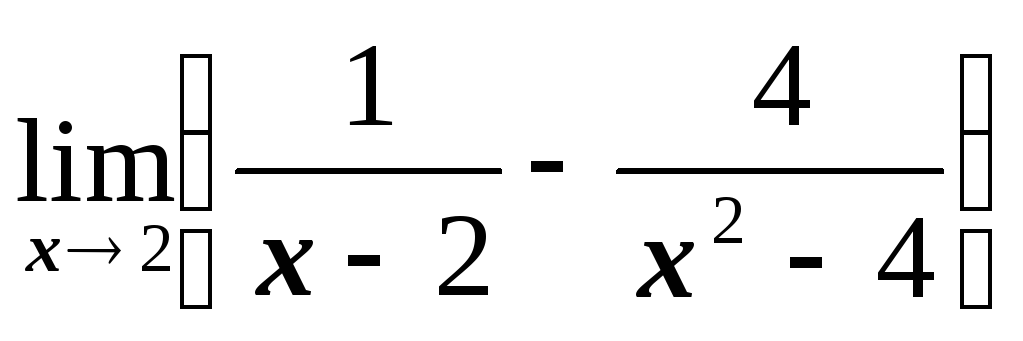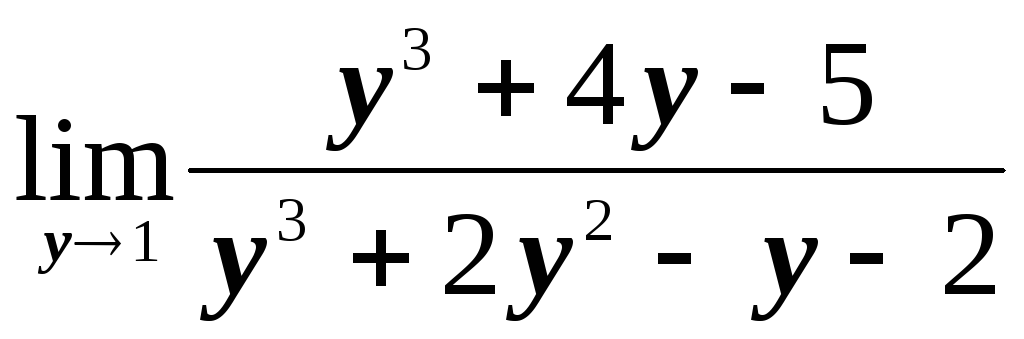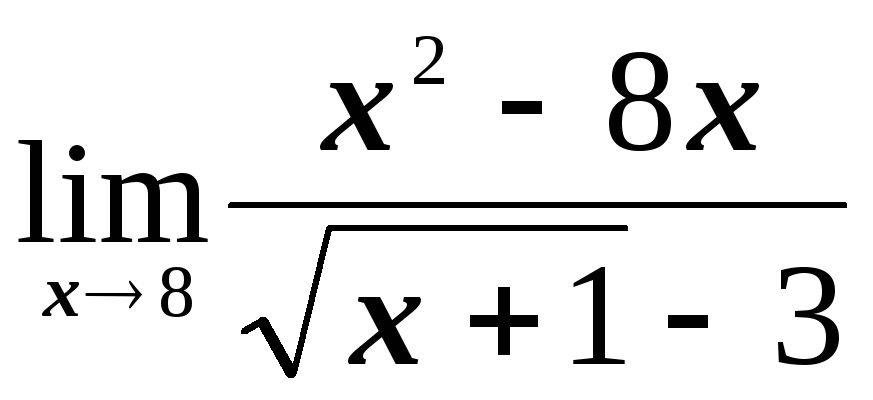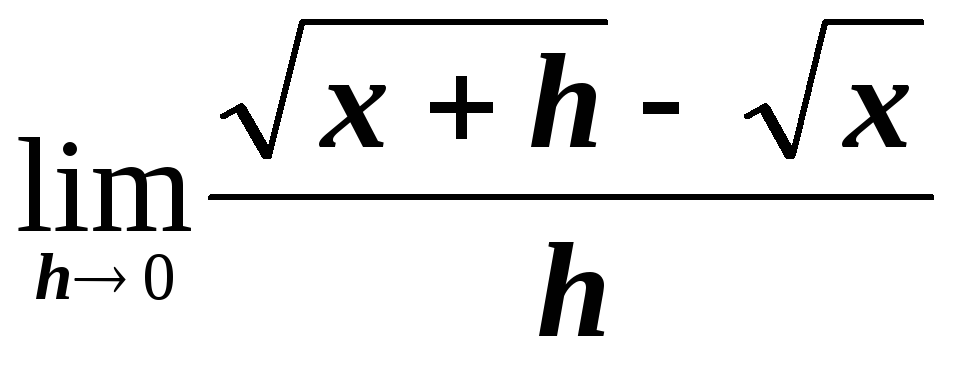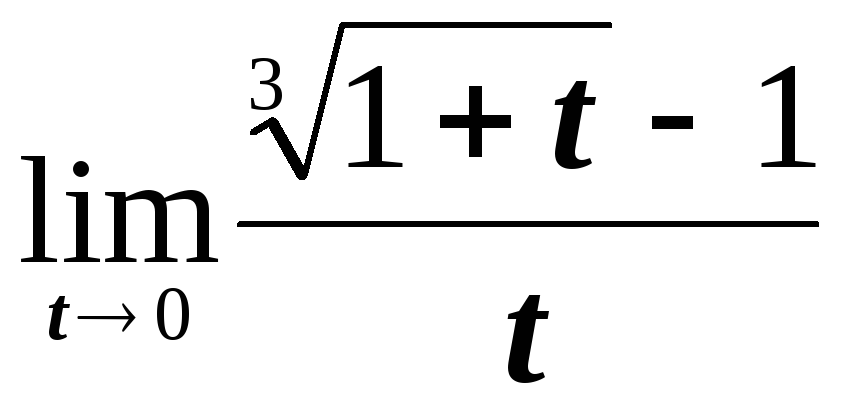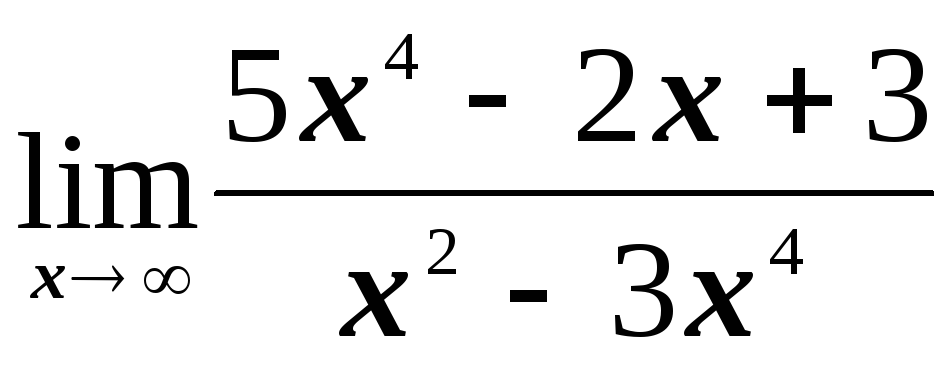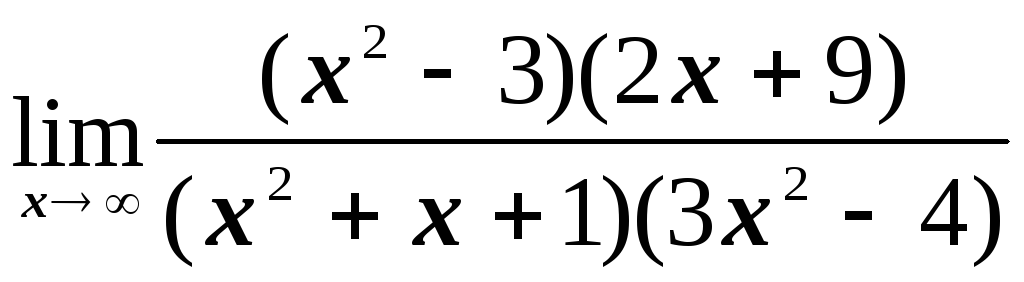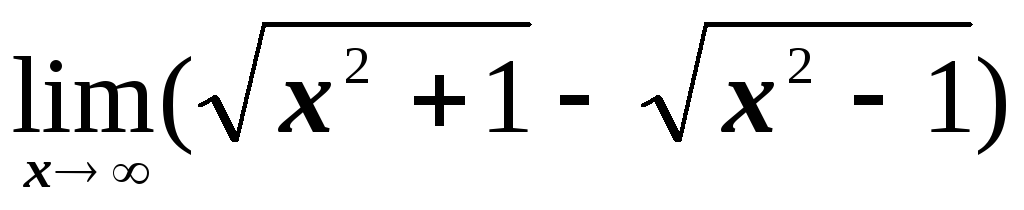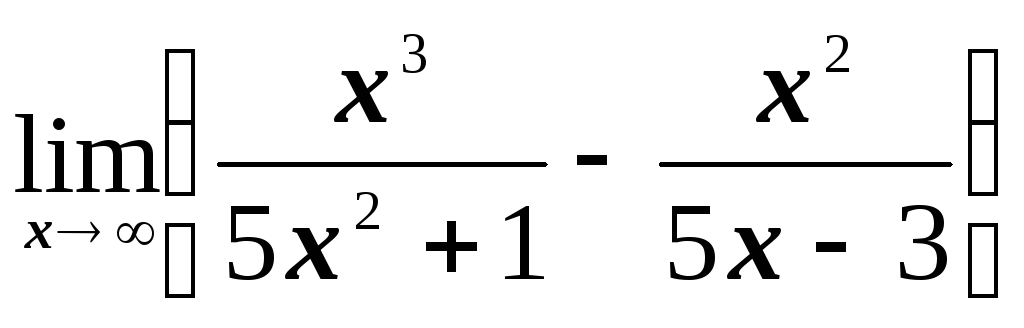№1.3. Найти пределы:

1. ;

2. ;

3. ;

4. ;

5. ;

6. ;

7. ;

8. 

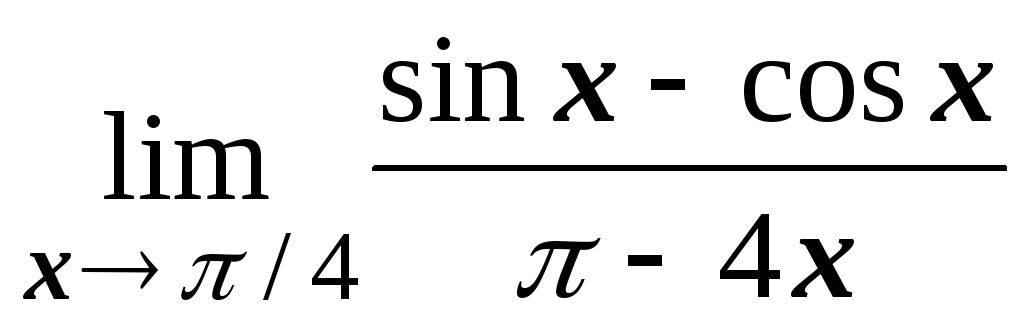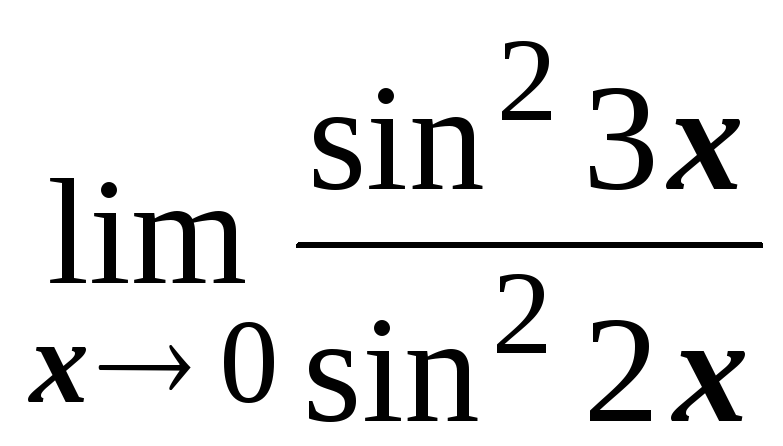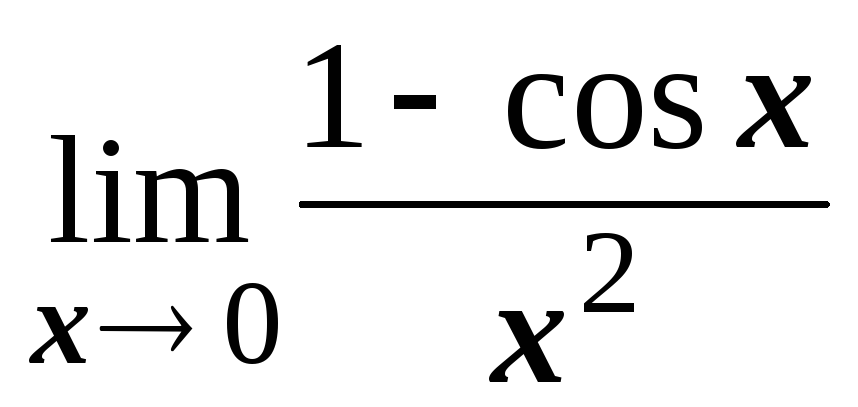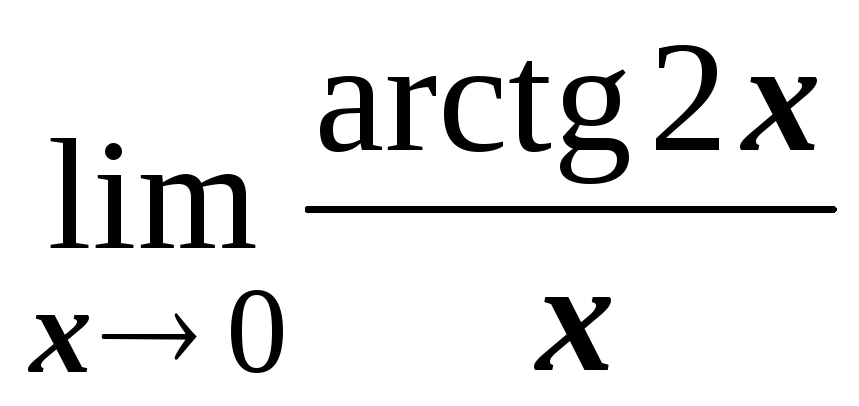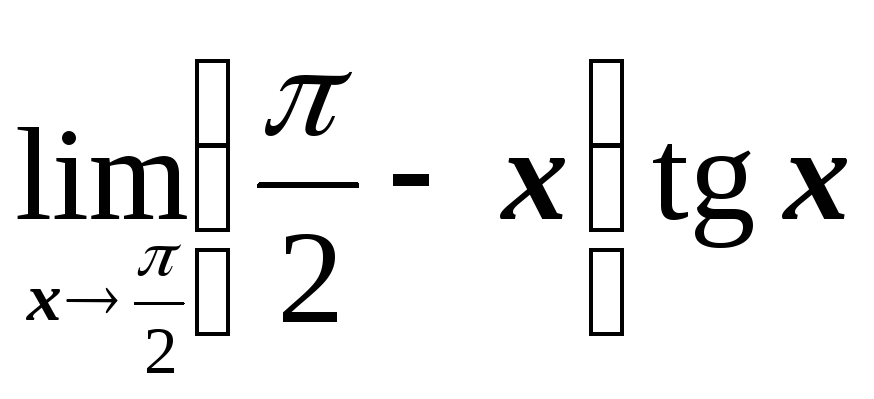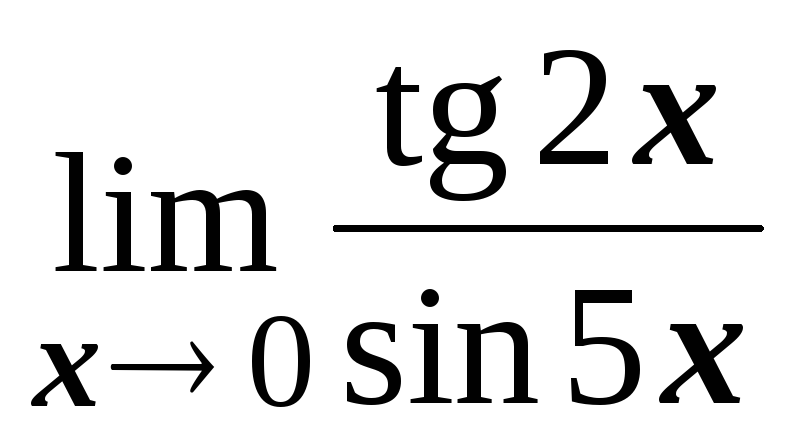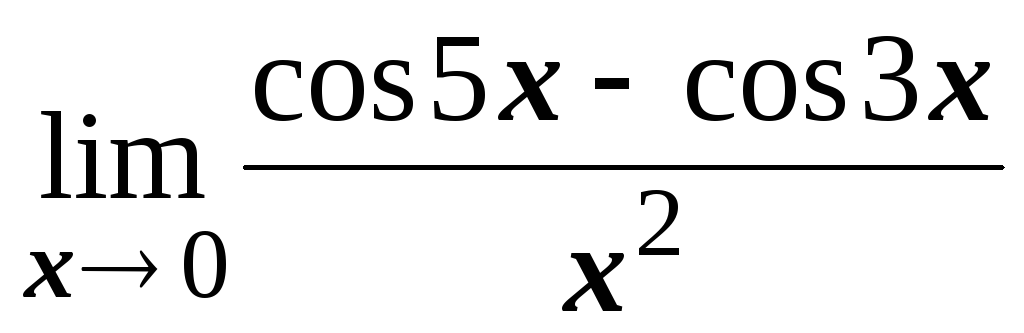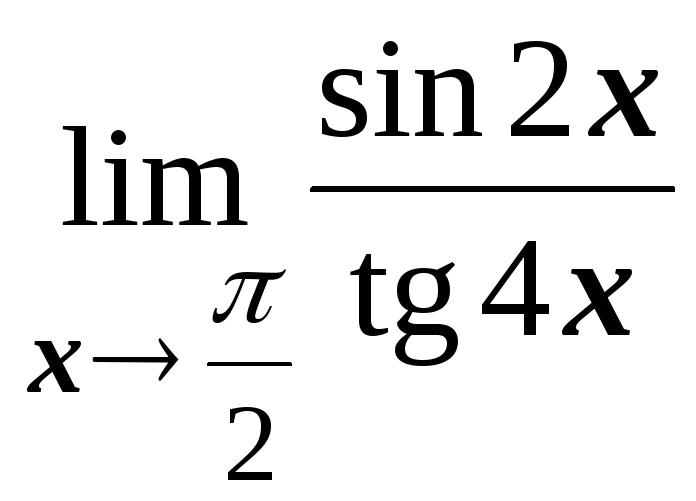
1.6. Контрольные вопросы Глава 2. Производная и дифференциал

2.1 Понятие производной

Рассмотрим функцию y=f(x). Предположим, что x₀ внутренняя точка множества определения функции. Зададим приращение аргумента x0 такое, что точка x₀+xDf. Тогда соответствующее приращение в т. x₀ будет иметь вид: f=f(x₀+x)–f(x₀).

Если существует предел отношения приращения функции к приращению аргумента при условии, что приращение аргумента х0, то он называется значением производной функции f(x) в точке х₀

Обозначение: .

Также возможны и другие обозначения: ,.

Если функция y=f(x) имеет конечную производную в каждой точке некоторого промежутка, то производную можно считать функцией переменной х и обозначать у ^/(х), .

Если в точке x₀ существует конечная производная функции y=f(x), то эта функция называется дифференцируемой в точке x₀.

Если функция y=f(x) дифференцируема в каждой точке некоторого промежутка, то она дифференцируема на промежутке.

2.2. Геометрический и физический смысл производной

Пусть функция y=f(x) имеет производную в точке x₀. Тогда существует касательная к графику этой функции в точке М₀(x₀, у₀), уравнение которой имеет вид

.

При этом , где – угол наклона этой касательной к положительному направлению оси ОХ (рис. 2.1).

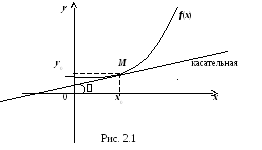
Геометрически, чтобы провести касательную, надо к графику кривой приставить линейку так, чтобы она коснулась графика в выбранной точке.

Геометрический смысл: угловой коэффициент касательной, приведенной к графику функции y=f(x) в точке x₀ равен значению производной функции в этой точке.

Физический смысл: скорость тела равна первой производной координаты по времени:

V(t)=x ^/ (t). (2.1)

Соответственно, вторая производная функции – скорость изменения скорости, т.е. ускорение:

a(t)= V ^/ (t)=x ^// (t). (2.2)

2.3. Таблица производных

1. С  = 0, где С–постоянная

2. (x^m) = mx^m–1

3. 

4. 

5. 

6. 

7. 

8. 

9. 

10. 

11. 

12. 

13. 

14. 

15. 

16. 

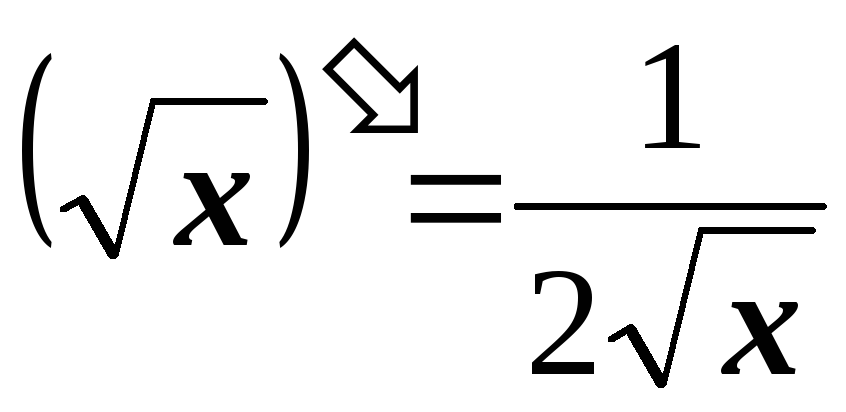
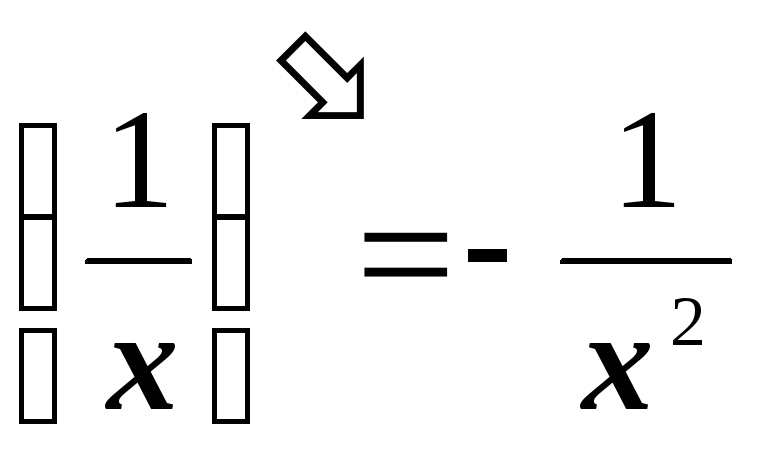
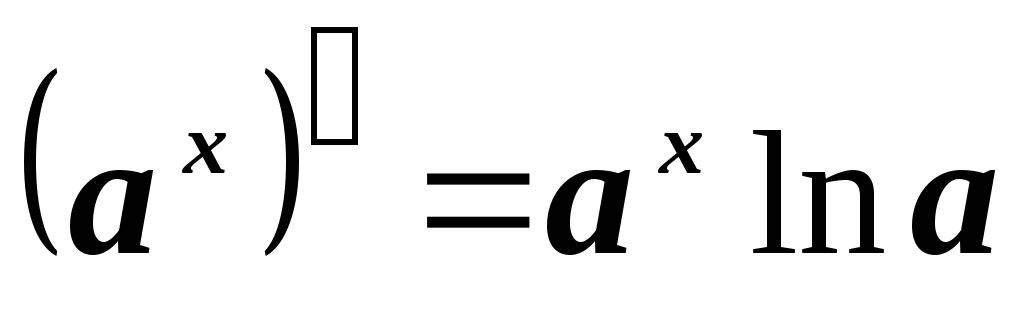
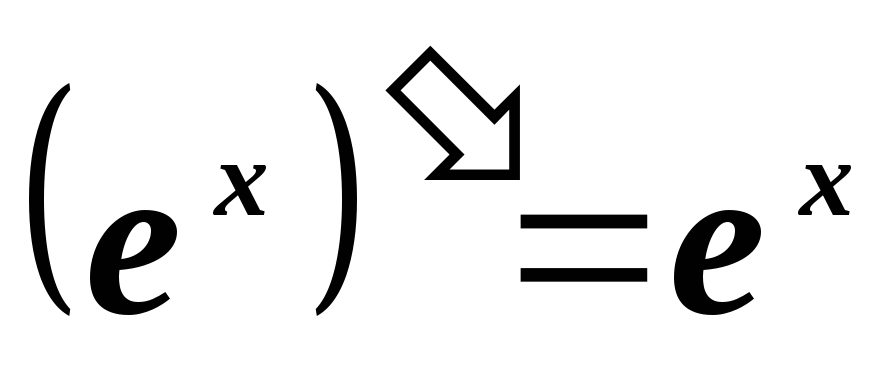
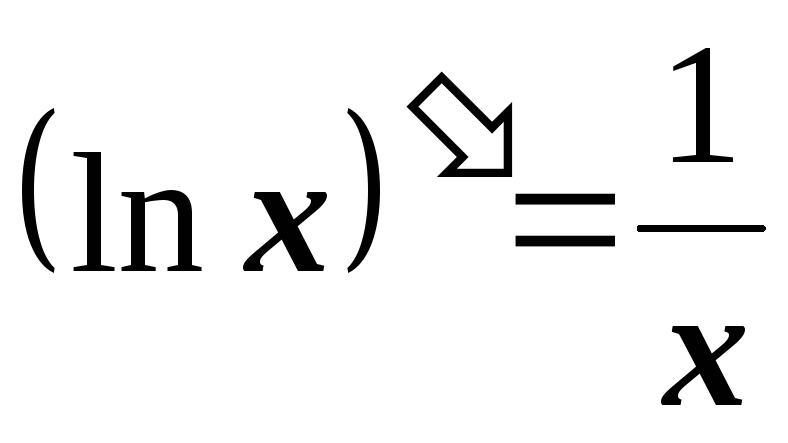
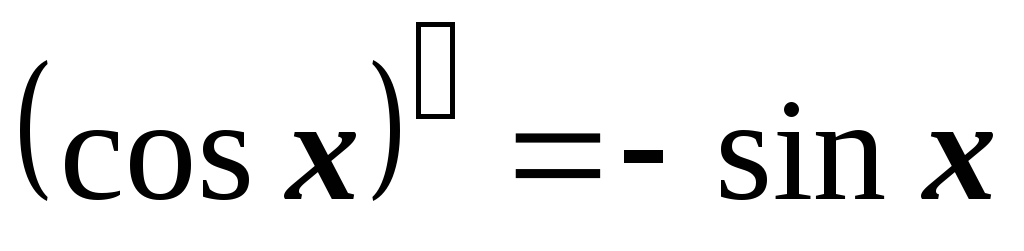
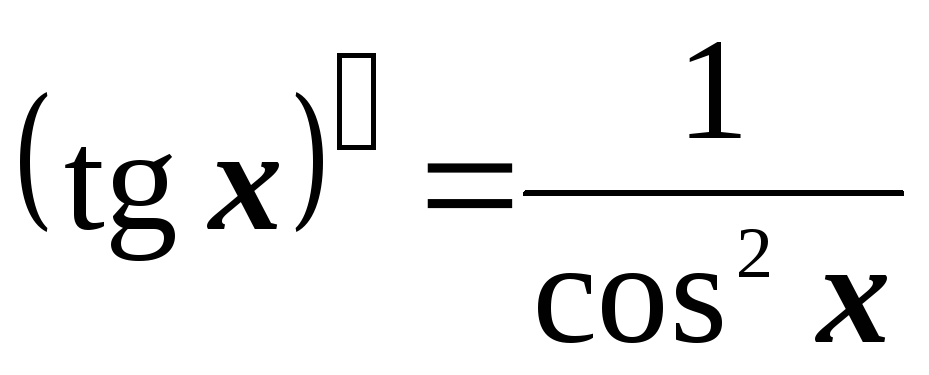
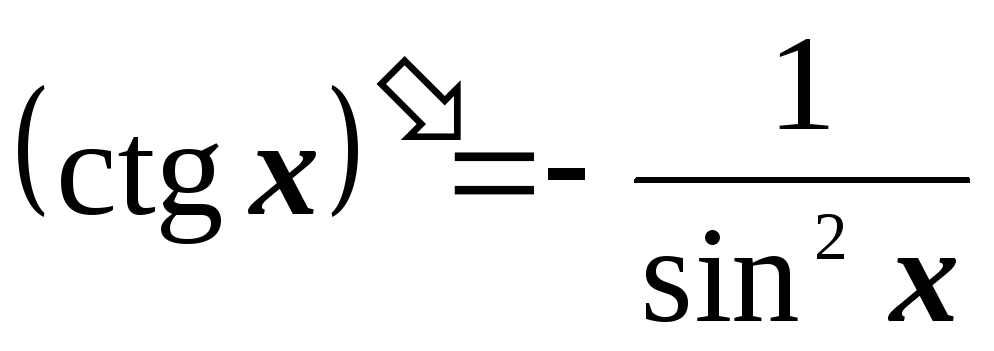
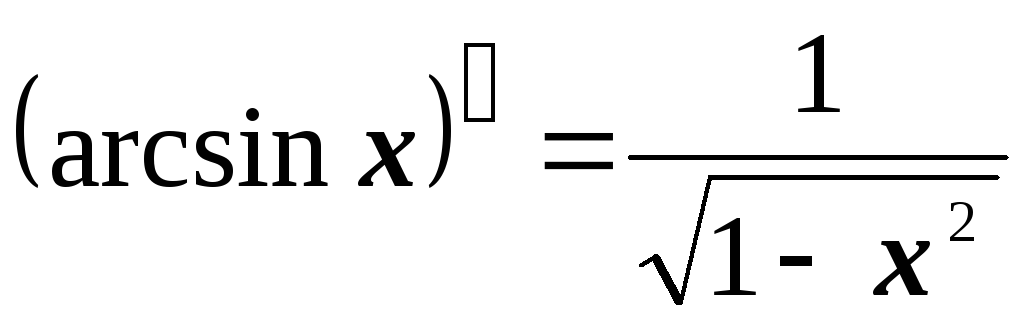
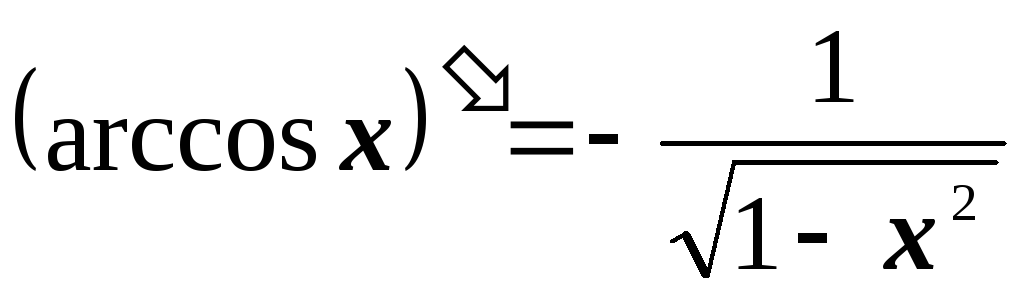
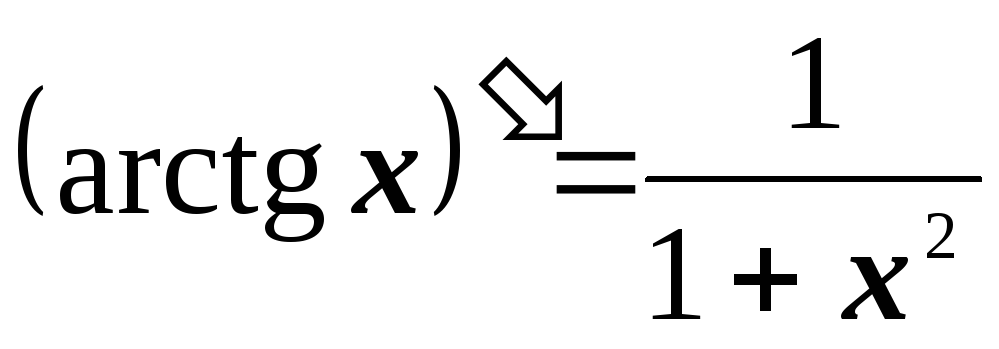
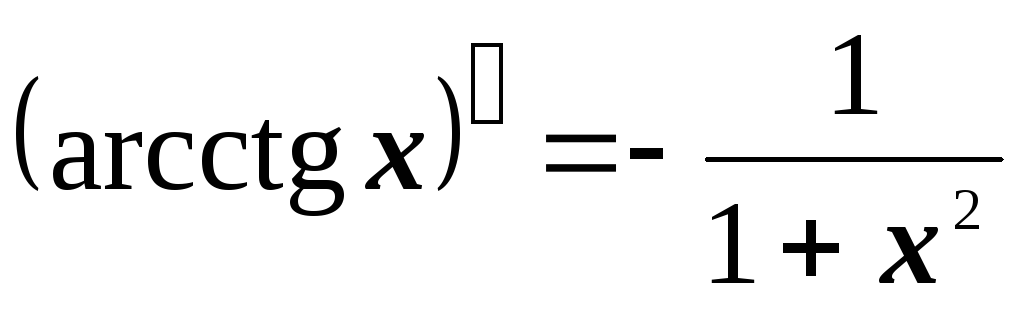
2.4. Основные правила дифференцирования

Пусть u и v – функции, дифференцируемые в точке х. Тогда

1. Производная суммы двух дифференцируемых функций равна сумме их производных:

(u+v) ′=u′+v′

2. Производная произведения двух дифференцируемых функций вычисляется по следующему правилу: (uv) ′=u′v+uv′, в частности (Cu) ′=Cu′, С=const (постоянный множитель можно выносить за знак производной)

3. Производная частного двух дифференцируемых функций вычисляется по следующему правилу:

, где v  0

4. Производная сложной функции равна производной по промежуточному аргументу, умноженной на производную промежуточного аргумента по независимой переменной: y′_x=y′_{u ·} u′_x, где и – промежуточный аргумент.

2.5. Производные высших порядков

Производная f ′ (x) от функции f(x) называется также производной первого порядка. В свою очередь производная от функции f ′ (x) тоже является функцией от x , поэтому также может быть дифференцируема и называется производной второго порядка от функции f(x) (или просто второй производной).

Вторая производная обозначается символами: f′′(х) (читается: «эф два штриха от икс») или («дэ два эф по дэ икс дважды»).

Исходя из определения второй производной, можно записать: .

Аналогично определяется третья производная:

= и т.д.

Производная п-ного порядка обозначается .