3.5. Экономические задачи, сводящиеся к транспортным моделям

В этом параграфе будет рассмотрено несколько примеров экономических задач, оптимальное решение которых может быть найдено с помощью транспортных моделей.

Оптимальное распределение оборудования

Оборудование -различных видов нужно распределить между-рабочими участками. Производительность одной единицы оборудования-го вида на-м рабочем участке равна; ;.Потребность -го участка в оборудовании составляет, .Запас оборудования -ro вида равен , .Найти распределение оборудования на рабочие участки, при котором суммарная производительность максимальная.

Решение.

Данная задача относится к классу транспортных задач при условии, что производительность линейно зависит от количества используемого оборудования. Поставщиками в задаче являются различные виды оборудования, потребителями – рабочие участки. Предложение определяется запасом оборудования каждого вида, спрос – потребностью в нем на рабочем участке.

Обозначим через число единиц оборудования -го вида, выделенное на-й рабочий участок, ;.Математическая модель задачи имеет следующий вид:

Построенная модель является сбалансированной. Если запас оборудования и потребность в нем не равны, то переход к сба­лансированной модели осуществляется с помощью преобразова­ний, изложенных в параграфе 3.2.

В данной задаче требуется максимизировать целевую функцию , представляющую суммарную производительность. Для перехода к стандартной транспортной модели надо заменить функцию на противоположную функцию , которую нужно будет минимизировать.

При решении в транспортной таблице вместо тарифов на перевозки запишутся производительности , взятые с противоположным знаком. Далее задача решается известными методами, представленными в этой главе.

Формирование оптимального штата фирмы

Фирма набирает штат сотрудников. Она располагает группами различных должностей по вакантных единиц в каждой группе, . Кандидаты для занятия должностей проходят тестирование, по результатам которого их разделяют на групп по кандидатов в каждой группе, . Для каждого кандидата из -й группы требуются определенные затраты на обучение для занятия -й должности, ; . (В частности, некоторые =0, т.е. кандидат полностью соответствует должности, или да, т.е. кандидат вообще не может занять данную должность.) Требуется распределить кандидатов на должности, затратив минимальные средства на их обучение.

Решение.

Предположим, что общее число кандидатов соответствует числу вакантных должностей. (Если это не так, то следует просто проделать преобразования параграфа 3.2.). Тогда данная задача соответствует транспортной модели. В роли поставщиков выступают группы кандидатов, а в роли потребителей – группы должностей. Предложением является число кандидатов в каждой группе, спросом – число вакансий в каждой группе должностей. В качестве тарифов на перевозки рассматриваются затраты на переобучение.

Математическая модель записывается в виде

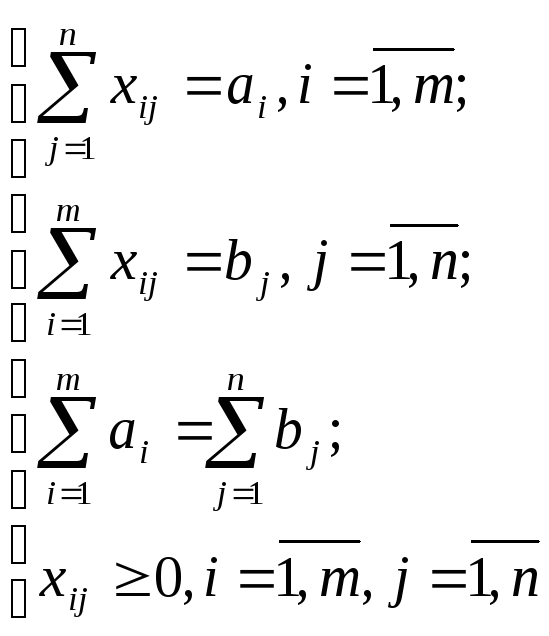
Методы решения этой задачи такие же, как и транспортной задачи.

Задача о назначениях

В общем виде задача о назначениях формулируется следующим образом.

Имеется работ и кандидатов для их выполнения. Затраты -го кандидата на выполнение-й работы равны. Каждый кандидат может быть назначен только на одну работу, и каждая работа может быть выполнена только одним кандидатом. Требуется найти назначение кандидатов на работы,при котором суммарные затраты на выполнение работ минимальны.

Запишем формально данную задачу. Пусть – переменная, значение которой равно 1, если -й кандидат выполняет-ю работу, и 0 – в противном случае. Тогда условие о том, что каждый кандидат выполняет только одну работу, запишется в виде

Условие о том, что каждая работа может выполняться одним кандидатом, запишется в виде

Целевая функция задачи имеет вид

В функцию входят только те значения (; ), для которых отличны от 0, т.е. входят затраты, соответствующие назначенным работам.

Математическая модель выглядит следующим образом:

(3.5.1)

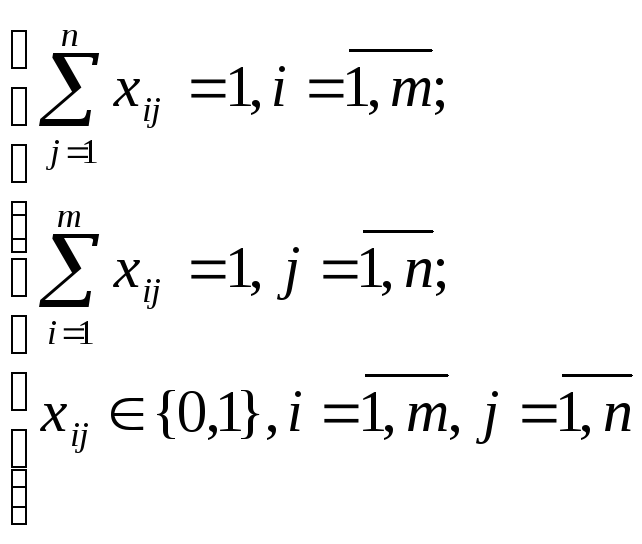(3.5.2)(3.5.3)(3.5.4)

Решить задачу о назначениях – значит найти , удовлетворяющие (3.5.2) – (3.5.4) и доставляющие минимум функции (3.5.1). Задача (3.5.1) – (3.5.4) является, очевидно, задачей линейного программирования (целевая функция линейна, ограничения линейны) и может быть решена симплекс-методом. Также задача (3.5.1) – (3.5.4) – это транспортная задача, в которой правые части ограничений равны 1, а переменные могут принимать только два значения. Однако относительно простая форма задачи позволила разработать для ее решения достаточно простые методы, один из которых – венгерский.