4.3. Метод множителей Лагранжа

Пусть требуется решить задачу нелинейного программирования следующего вида:

(4.3.1)

(4.3.2)

где функции и , непрерывны, и непрерывны их част­ные производные по , .

Для решения поставленной задачи может быть применен метод множителей Лагранжа. Объясним идею метода на примере ЗНП, зависящей от двух переменных.

На плоскости уравнение определяет график некоторой функции, представленный на рис. 4.3.1. На нем показаны несколько линий уровня некоторой функции и выбранное в качестве примера направление ее возрастания.

Рис. 4.3.1

В точке А, в которой функция достигает максимального значения, совпадают касательные линии к графикам функций

и .

Следовательно, в точке А векторы-нормали к функциям и пропорциональны. Обозначим эти векторы соответственно через и .Получаем

,

где – некоторый коэффициент пропорциональности. Координатами векторов иявляются значения частных производных функций и соответственно в точке А.

;

.

Из условия пропорциональности в точке А имеем

;

.

Для определения значений , в которых функция достигает максимума, к этим уравнениям надо добавить условие принадлежности точкиА графику функции .

Окончательно получаем систему уравнений, определяющую оптимальное решение поставленной задачи

Введем новую функцию

.

Тогда последняя система перепишется в виде

Функцию называют функцией Лагранжа.

Алгоритм метода множителей Лагранжа решения задачи (4.3.1), (4.3.2)

Шаг 1. Составляют функцию Лагранжа

Шаг 2. Находят частные производные функции Лагранжа по и , , и приравнивают их к нулю

Шаг 3. Решают систему (4.3.3) и определяют точки, в которых функция может иметь экстремум.

Шаг 4. Проверяют полученные на шаге 3 точки на экстремум и определяют экстремальное значение функции в найденной точке.

4.4. Расчет экономико-математической модели при нелинейных затратах на производство

Рассмотрим применение изученных методов на примере решения задачи оптимальной реализации продукции.

Пример 4.4.1

Фирма реализует автомобили двумя способами: через магазин и через торговых агентов. При реализации автомобилей через магазин расходы на реализацию составляют усл. ед., а при продаже автомобилей через торговых агентов расходы составляют усл. ед. Найти оптимальный способ реализации автомобилей, минимизирующий суммарные расходы, если общее число предназначенных для продажи автомобилей составляет 200 штук.

Решение.

Составим математическую модель задачи.

Целью является минимизация суммарных расходов

.

Управляющие переменные – это число автомобилей, реализуемых первым и вторым способом: и соответственно (200 штук). Окончательно математическая модель имеет следующий вид:

.

.

Для ее расчета применим метод множителей Лагранжа. Функция Лагранжа имеет вид

.

Найдем частные производные функции по , и и приравняем их к нулю.

Получим следующую систему уравнений:

.

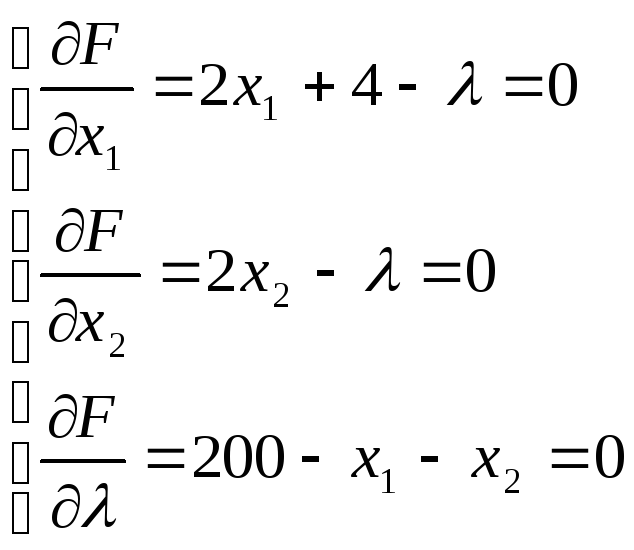Решая систему, найдем

=99, =101, =202,=20398.

Определитель, составленный из вторых частных производных функций по,, имеет вид

Следовательно, по теореме о достаточном условии существования условного экстремума функция в точке =99,=101 действительно имеет экстремум.

следовательно в этой точке функция имеет условный минимум.

Таким образом, для получения минимальных расходов, нужно реализовать 99 автомобилей через магазин и 101 автомобиль через торговых агентов. При этом расходы на реализацию составят 20398 усл. ед.

Данную задачу можно было решить и графическим методом (рис. 4.4.1).

Рис. 4.4.1

Областью допустимых решений задачи является отрезок АВ, линиями уровня функции являются концентрические окружности с центром в точке =-2,=0 и радиусом .

Из рисунка видно, что минимальное значение функции, принадлежащее области допустимых решений, достигается в точке , в которой совпадают угловой коэффициент прямой =200-и касательной к окружности к оси .

Продифференцировав последнее уравнение по , получим

,

.

Приравняем последнее выражение к угловому коэффициенту прямой и добавим к этому уравнению уравнение прямой, которой принадлежит точка Е.

Решив последнюю систему, найдем оптимальные значения: =99,=101, =20398.