
3. Нахождение собственных векторов
Для нахождения собственных векторов преобразуем равенство (8)
АХ = λХ,
перепишем его в виде
АХ − λХ = 0, или АХ − λЕХ = 0
(А − λЕ)Х = 0. (9)
Здесь 0 – нулевая
матрица. Перейдя к координатной форме,
получим однородную
систему
линейных уравнений. В случае
![]() ,
где
,
где![]() – собственные значения, её главный
определитель равен нулю (
– собственные значения, её главный
определитель равен нулю (![]() ).
Поэтому эта система обязательно имеет
ненулевые (нетривиальные) решения, так
как равный нулю определитель имеет
пропорциональные строки, и
).
Поэтому эта система обязательно имеет
ненулевые (нетривиальные) решения, так
как равный нулю определитель имеет
пропорциональные строки, и
![]() :
:
 (10)
(10)
Подставляя
поочерёдно значения
![]() ,
полученные из характеристического
уравнения, в уравнения системы (10), найдемn
собственных
векторов. Собственный вектор можно
определить с точностью до постоянного
множителя.
,
полученные из характеристического
уравнения, в уравнения системы (10), найдемn
собственных
векторов. Собственный вектор можно
определить с точностью до постоянного
множителя.
3.1. Случай
Матричное уравнение (А − λЕ)Х = 0 имеет развёрнутую форму:
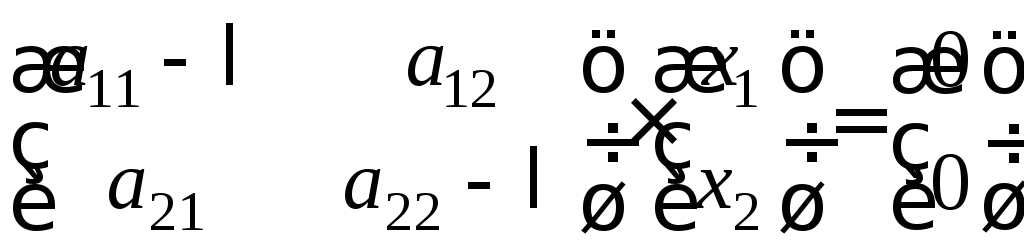 . (11)
. (11)
Восстановим систему уравнений:
 (12)
(12)
Это линейная
однородная система. При
![]() и
и![]() её главный определитель равен нулю.
Поскольку частные определители содержат
нулевые столбцы, они также равны нулю.
По теореме Крамера эта система имеет
бесчисленное множество решений. Ранг
матрицыА −
λЕ
равен
единице, и одно уравнение пропорционально
другому, т.е. оно является лишним.
её главный определитель равен нулю.
Поскольку частные определители содержат
нулевые столбцы, они также равны нулю.
По теореме Крамера эта система имеет
бесчисленное множество решений. Ранг
матрицыА −
λЕ
равен
единице, и одно уравнение пропорционально
другому, т.е. оно является лишним.
Пример 1.
Найти собственные значения и собственные
векторы линейного преобразования с
матрицей
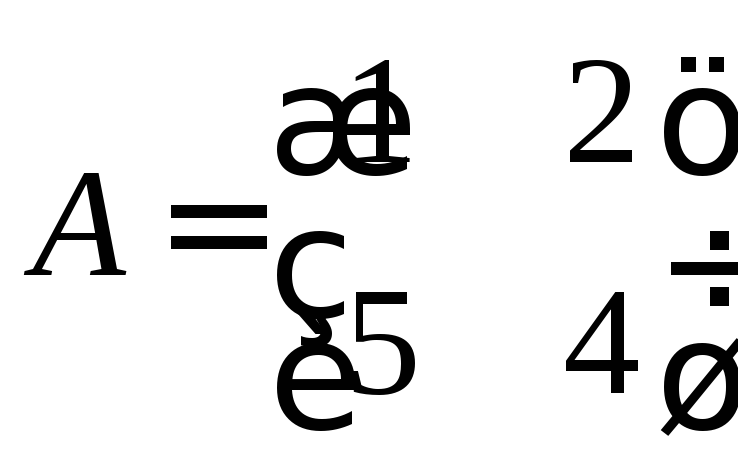 .
.
Решение. Составим характеристическое уравнение:
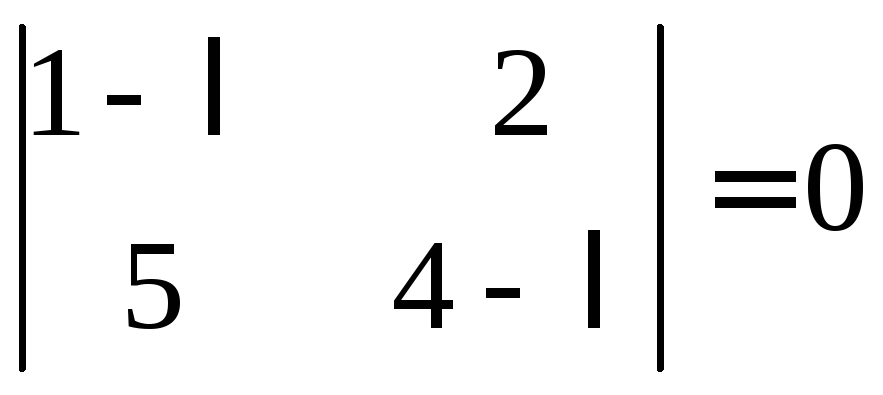 .
.
Найдём собственные
значения λ, решая уравнение
![]() .
Его корни λ1
= 6, λ2
= –1. Это собственные значения матрицы
А.
Собственные векторы находятся из двух
систем уравнений
.
Его корни λ1
= 6, λ2
= –1. Это собственные значения матрицы
А.
Собственные векторы находятся из двух
систем уравнений
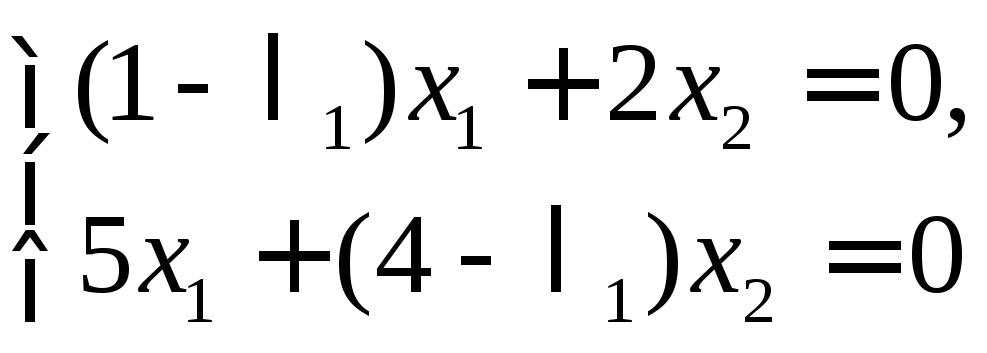 и
и
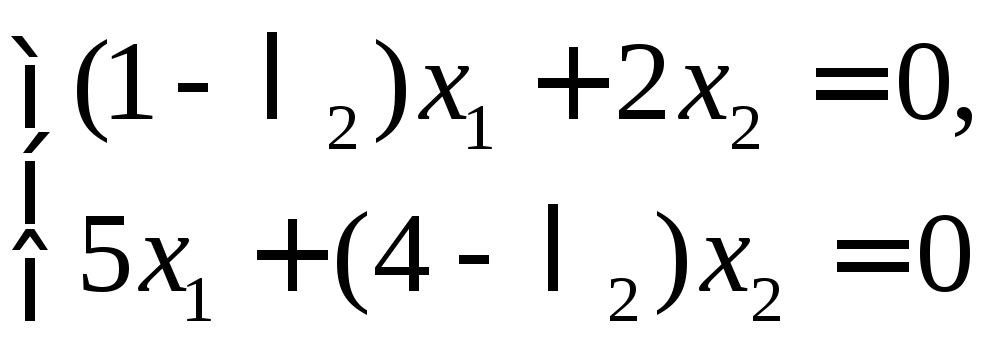 .
.
Главный определитель каждой из этих систем равен нулю. Поэтому каждая из этих однородных систем сводится к одному уравнению.
1) При λ1
= 6 имеем систему
 ,
которая сводится к уравнению
,
которая сводится к уравнению![]() .
Из уравнения следует:
.
Из уравнения следует: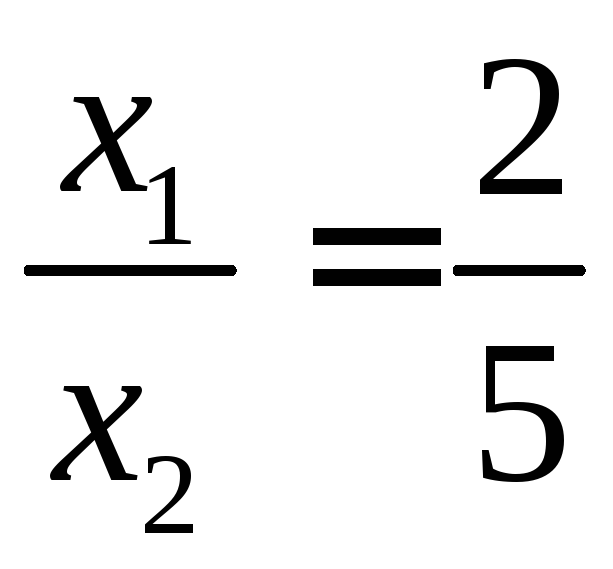 ,
или
,
или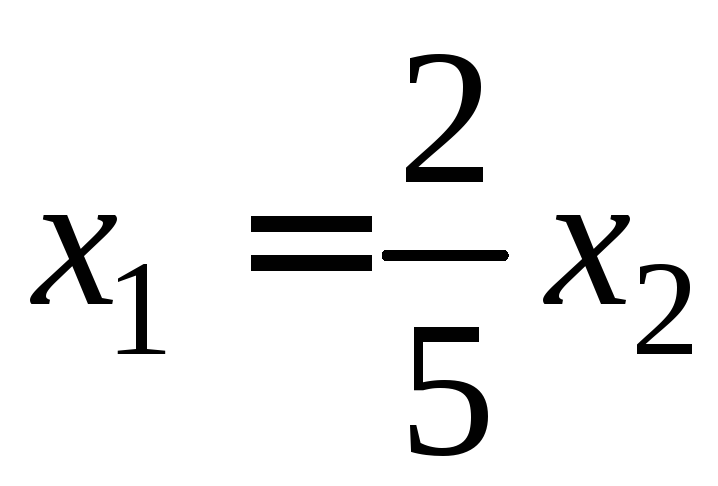 .
В качестве собственного вектора,
соответствующего собственному значению
λ1
= 6, можно взять вектор
.
В качестве собственного вектора,
соответствующего собственному значению
λ1
= 6, можно взять вектор
 .
Подойдёт также любой вектор, кратныйХ1,
например,
.
Подойдёт также любой вектор, кратныйХ1,
например,
![]() или
или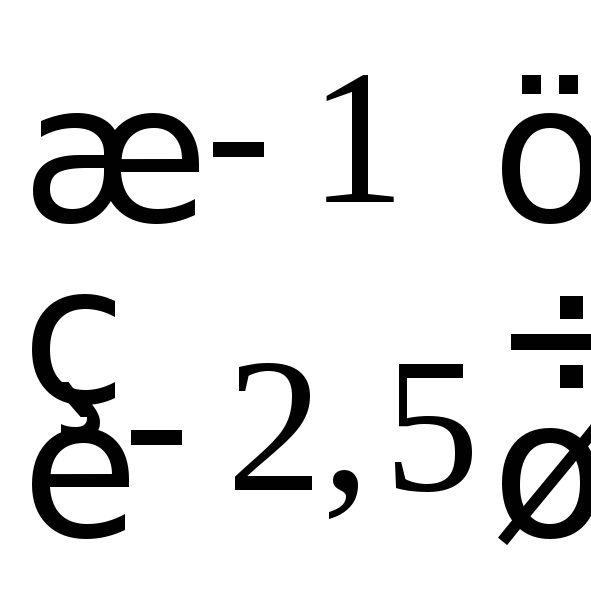 .
.
2) При λ2
= –1 система имеет вид
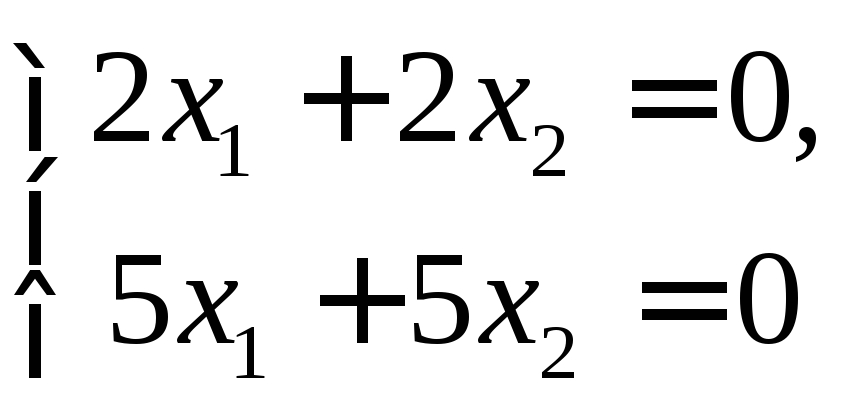 ,
она приводится к одному уравнению
,
она приводится к одному уравнению![]() и
и .
Собственный вектор, соответствующий
данному собственному значениюλ2
= –1,
.
Собственный вектор, соответствующий
данному собственному значениюλ2
= –1,
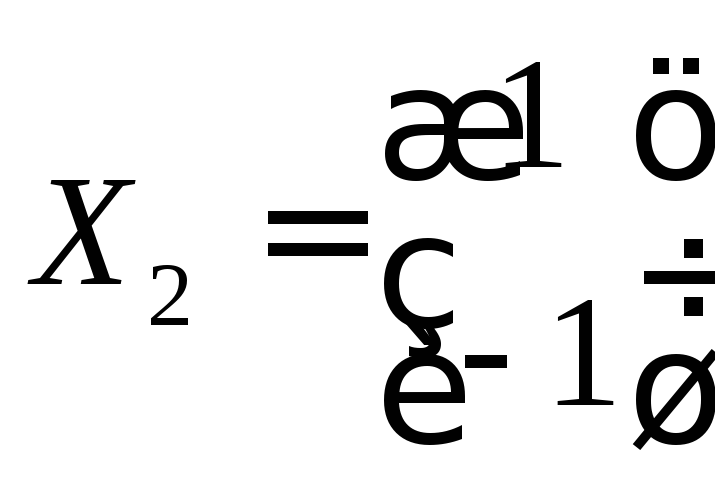 (или любой вектор, кратный ему).
(или любой вектор, кратный ему).
Ответ:
![]() ,
,![]() ,
,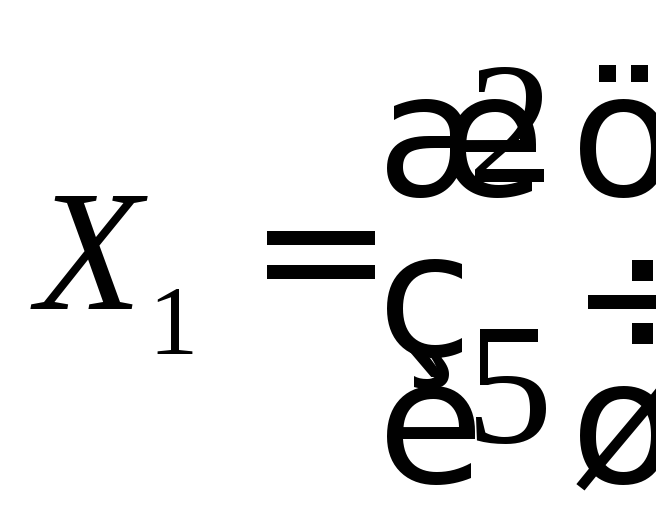 ,
,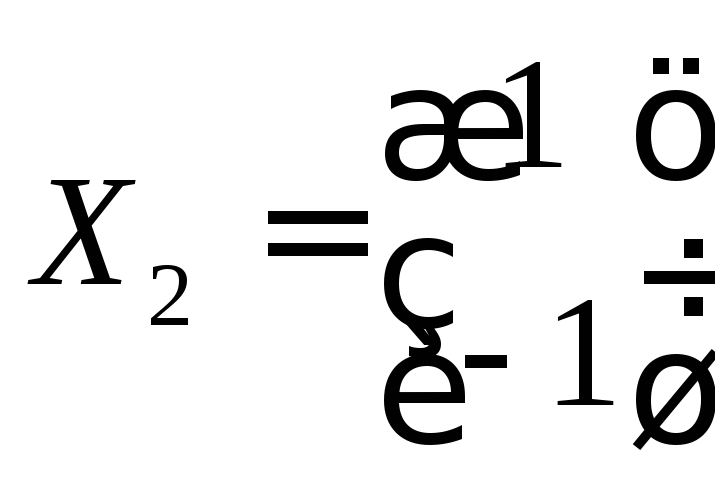 .
.
3.1. Случай
Пример 2.
Найти собственные значения и собственные
векторы линейного преобразования с
матрицей
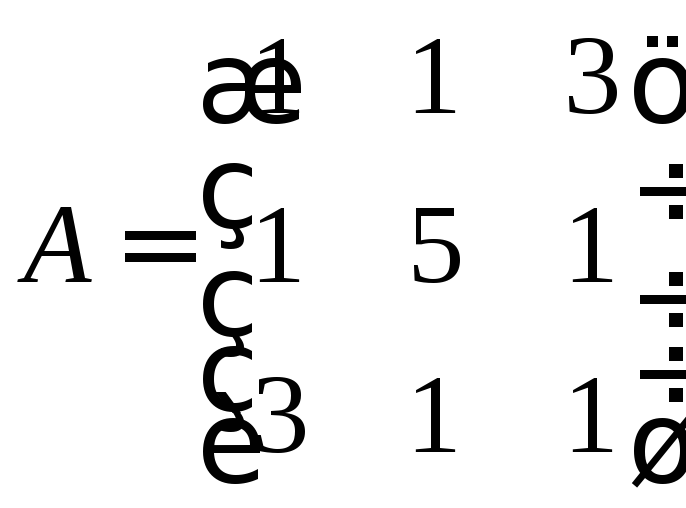 .
.
Решение. Составим характеристическое уравнение
 .
.
Разложим определитель по элементам первой строки:

![]() .
.
Раскрыв скобки и приведя подобные члены, получим уравнение третьей степени:
![]() ;
;
![]()
![]()
![]()
![]()
![]() .
.
Чтобы решить это
уравнение, поступим следующим образом.
Методом подбора найдём один из корней
уравнения λ1,
которым может быть один из делителей
свободного члена. Нетрудно убедиться
в том, что λ1
= 3 есть корень уравнения. Это значит,
что левая часть уравнения делится без
остатка на разность (λ − 3), т. е.
![]() .
.
Определим два
других корня из уравнения
![]() .
По теореме Виета получим следующие два
корня: λ2
= 6, λ3
= –2. Для нахождения собственных векторов
нужно решить три системы уравнений,
последовательно подставляя полученные
собственные значения.
.
По теореме Виета получим следующие два
корня: λ2
= 6, λ3
= –2. Для нахождения собственных векторов
нужно решить три системы уравнений,
последовательно подставляя полученные
собственные значения.
1) При λ1 = 3 имеем однородную систему уравнений
 или
или
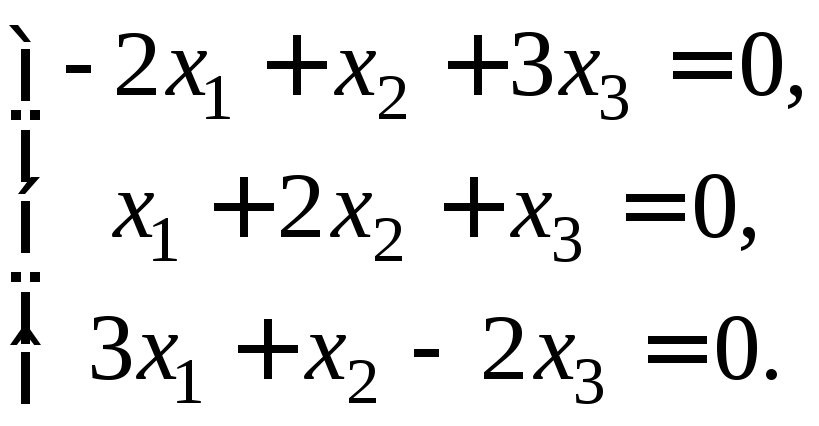
Для решения системы составим матрицу из коэффициентов системы и с помощью элементарных преобразований приведем ее к следующему виду
 ~
~
 ~
~ .
.
Поскольку две последние строки пропорциональны, одну из них можно удалить, тогда исходная система примет вид:
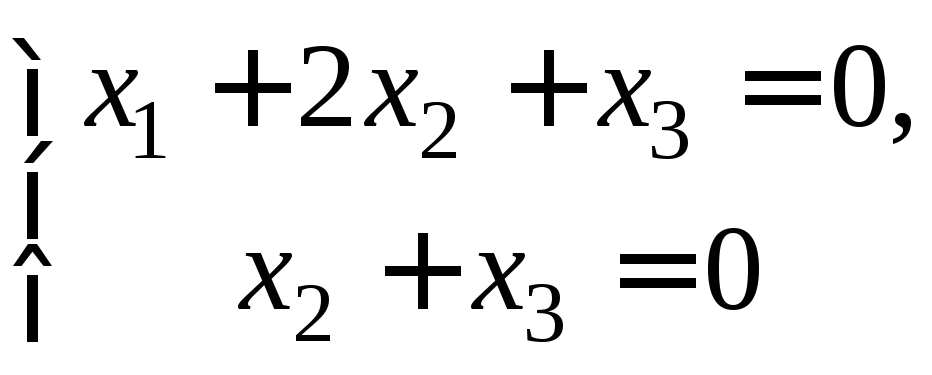 .
.
Решая эту систему,
находим
![]() .
Положим
.
Положим![]() ,
тогда получим собственный вектор
,
тогда получим собственный вектор ,
соответствующий собственному значению
λ1=3.
,
соответствующий собственному значению
λ1=3.
2) При λ2 = 6 имеем систему уравнений
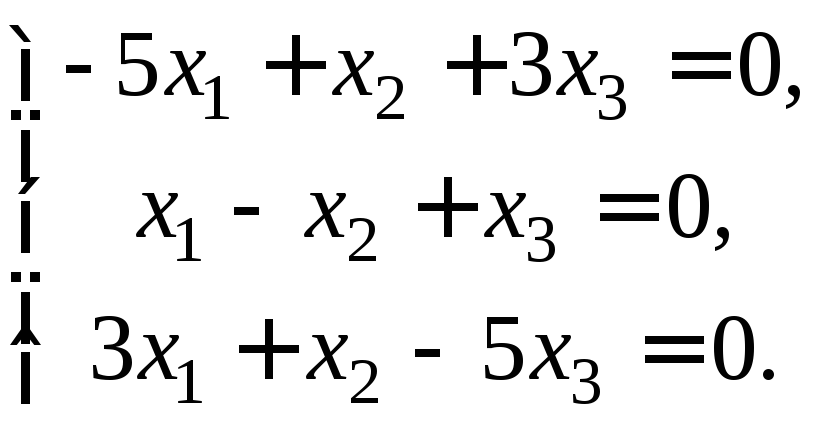 .
.
Составим матрицу из коэффициентов системы и с помощью элементарных преобразований приведем её к следующему виду
 ~
~
 ~
~ .
.
Последнюю строку матрицы можно удалить, а вторую строку разделить на (–4), тогда придём к системе двух уравнений с тремя неизвестными, одно из которых может быть выбрано произвольно:
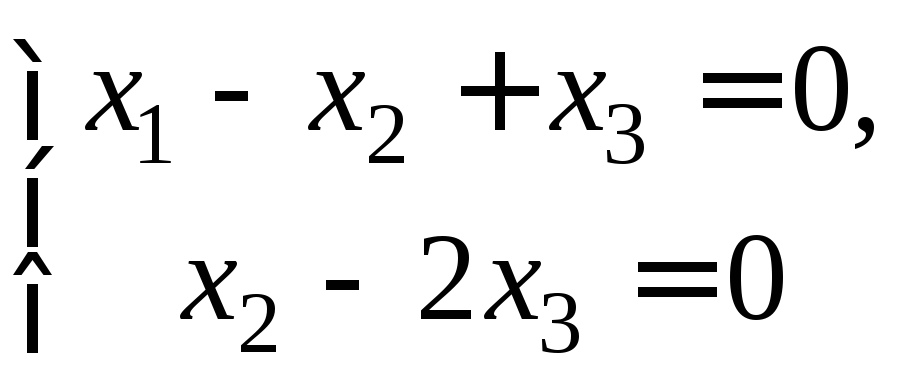 .
.
Пусть
![]() ,
тогда
,
тогда![]() ,
,![]() .
Собственный вектор
.
Собственный вектор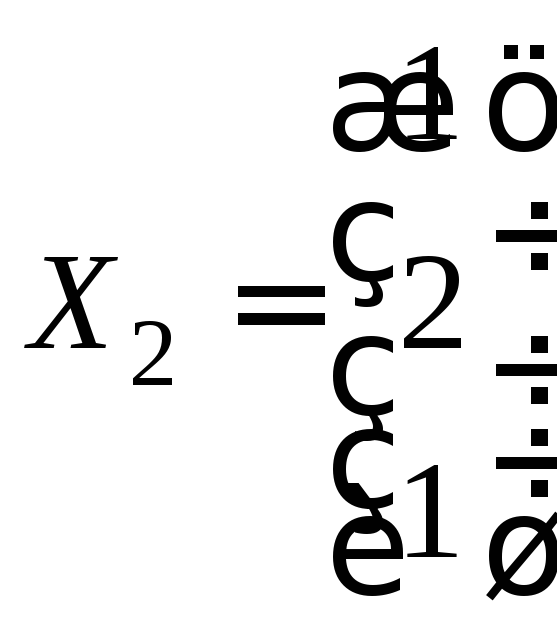 .
.
3) Точно так же
находим собственный вектор
 ,
соответствующий собственному значению
λ3
= –2.
,
соответствующий собственному значению
λ3
= –2.
Следует заметить, что матрица преобразования А в данном примере является симметрической, так как её элементы, расположенные над главной и под главной диагональю, одинаковы. В этом случае, в чём легко убедиться, собственные векторы взаимно ортогональны:
![]() ,
,
![]() ,
,
![]() .
.
Ответ: λ1
= 3, λ2
= 6, λ3
= –2,
 ,
,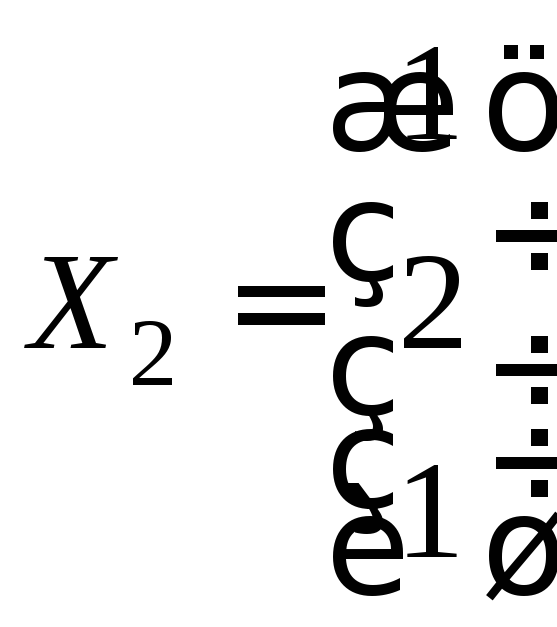 ,
, .
.
