10.3. Дифференциал функции нескольких переменных

Полным приращением функциив точке, соответствующим приращениям аргументов, называется:

.

Функция называетсядифференцируемой в точке , если в некоторой окрестности этой точки полное приращение функции может быть представлено в виде

,

где ,– числа,– бесконечно малая более высокого порядка, чем.

Дифференциалом 1-го порядка функциив точкеназывается главная часть полного приращения функции, линейная относительно приращений аргументов, т.е.

.

Для дифференциала 1-го порядка функции справедлива следующая формула:

. (10.1)

При достаточно малом для дифференцируемой функциисправедливы следующие приближенные равенства:

; . (10.2)

Дифференциалом 2-го порядка функцииназывается дифференциал от ее дифференциала. Аналогично определяются дифференциалы более высоких порядков. Дифференциал порядкаm символически выражается формулой

,

которая раскрывается по биномиальному закону. Например, для функции двух переменных дифференциал 2-го порядка вычисляется по формуле:

. (10.3)

Пример 5. Найти дифференциалы 1-го и 2-го порядков функции и проверить равенство.

Решение. Найдем частные производные 1-го порядка этой функции:

;

.

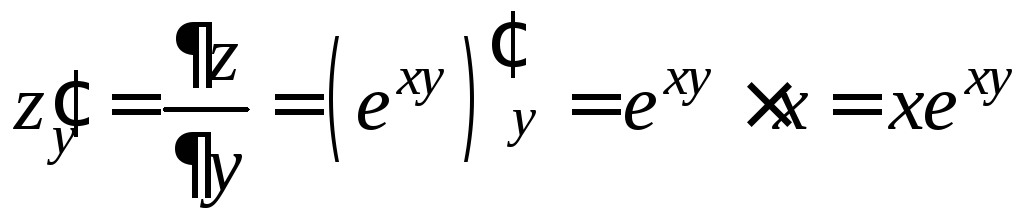Используя формулу (10.1), найдем дифференциал 1-го порядка:

.

Найдем частные производные 2-го порядка:

; ;

; .

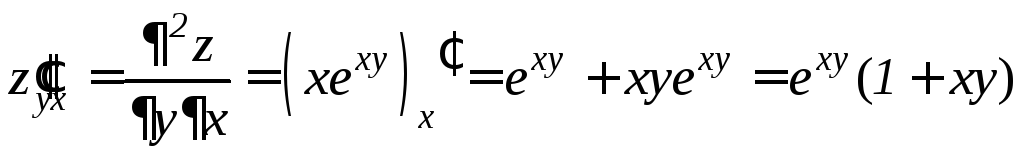Отметим, что справедливо равенство .

Используя формулу (10.3), найдем дифференциал 2-го порядка:

.

Пример 6. С помощью дифференциала вычислить приближенно , исходя из значения функциипри.

Решение. Вычислим значение функции при :

.

Вычислим приближенно приращении функции , заменяя его дифференциалом (формула 10.2), при:

.

Таким образом, используя формулу 10.2, получаем:

.

10.4. Экстремум функции нескольких переменных

Пусть функция u=f(M) определена в области D и точка M₀ является внутренней точкой этой области. Говорят, что функция f(M) имеет в точке M₀ экстремум (максимум или минимум), если существует такая окрестность точки M₀ , в которой для любой точки M из этой окрестности выполняется неравенство

.

Из определения экстремума следует, что если функция имеет экстремум в точке M₀ , то полное приращение этой функции в точкеM₀ удовлетворяет в некоторой окрестности точки M₀ одному из следующих условий:

И обратно, если в некоторой окрестности точки M₀ выполняется одно из этих неравенств, то функция f(M) имеет в точке M₀ экстремум.

Если в точке в точке M₀ функция f(M) имеет экстремум, то в этой точке ее частные производные либо равны нулю, либо не существуют

(10.4)

Точки, в которых выполняются условия (10.4), называются стационарными точками функции u=f(M). Точки, в которых частные производные равны нулю или не существуют, называются критическими.

Рассмотрим функцию двух переменных u=f(x,y) в окрестности стационарной точки M₀(x₀, y₀) . Обозначим

.

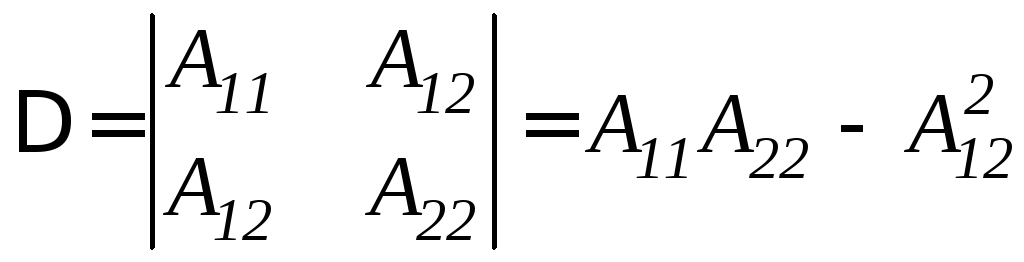Достаточные условия существования точек экстремума для функции двух переменных:

1) Если >0, то в точке M₀ экстремум, причем – максимум при A₁₁<0, минимум при A₁₁>0.

2) Если <0, то в точке M₀ экстремум отсутствует.

3) Если =0, то требуется дополнительное исследование на наличие экстремума данной функции в точке M₀.

Пример 7. Найти точки экстремума функции

.

Решение. Найдем стационарные точки данной функции, для этого вычислим частные производные функции и приравняем их нулю

Решая эту систему уравнений, находим, что существует четыре стационарных точки:

Теперь определим, есть ли в этих стационарных точках экстремумы. Для этого вычислим A₁₁, A₂₂, A₁₂ и . Поскольку

,

то для вычисления этих коэффициентов в найденных стационарных точках составим таблицу:

	M1	M2	M3	M4
A11	10>0	–10<0	–2	–2
A22	2	–4/3	0	0
A12	0	0	4	–4
	20>0	40/3>0	–16<0	–16<0
	min	max	экстремума нет	экстремума нет

Таким образом, в точке M₁(0; 0) функция имеет минимум, в точке M₂(–5/3; 0) – максимум, в точках M₃ и M₄ экстремума нет.