
- •Вопрос 1. Первообразная и ее общий вид
- •Вопрос 2. Свойства неопределенного интеграла
- •Вопрос 3. Интегрирование заменой переменной и подстановкой в неопределенном интеграле
- •Вопрос 4. Интегрирование по частям неопределенного интеграла
- •Вопрос 5. Необходимое условие интегрируемости функции.
- •Вопрос 6. Суммы Дарбу и их свойства.
- •Вопрос 7. Лемма Дарбу-Римана.
- •Вопрос 8. Критерий интегрируемости
- •Вопрос 9.Свойства интеграла Римана
- •Вопрос 10.Интегрируемость непрерывной функции
- •Вопрос 11. Интегрируемость ограниченной функции с конечным числом точек разрыва.
- •Вопрос 12. Интегрируемость функции, монотонной на отрезке.
- •Вопрос 13. Теоремы о среднем для интеграла.
- •Вопрос 14. Свойства интеграла с переменным верхним пределом интегрирования.
- •Вопрос 15. Формула Ньютона-Лейбница и её обобщение.
- •Вопрос 16. Интегрирование заменой переменной и по частям в определённом интеграле
- •Вопрос 17. Векторные пространство Rm, скалярные произведения, модуль, расстояние.
- •Вопрос 18. Критерии замкнутости в метрическом пространстве.
- •1 Критерий замкнутости
- •2 Критерий замкнутости
- •Вопрос 19. Свойство компактности в метрическом пространстве.
- •Вопрос 20. Компактность m-мерного отрезка.
- •Вопрос 21. Критерий компактности в Rm.
- •Вопрос 22. Критерий Коши и покоординатная сходимость.
- •Вопрос 23. Теорема Больцано-Вейерштрасса
- •Вопрос 24. Предел функции по направлению и предел по совокупности переменных.
- •Вопрос 25. Повторные и двойные пределы.
- •26. Непрерывность сложной функции многих переменных.
- •27. Теорема Коши о промежуточном значении функции.
- •28. Теоремы Вейерштрасса для функций многих переменных.
- •29. Дифференцируемость функции многих переменных, вид нелинейной части.
Вопрос 21. Критерий компактности в Rm.
Множество K в Rm – компактно <=> K – замкнуто и ограничено.
Доказательство.ПустьK– ограниченное замкнутое множество в Rm. Значит, имеется Br(x) включающийK. Брус П = произведения(k=1..n)[xk–r,xk+r] включающий Br(x) включающийK. Значит, F – замкнутое подмножество компакта. Значит, F – компакт.
Вопрос 22. Критерий Коши и покоординатная сходимость.
Xn=(x1(n),x2(n),…,xn(n))
Xn=(1/n, 1/n)->(0, 0)=0
X(n)-> X0, если для любой окрестностиX0существует номерN, такой что для всех номеровnбольших негоX(n) лежит в этой окрестности.
или
X(n)->
X0, если
для любого положительного эпсилон
существует номерN, такой
что для всех номеровnбольших него выполняется неравенство . Т.е.
. Т.е.
X(n)
ограничена,если
Замечание
X(n)ограничена – ограничена
– ограничена
Свойства
Предел единственный
Сходящаяся последовательность -> ограниченная последовательность
??
X(n)-> X0

Теорема Больцано-Вейерштрасса
Из любой ограниченной последовательности можно выделить сходящуюся подпоследовательность
Доказательство 4)
 рассмотрим
рассмотрим

Берём
 , тогда
, тогда
 , т.е.
, т.е.
Критерий Коши
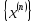 – фундаментальна, если
– фундаментальна, если

Теорема
 – сходящаяся вℝm
– сходящаяся вℝm фундаментальна вℝm
фундаментальна вℝm
Доказательство
Н=>метод
Д<=Пусть фундаментальна вℝm
фундаментальна вℝm
Возьмём
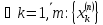 – она последовательность Коши
– она последовательность Коши
Берём


По критерию
Коши в ℝ=ℝ’ ,
т.е. X->X0, тогда
,
т.е. X->X0, тогда

Вопрос 23. Теорема Больцано-Вейерштрасса
Из любой ограниченной последовательности
 можно выделить сходящуюся
подпоследовательность.
можно выделить сходящуюся
подпоследовательность.
Доказательство
Пусть
 – ограничена
– ограничена
k=1, – тоже ограниченная последовательность
чисел, тогда (по т.Б-В)
– тоже ограниченная последовательность
чисел, тогда (по т.Б-В)

K=2,
рассмотрим – тоже ограниченная (подпоследовательность
оганиченной посл.), тогда (по т.Б-В)
– тоже ограниченная (подпоследовательность
оганиченной посл.), тогда (по т.Б-В)
 и т.д.
и т.д.
K=m,
рассмотрим – ограниченная, тогда (по т.Б-В)
– ограниченная, тогда (по т.Б-В)

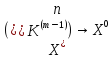 (покоординатно) => сходится вℝm
(покоординатно) => сходится вℝm
Вопрос 24. Предел функции по направлению и предел по совокупности переменных.
Функции многих переменных


Пример
 – параболоид вращения
– параболоид вращения
 – верхняя полусфера
– верхняя полусфера
Предел функции в точке
 , если определена в – открытом, кроме,
быть может, точки
, если определена в – открытом, кроме,
быть может, точки ,
,
По Коши

То же в окрестностях

По Гейне

Свойства
Коши Гейне
Предел единственный
Если
 то
то
Если
 , то
, то
 :
:
 =
= +
+
И другие арифметические свойства
Предел по совокупности переменных(илиm-кратный предел)
Расписываем определение по Коши подробнее


Предел в точке по направлению
 -вектор
-вектор
 =1
=1

 (t)=f(
(t)=f( )
)
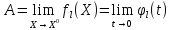
Замечание
Если пределы по каким-либо двум направлениям существуют и различны, то предела по их совокупности не существует.
Теорема
Если
 , то
, то
Доказательство
Берём
 Дано
Дано ,
,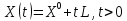

Берём
 и рассмотрим
и рассмотрим

Вопрос 25. Повторные и двойные пределы.
Пусть дано некоторое множество M в m-мерном пространстве, и точка Mo является его точкой сгущения. Тогда из M всегда можно извлечь такую последовательность отличных от Мо точек, которая сходилась бы к Мо как к предельной точке.
Кроме предела функции
 при одновременном стремлении всех
аргументов к их пределам, приходится
иметь дело и с пределами другого рода,
получаемыми в результате ряда
последовательных предельных переходов
по каждому аргументу в отдельности в
том или ином порядке. Первый предел
называетсяn-кратным(илидвойным,
тройными т. д. — при n = 1,2,3,...,n), а
последний —повторным.
при одновременном стремлении всех
аргументов к их пределам, приходится
иметь дело и с пределами другого рода,
получаемыми в результате ряда
последовательных предельных переходов
по каждому аргументу в отдельности в
том или ином порядке. Первый предел
называетсяn-кратным(илидвойным,
тройными т. д. — при n = 1,2,3,...,n), а
последний —повторным.
Ограничимся для простоты случаем функции двух переменных f(х,y). Допустим к тому же, что область изменения переменныхх,утакова, чтох(независимо от y) может принимать любое значение в некотором множестве для которогоаслужит точкой сгущения, но ему не принадлежит, и аналогичноу(независимо отх) изменяется в множествеYс точкой сгущенияb, не принадлежащей ему. Такую область можно было бы символически обозначить, как например, (а, а + Н;b,b+k) = (a, а + Н)x(b,b+k).
Если при любом фиксированном уизУсуществует для функцииf(x, у) (которая оказывается функцией лишь отx) предел прих->а, то этот предел, вообще говоря, будет зависеть от наперед фиксированного у:

Затем можно поставить вопрос о пределе функции F(у) при у->b:
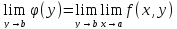
Это и будет один из двух повторных пределов. Другой получится, если предельные переходы произвести в обратном порядке:

Не следует думать, что повторные пределы эти необходимо равны. Может случиться также, что один из повторных пределов существует, а другой—нет.
Теорема.
Если 1)существует (конечный или нет) двойной предел

И 2)при любом у из У существует (конечный) простой предел по х

то существует повторный предел

равный двойному.
Докажем это для случая конечных А, а и Ь. Согласно определению предела функции, по заданному ε>0 найдется такое δ>0, что

лишь только
 (причем
х беретсяXиз а у из У).
Фиксируем теперь у так, чтобы выполнялось
неравенство ,
(причем
х беретсяXиз а у из У).
Фиксируем теперь у так, чтобы выполнялось
неравенство , и перейдем в (1) к пределу, устремив х к
а. Так как, ввиду 2),f(x,
у) при этом стремится к пределу ϕ (у), то
получим
и перейдем в (1) к пределу, устремив х к
а. Так как, ввиду 2),f(x,
у) при этом стремится к пределу ϕ (у), то
получим
Вспоминая, что у здесь есть любое число
из У, подчиненное лишь условию
 приходим к заключению, что
приходим к заключению, что

что и требовалось доказать.
