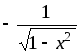- •Пример решения простейшего интеграла.
- •На будущее:
- •Наиболее популярные методы решения неопределённых интегралов
- •1. Замена переменной интегрирования.
- •2. Приведение к «табличному виду».
- •3. Замена функции.
- •4. Интегрирование «по частям»
- •Рациональные дроби
- •Метод «неопределённых коэффициентов»
- •6. Тригонометрические функции.
- •6.1. Интегралы типа ,.
- •6.2. Интегралы типа
- •6.3. Интегралы типа
- •6.4. Интегралы типа
- •6.5. Интегралы типа .
- •7. Тригонометрические подстановки
- •8. Интегралы с иррациональностью типа.
- •Приложение 2 Построение таблицы исходных данных и соответствующего ей совмещённого графика
- •Построение графика
- •Часть I. Неопределённый интеграл
УДК 517
Составители: В.Е.Кузема и др.
Научный редактор
Интегралы: Методические указания к РГР по курсу «Математика». Ч. 1. Неопределённый интеграл. / В.Е. Кузема и др.. Екатеринбург: УГТУ-УПИ, 2007. 64с.
Кратко излагаются основы интегрального исчисления, приводятся основные приёмы интегрирования, подкреплённые примерами с решениями, приводятся 25 вариантов заданий для этой части РГР и авторский образец выполнения и оформления такого задания.
Для более глубокого изучения материала, которому посвящена данная РГР, представлена достаточно обширная библиография.
Методические указания предназначены студентам и аспирантам всех специальностей и всех форм обучения, изучающим курс «Математика».
Библиогр.: 5 назв. Табл.7. Рис.3.Прил. 2.
Подготовлено кафедрой «Прикладная математика».
© «Уральский государственный технический университет – УПИ», 2007
Настоящие методические указания предназначены для успешного самостоятельного выполнения расчётно-графической работы (РГР) студентами любой специальности в рамках курса математики, читаемого в высшем техническом учебном заведении. Структурно данная РГР состоит из двух частей: «Неопределённые интегралы» и «Определённые интегралы». Успешное выполнение первой части предопределяет, по мнению авторов, столь же успешное выполнение и второй её части.
Для реализации поставленной задачи каждая часть предваряется краткой теоретической информацией с приведением указаний на литературные источники, в которых пользователи данных методических указаний могут более углублённо освоить как теоретические, так и практические положения соответствующих разделов математики, относящиеся к интегралам, и их практическому применению в инженерных расчётах.
Авторы также считают, эти методические указания могут быть полезны студентам старших курсов при подготовке курсовых и дипломных работ, а также аспирантам и соискателям, дабы освежить в памяти давно пройденное.
Обращение к исполнителям РГР.
Уважаемые студенты, не думайте, пожалуйста, что мы, авторы этих методических указаний задались садистской целью помучить Вас и сформировать у Вас чувство собственной умственной неполноценности. Наоборот, зная, что Вам придётся несколько позже осваивать такой очень важный и необходимый для любого знающего инженера раздел как «Дифференциальные уравнения», мы хотели, чтобы Вы так «набили руку» при решении вполне достаточного для данной цели числа неопределённых интегралов, чтобы при освоении указанного раздела Вы не особенно задумывались над технической стороной (взятия неопределённых интегралов) решения дифференциальных уравнений, а сосредоточились на сущности самих методов решения этих уравнений.
Ниже мы даём рекомендации, как выполнять РГР, но обязательным должно быть строгое следование представленным в соответствующих местах образцам.
При выполнении своего задания после копирования текста своего задания Вы можете использовать один из двух предлагаемых нами алгоритмов:
· используя соответствующую литературу[1-6], конспекты и справочники, не обращаясь к данным методическим указаниям самостоятельно взять Ваши интегралы (при условии изложения самопроверки). Это похвальный путь, ибо он свидетельствует о Вашей самодостаточности и не является, по нашему мнению, поводом со стороны преподавателя снижать Вам оценку. На наш взгляд для этого лучше всего подошли бы книги [2,3];
· кроме конспектов, литературы и справочников применить решение соответствующих аналогичных примеров данных методических указаний. Это тоже правильный поступок и не служит свидетельством Вашей слабости, а только показывает, что Вы мудры и следуете подсказкам своего «внутреннего голоса».
Желаем Вам упорства и получения глубокого внутреннего удовлетворения от проделанной работы!
Основные понятия
Неопределенный интеграл
В основе интегрального исчисления [1] лежит следующее положение:
если
на некотором интервале значений аргумента
![]() существует непрерывная функция
существует непрерывная функция![]() ,
то ей можно сопоставить другую также
непрерывную и, как минимум один раз
дифференцируемую, функцию
,
то ей можно сопоставить другую также
непрерывную и, как минимум один раз
дифференцируемую, функцию![]() ,
связанную с
,
связанную с![]() условием
условием![]() =
=![]() ,
т.е. функция
,
т.е. функция![]() равна
первой производной функции
равна
первой производной функции
 .
.
Отсюда
основной целью интегрального исчисления
является: по виду функции
![]() подобрать
каким-либо способом соответствующую
ей функцию
подобрать
каким-либо способом соответствующую
ей функцию![]() (именуемую в дальнейшемпервообразной).
Кратко это преобразование обозначается
(именуемую в дальнейшемпервообразной).
Кратко это преобразование обозначается

Появление
константы
![]() связано
с известным в дифференциальном исчислении
соотношением
связано
с известным в дифференциальном исчислении
соотношением![]() произвольная
функция
аргумента
произвольная
функция
аргумента
![]() Это соотношение отражает следующее
свойство: данной подынтегральной функции
Это соотношение отражает следующее
свойство: данной подынтегральной функции![]() можно сопоставитьбесконечное
множество
первообразных функций
можно сопоставитьбесконечное
множество
первообразных функций
![]() ,
отличающихся друг от друга на бесконечно
малое числовое значение.
,
отличающихся друг от друга на бесконечно
малое числовое значение.
Приведённая
выше фраза «подобрать каким-либо способом
соответствующую ей функцию
![]() »
означает следующее:
»
означает следующее:
если данной подынтегральной функции можно подобрать первообразную функцию в явном аналитическом виде, то неопределённый интеграл (1) называется «берущимся»;
в противном случае (а таких интегралов гораздо больше, чем берущихся) этот интеграл именуется «неберущимся». Этот факт становится важным при проведении инженерных и научных расчётов с использованием определённых интегралов. Во второй части указаний Вы познакомитесь с некоторыми популярными способами приближённого (численного) решения таких интегралов и сможете самостоятельно сопоставить эти способы (методы), чтобы в дальнейшем достаточно уверенно применять в конкретном случае тот или другой метод.
Основная трудность при взятии неопределённого интеграла состоит в том, что не существует единого «универсального» метода решения этой задачи. Есть интегралы, которые берутся только одним конкретным методом, в то время как остальные могут быть решены различными методами. В данном пособии приводится традиционная таблица неопределённых интегралов от простейших «элементарных» подынтегральных функций (табл.1).
При выполнении первой части данной РГР студентам придётся решить 14 неопределённых интегралов разного типа. К каждому из них необходимо применить какой-либо метод, приведённый в соответствующем разделе. В основе этих методов лежит «простая» идея: преобразовать подынтегральную функцию так, чтобы исходный интеграл либо прямо соответствовал «табличному», либо представлял собой алгебраическую сумму «табличных» интегралов.
Прежде чем переходить к ознакомлению с образцом выполненной РГР, неплохо было бы вспомнить отдельные свойства неопределённых интегралов.
Сначала
вспомним формулу дифференциала
функции
![]() :
:
![]() .
В сочетании с введённой выше связи
подынтегральной и первообразной
функциями
.
В сочетании с введённой выше связи
подынтегральной и первообразной
функциями
![]() и
и![]() ,
соответственно, эта формула позволяет
ввестидифференциал
первообразной функции:
,
соответственно, эта формула позволяет
ввестидифференциал
первообразной функции:
![]() =
=![]() .
.
Основные свойства неопределённых интегралов [1]
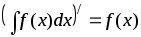 ─очень
полезное свойство, позволяющее
самостоятельно проверить правильность
взятия интеграла;
─очень
полезное свойство, позволяющее
самостоятельно проверить правильность
взятия интеграла;
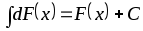 ─свойство-алгоритм
взятия интеграла;
─свойство-алгоритм
взятия интеграла;
 ;
;
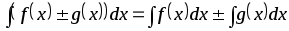 .
.
Основная
таблица неопределённых элементарных
интегралов
![]() [1].
[1].
|
№ п/п |
|
|
Примечания |
|
1 |
|
|
|
|
2 |
|
|
|
|
3 |
|
|
|
|
4 |
|
|
|
|
5 |
|
|
|
|
6 |
|
|
|
|
7 |
|
|
|
|
8 |
|
|
|
|
9 |
|
|
|
|
10 |
|
|
|
|
11 |
|
|
|
Табл.1. Основные (простейшие) интегралы
Пример решения простейшего интеграла.
Пример 0
![]()
 .
.
Рецепт.
Используя
свойство 4 (см. стр. 6), преобразуем
«интеграл от суммы функций» в «сумму
интегралов от функций»:
![]()
![]() +
+![]() +
+![]() +
+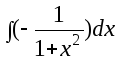 .
.
Нетрудно
заметить, что подынтегральная функция
первого интеграла
![]()
![]()
![]() .
Аналогичная картина и в остальных
интегралах:
.
Аналогичная картина и в остальных
интегралах:![]() =
=![]() ,
,![]() =
=![]() ,
,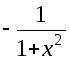 =
=![]() .
.
Если
вспомнить формулу дифференциала, то
получим
![]()
![]() +
+![]() +
+![]()
![]() ,
т.е. мы имеем дело с элементарными
«табличными» интегралами.
,
т.е. мы имеем дело с элементарными
«табличными» интегралами.
Тогда
конечный итог:
![]()
![]() .
.
На будущее:
тактика вычисления любых неопределённых интегралов должна сводиться к такому преобразованию подынтегральной функции, чтобы её структура была похожа на структуру только что приведённого примера.
Поскольку многообразие подынтегральных функций практически неограниченно, то ниже предлагаются несколько «стандартных» приёмов преобразования подынтегральных функций, чтобы Вам не приходилось заново «изобретать велосипед».
Наиболее популярные методы решения неопределённых интегралов
1. Замена переменной интегрирования.
Пример
1.
![]()
![]()
Рецепт.
Вводим замену
![]() .
Отсюда:
.
Отсюда:![]() (вспомним
формулу дифференциала)
(вспомним
формулу дифференциала)![]()
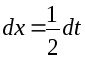 .
Тогда
.
Тогда![]() (обратная
подстановка)
(обратная
подстановка)![]() .
.
Пример
2.
![]()
![]()
В таблице элементарных интегралов имеется формула аналогичного интеграла:
![]() Однако
чаще же всего встречается более общий
вариант этого интеграла:
Однако
чаще же всего встречается более общий
вариант этого интеграла:![]() ,
где
,
где![]() ─ некая числовая константа.
─ некая числовая константа.
Рецепт.
Выносим
![]() из знаменателя (а, значит, и из-под знака
интеграла):
из знаменателя (а, значит, и из-под знака
интеграла):
 и
делаем замену:
и
делаем замену:
 .
Тогда
.
Тогда![]() .
А это уже знакомый табличный интеграл.
Отсюда
.
А это уже знакомый табличный интеграл.
Отсюда![]() .
Проводим обратную подстановку
.
Проводим обратную подстановку![]() и получаем в результате
и получаем в результате![]()
![]()
Полученным интегралом рекомендуем пополнить уже имеющуюся таблицу.
2. Приведение к «табличному виду».
Пример
3.
![]()
![]() Здесь рассматривается вариант, при
котором дискриминант знаменателя
существенно отрицательный (остальные
варианты исследуются ниже).
Здесь рассматривается вариант, при
котором дискриминант знаменателя
существенно отрицательный (остальные
варианты исследуются ниже).
Рецепт. Преобразуем трёхчлен знаменателя к виду, похожему на квадратный двучлен табличного интеграла, рассмотренного в Примере 2. Последовательность действий должна быть следующей:
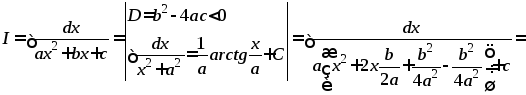

Очевидно,
что этот интеграл по своей структуре
полностью соответствует интегралу
Примера
2: переменной
![]() этого интеграла соответствует переменная
этого интеграла соответствует переменная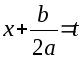 ,
а множителю
,
а множителю![]() соответствует радикал:
соответствует радикал: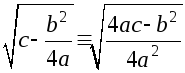
 .
Далее
.
Далее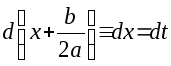 .
Отсюда решение интеграла:
.
Отсюда решение интеграла:![]()
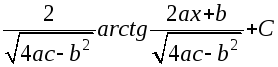
N.B.! Помните, что нельзя полностью доверять авторам любого учебного пособия (кто из нас не без греха?), в том числе и авторам данного пособия. Поэтому убедительная просьба: для проверки правильности взятия интеграла старайтесь почаще применять первое свойство интегралов!
3. Замена функции.
Для этого приёма характерно многообразие вариантов замены какой-либо функции, входящей в подынтегральную функцию. Удача чаще всего приходит только в случае перебора нескольких вариантов.
Пример
4.
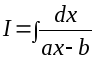 .
.
Рецепт.
Здесь безальтернативный вариант замены:
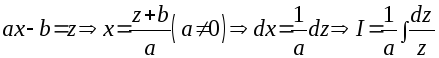 .
Это – табличный интеграл:
.
Это – табличный интеграл: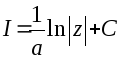 .
Обратная подстановка
.
Обратная подстановка![]() приводит к конечному результату:
приводит к конечному результату: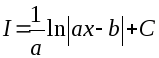 .
.
Пример
5.

Рецепт.
Опытный взгляд обнаружит интересную
дробь
![]() ─ дифференциал функции
─ дифференциал функции![]() ,
а в числителе дроби встречается именно
такая функция. Отсюда должна появиться
естественная мысль сделать замену:
,
а в числителе дроби встречается именно
такая функция. Отсюда должна появиться
естественная мысль сделать замену:![]() .
Тогда
.
Тогда![]()
![]()
![]()
![]()
![]() .
В результате этой подстановки имеем
табличный интеграл:
.
В результате этой подстановки имеем
табличный интеграл: .
Обратная подстановка приводит к конечному
результату
.
Обратная подстановка приводит к конечному
результату![]()
 .
.
К
этой же группе интегралов, требующих
замены функции, относятся такие, в
составе которых имеются радикалы
![]() ой
степени
ой
степени
![]() ,
т.е. компоненты типа
,
т.е. компоненты типа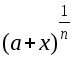 .
Очевидно, такой радикал надо заменить
какой-либо переменной того же типа.
.
Очевидно, такой радикал надо заменить
какой-либо переменной того же типа.
Пример
6.
![]()
![]() .
.
Рецепт.
Здесь
![]() .
Очевидна замена
.
Очевидна замена![]() =
=![]() тогда
тогда![]() =
=![]()
![]()
![]()
![]()
![]()
![]() .
Тогда интеграл легко приводится к
.
Тогда интеграл легко приводится к![]()
![]() =
=
=
=![]()
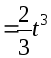 +С.
+С.
Обратная
подстановка даёт конечный результат:
![]()
 =
= +С.
+С.