matrix

1. МАТРИЦЫ И ОПРЕДЕЛИТЕЛИ

1.1.Матрицы

1.1.1.Определение матрицы. Виды матриц

ОПРЕДЕЛЕНИЕ. Матрицей размера m n называется прямоугольная таблица чисел aij , i 1,2,..., m ; j 1,2,...,n , расположенных в m строках и n столбцах:

a11

A a21

am1

a12 a1n a22 a2n

.

am2 amn

Числа aij называются элементами матрицы.

Матрица размера 1 n называется матрицей-строкой и имеет вид:

А a1 a2 a3 ...an . Матрица размера m 1 называется матрицей-столбцом и имеет вид:

	a1
	a
В	2	.

...

am

ОПРЕДЕЛЕНИЕ. Матрица называется квадратной, если число строк равно числу столбцов ( m n ), при этом число n называется порядком матрицы.

Пример квадратной матрицы 3-го порядка:

			a 1 1	a 1 2	a 1 3
A			a 2 1	a 2 2	a 2 3
						.
			a 3 1	a 3 2
					a 3 3

ОПРЕДЕЛЕНИЕ. Ряд элементов квадратной матрицы, лежащих на отрезке, соединяющем левый верхний угол с правым нижним, называется главной диагональю, а на отрезке, соединяющем правый верхний угол с левым нижним, – побочной диагональю матрицы. Элементы, стоящие на главной диагонали,

имеют вид aii , i 1,2,...,n .

ОПРЕДЕЛЕНИЕ. Квадратная матрица, у которой все элементы, стоящие ниже (или выше) главной диагонали, равны нулю, называется верхней (нижней)

треугольной.

Пример верхней треугольной матрицы третьего порядка:

4

a11		a12
	0	a22
	0	0

a13

a23 . a33

ОПРЕДЕЛЕНИЕ. Квадратная матрица, у которой все элементы, стоящие

выше и ниже главной диагонали, равны нулю ( aij 0						при i j ), называется
диагональной:
a11		0	...	0
	0	a22	...	0
...		...	...	...	.
	0	0	...
				ann

Очевидно, что диагональная матрица является одновременно и верхней треугольной, и нижней треугольной.

ОПРЕДЕЛЕНИЕ. Квадратная диагональная матрица с единичными элементами на главной диагонали называется единичной и обозначается буквой Е. Например, единичная матрица 3-го порядка имеет вид:

	1		0	0
E		0	1	0
					.
		0	0	1

ОПРЕДЕЛЕНИЕ. Если все элементы матрицы равны нулю, то матрица называется нулевой и обозначается O .

ОПРЕДЕЛЕНИЕ. Матрицы A и B называются равными, если они имеют одинаковые размеры и все их соответствующие элементы совпадают.

1.1.2.Операции над матрицами и их свойства

1.Сложение матриц

ОПРЕДЕЛЕНИЕ. Суммой матриц A aij и	B bij	одинаковой раз-
мерности m n называется матрица C A B ,	элементы	которой равны
cij = aij +bij , где i 1,2,..., m ; j 1,2,...,n .
Свойства операции сложения:
С в о й с т в о 1 . A B B A.

С в о й с т в о 2 .	A B C A B C .
С в о й с т в о 3 .	A O A.

З а м е ч а н и е . О п е р а ц и ю в ы ч и та н и я м а тр и ц о п р е д е л я е м к а к о б р а тн у ю д л я о п е р а ц и и с л о ж е н и я т . е . A B C , п р и - ч ё м C B A . Та к и м о б р а з о м cij = aij -bij , i 1,2,..., m ; j 1,2,...,n .

5

2. Умножение матрицы на число

ОПРЕДЕЛЕНИЕ. Произведением матрицы A на число называется мат-

рица C A,	элементы которой удовлетворяют равенству: cij aij , где
i 1,2,..., m ; j	1,2,...,n .

Свойства операции умножения на число:

Св о й с т в о 4. A 1 A O .

Св о й с т в о 5. A A .

Св о й с т в о 6. A B A B .

Св о й с т в о 7. A A A .

Св о й с т в о 8. 0 A O ; 1 A A .

За м е ч а н и е. Используя операцию умножения на число, операция вычитания матриц определяется следующим образом A B A 1 B .

ПРИМЕР: Найдите 3А+2В, если

2 1			1	,		2	1		0
A	0 1				B		2		2		.
			4			3
6		3	3		4		2	0			2		5	3
Решение: 3A 2B	0	3	12			6	4	4				6	7	8	.

3. Умножение матриц

ОПРЕДЕЛЕНИЕ. Произведением матрицы A размерности (m n) на мат-

рицу B размерности (n k) называется матрица C=AB размерности (m k), элементы которой находятся по формуле:

n
cij aiqbqj ai1b1 j ai2b2 j ainbnj , где i 1,2,..., m ;	j 1,2,...,k ,
q 1

т.е. cij равен сумме произведений элементов i-й строки матрицы A на элементы

j–го столбца матрицы B. Число столбцов первой матрицы должно равняться числу строк второй матрицы.

			4		1
ПРИМЕР: Найдите АВ, если A 1 2	3 ,	B		5	2
						.
				6	3

Решение: C AB 1 4 2 5 3 6 1 1 2 2 3 3 32 14 ,

размерность матрицы C 1 2 .

Свойства операции умножения:

С в о й с т в о 9. AB C A BC .

6

Св о й с т в о 10. A B C AC BC .

Св о й с т в о 11. A B C AB AC .

ОПРЕДЕЛЕНИЕ. Матрицы A и B называются перестановочными (ком-

мутирующими), если AB BA.
В общем случае произведение матриц не коммутативно: AB BA.
				1		2	1	2
ПРИМЕР: Найдите AB и BA, если A					3		, B	2	.
						4	1
1	2 1	2	3	6			1	2 1			2	7		10
Решение: AB				14	, B A					3			7	10	.
3	4 1	2	7				1	2			4

Св о й с т в о 12. AE EA A.

Св о й с т в о 13. AO OA O .

4. Транспонирование матрицы

ОПРЕДЕЛЕНИЕ. Если матрица А имеет размерность m n , то транспо-

нированная матрица AT имеет размерность n m , а её элементы определя-

ются равенством aTji aij .

Иными словами, строки матрицы становятся столбцами с теми же номерами, а столбцы – строками:

	a		a	a					a11			a21 am1
	11		12		1n				a12			a22 am2
	a	21	a	a			T
A			22		2n		A
									.
			am2									a2n
	am1			amn					a1n					amn
Например, для										1		4
				1		2	3
									T		2	5
				A		5	6		, A				.
				4							3	6

ОПРЕДЕЛЕНИЕ. Если квадратная матрица A совпадает со своей транспонированной, т.е. AT A , то такая матрица называется симметрической.

ОПРЕДЕЛЕНИЕ. Если квадратная матрица A отличается множителем 1 от своей транспонированной, т.е. AT A , то такая матрица называется кососим-

метрической.

Операция транспонирования имеет следующие свойства:

Свойство 14. AT T A. Свойство 15. A B T AT BT .

7

Свойство 16. AB T BT AT .

1.2.Определители второго, третьего и n-го порядков

1.2.1. Определение определителя 2-го 3-го и n- го порядков

ОПРЕДЕЛЕНИЕ. Определителем второго порядка квадратной матрицы

a

a

a12a21 и обозначаемое

11

12

называется число, равное a11a22

a21

a22

A

d e t

a

1 1

a1 2

a1 1 a 2 2 a1 2 a 2 1 .

a 2 1

a 2 2

1

2

ПРИМЕР:

1 4 3 2 2 .

3

4

ОПРЕДЕЛЕНИЕ. Определителем третьего порядка квадратной матрицы

	a11	a12	a13
A		a22	a23
	a21			называется число, равное
		a32	a33
	a31
							a11	a12	a13
						det	a21	a22	a23
							a31	a32	a33

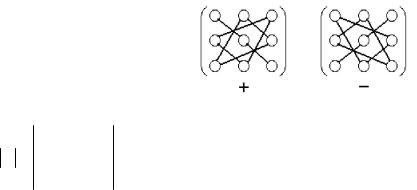
a11a22 a33 a12 a23a31 a13a21a32 a13a22 a31 a12 a21a33 a11a23a32 .

Это выражение получается по правилу треугольников (правилу Саррюса), его можно пояснить следующими схемами, на которых элементы, входящие в одно произведение с указанным знаком, соединены отрезками.

ПРИМЕР:

1 4 2

0 3 1

2 1 5

1 3 5 4 1 2 2 0 1 2 3 2 1 1 1 4 0 5 20 .

Чтобы дать определение определителя n-го порядка нужно ввести некоторые новые понятия.

8

ОПРЕДЕЛЕНИЕ. Перестановкой из n чисел 1,2,…, n называется всякое расположение этих чисел в определённом порядке. Число перестановок из n чисел равно n!.

ОПРЕДЕЛЕНИЕ. Числа i, j составляют инверсионную пару в перестановке, если i>j, но i встречается в перестановке раньше, чем j.

ОПРЕДЕЛЕНИЕ. Перестановка называется чётной, если число инверсионных пар чётно, и нечётной, если - нечётно.

ОПРЕДЕЛЕНИЕ. Преобразование перестановки, при котором меняются местами два символа, называется транспозицией.

Теорема. Всякая транспозиция меняет чётность перестановки.

Две перестановки, записанные другом под другом, образуют подстановку. Канонической подстановкой называется подстановка вида

1	2		3 n
	2			.
1			3 n

Число инверсионных пар в обеих перестановках, образующих подстановку, определяет чётность подстановки. Справедливо утверждение: транспозиция не изменяет четности подстановки.

Введённые выше понятия позволяют дать определение определителя любого порядка в общем виде:

ОПРЕДЕЛЕНИЕ. Определителем квадратной матрицы n-го порядка называется алгебраическая сумма n! слагаемых, каждое из которых есть произведение элементов матрицы, взятых по одному из каждой строки и каждого столбца, причём слагаемое входит со знаком плюс, если подстановка, образованная индексами элементов матрицы чётная и со знаком минус – если нечётная. Согласно этому определению определитель n-го порядка записывается в виде

	a11	a12	a1n
	a21	a22	a2n	1 s a1 1a2 2 an n ,
	an1	an2	ann
где s - чётность подстановки				1	2		3 n
					2		.
				1			3 n

1.2.2 Свойства определителей

Перечислим свойства определителей для определителей n -го порядка.

Для наглядности эти свойства проиллюстрированы на примерах определителей третьего порядка.

9

Св о й с т в о 1 . Определитель матрицы А не меняется при ее транспонировании: AT A .

Св о й с т в о 2 . При перестановке местами двух строк (столбцов) определитель меняет знак на противоположный. Например,

a11	a12	a13		a21	a22	a23
a21	a22	a23		a11	a12	a13	.
a31	a32	a33		a31	a32	a33

Св о й с т в о 3 . Определитель, содержащий две одинаковые строки (два одинаковых столбца), равен нулю.

Св о й с т в о 4. Общий множитель для элементов некоторой строки (столбца) определителя можно вынести за знак определителя:

k a11	a12	a1 3		a11	a12	a13
k a 2 1	a 22	a 23	k	a 21	a 22	a2 3	, k co n st .
k a3 1	a3 2	a33		a31	a32	a3 3

Это свойство можно сформулировать иначе: умножение всех элементов некоторой строки (столбца) определителя на число k равносильно умножению определителя на это число.

С в о й с т в о 5. Если все элементы некоторой строки (столбца) определителя равны нулю, то и определитель равен нулю. Например

a11	a12	a13
0	0	0 0

.

a31 a32 a33

Св о й с т в о 6. Если элементы двух строк (столбцов) определителя пропорциональны, то определитель равен нулю.

Св о й с т в о 7. Если каждый элемент некоторой строки (столбца) определителя представляет собой сумму двух слагаемых, то такой определитель можно представить в виде суммы двух определителей. Например

			a/	a//	a	a		a/	a	a		a//	a	a
			11	11	12	13		11	12	13		11	12	13
			a/	a//	a	a		a/	a	a		a//	a	a
			21	21	22	23		21	22	23		21	22	23	.
			a/	a//	a	a		a/	a	a		a//	a	a
			31	31	32	33		31	32	33		31	32	33

С в о й с т в о 8 . Если к элементам какой-нибудь строки (столбца) определителя прибавить соответствующие элементы другой строки (столбца), умноженные на произвольный множитель k, то величина определителя не изменится.

Например

10

aij :

a11	k a12	a12	a13		a11	a12	a13
a21	k a22	a22	a23		a21	a22	a23	.
a31	k a32	a32	a33		a31	a32	a33

З а м е ч а н и е : п ользуясь свойством 8, можно, не меняя величину определителя, все элементы некоторой строки (столбца) определителя, кроме одного, сделать равными нулю.

С в о й с т в о 9 . Определитель произведения квадратных матриц равен произведению их определителей.

ОПРЕДЕЛЕНИЕ. Минором Mij элемента aij квадратной матрицы А называ-

ется определитель матрицы, полученной из матрицы А вычеркиванием i-й строки и j-го столбца, на пересечении которых стоит элемент aij.

ПРИМЕР: Найдите минор M22 элемента a22 матрицы 3-го порядка

							a11		a12	a13
					A		a		a	a
								21	22	23	.
							a		a	a
								31	32	33
Решение: M 22			a11	a13		.
			a31	a33

ОПРЕДЕЛЕНИЕ. Алгебраическим дополнением Aij элемента aij квадрат-

ной матрицы А называется минор Mij этого элемента со знаком (–1)i+j, где i – номер строки, а j – номер столбца, на пересечении которых стоит элемент

					Aij 1 i j Mij .
ПРИМЕР:
1		2	3				1	3		12, A22 1	4
	4	5	6		: M22							M22	12 .
Для матрицы							7	9
	7	8	9

Те орема . Определитель численно равен сумме произведений элементов любой его строки (столбца) на соответствующие им алгебраические дополнения

n

det A A aik Aik ai1Ai1 ai2 Ai2 ...ain Ain ,i 1,2,...,n .

k 1

Для определителя 3-го порядка это разложение имеет вид

		a11	a12	a13
A		a21	a22	a23	ai1 Ai1 ai2Ai2 ai3Ai3, i 1, 2, 3.
		a31	a32	a33

11

При разложении по элементам первой строки для определителя 3 –го порядка имеем,

a11

a12

a13

a22

a23

a21

a23

a21

a22

A

a

a

a

a

a

a

21

22

23

11

a

a

12

a

a

13

a

a

a31

a32

a33

32

33

31

33

31

32

ПРИМЕР:

Вычислим определитель 3-го порядка разложением по элементам первой строки:

	2	0	5		3	16		1	16		1	3		30 16 5 1 92 5 87.
	1	3	16	2			0			5			2
					1	10		0	10		0	1
	0	1	10

В к а ч е с тв е с л е д с т в и я и з п р и ве д ё н н о й вы ш е те о р е м ы п о л у ч а - е м с л е д у ю щ е е с в о й с т в о :

С в о й с т в о 10. Сумма произведений элементов любой строки (столбца) определителя на алгебраическое дополнение соответствующих элементов другой строки (столбца) равна нулю.

1.2.3 Методы вычисления определителей произвольного порядка

Методы вычисления определителей n-го порядка основаны на рассмотренных выше свойствах определителей, справедливых для определителей любого порядка: определитель n-го порядка равен сумме произведений элементов любой его строки (столбца) на соответствующие им алгебраические дополнения.

Тем самым определитель n-го порядка мы выражаем через определители (n-1)- го порядка, те – через определители (n-2)-го порядка, и т.д., пока не дойдем до определителей 3-го или 2-го порядка, правила вычисления для которых заданы.

1. Метод разложения по строке или столбцу (метод понижения порядка):

n

det A A aik Aik ai1 Ai1 ai2 Ai2 ...ain Ain .

k 1

ПРИМЕР. Вычислим определитель 4-го порядка

2 1 0 1

0 1 1 2

A

3 1 3 2

3 1 1 6

методом понижения порядка.

12

Решение:
						2	1			0						1												1								1							2
						0	1 1									2					2 1 1 1
		A																										1						3 2
						3	1			3						2												1						1									6
						3	1			1						6
1 1 1 2														0 1 2												0 1 1 3														0 1					2		1 1 1 4												0 1 1
													3						3 2																					3			1		2														3			1	3
													3			1								6																3			1		6														3			1	1
							1 1								3	2												1 2								1							2					1 3						1 3
2 1							1								1	6								1 1												1							6	2 1										1			1
									3						2																	3				2													3			3
0 1 1 1																	1 1 1 2																									2 1 1 3
									1		6																					3		6															3			1
							1 1			1						3										1 2				3				3									1				1 3				3					1
0 1											1					1							1 1							3				1											1						3	1

2 16 8 8 12 12 6 6 0.

Вычисления можно упростить, преобразовав определитель так, чтобы в строке или столбце было как можно больше нулевых элементов. Приведем определитель к виду, в котором a11 1 , а остальные элементы первого столбца равны нулю. Для этого переставим первый и четвертый столбцы, при этом определитель изменит знак. Обозначим строки определителя через 1, 2 , 3 , 4 и обратим в нули элементы первого столбца во второй, третьей и четвертой строках

с помощью							следующих				преобразований					строк: 2 2 1,					3 2 1 ,
4 6 1.
						2	1	0	1				1	1	0	2			3	1	4
						0	1	1	2				0	3	1	4
		A																	1 3		1	.
						3	1	3	2				0	1	3	1
																			7	1	9
						3	1	1	6				0	7	1	9

В полученном определителе третьего порядка переставим первую и вторую строки (определитель сменит знак) и вычтем из новых второй и третьей строки

первую, умноженную, соответственно, на 3 и 7:

13