М.В.Москалец

МЕТОД МАТРИЦЫ РАССЕЯНИЯ

В ТЕОРИИ КВАНТОВОГО ТРАНСПОРТА

Учебное пособие

Представлен подход к описанию транспортных явлений в мезоскопических структурах,основанный на том,что процесс протекан ия тока рассматривается как процесс рассеяния свободных носителей тока на потенциале,соответствующем таким структурам.Описан как стаци онарный,так и нестационарный режимы квантового транспорта . В частности рассмотрен эффект генерирования постоянного тока образцом,параметы которого периодически изменяются со временем.

Предназначено для научных работников,преподавателей и ст удентов старших курсов,специализирующихся в области физики конде нсированного состояния,микроэлектроники и нанофизики.Необходимо з нание основ квантовой механики и статистической физики.

Содержание

Предисловие		9
1.Формализм Ландауэра-Бьюттикера		11
1.1.Матрица рассеяния. . . . . . . . . . . . . . . . . . . . . . .		11
1.1.1.Свойства матрицы рассеяния. . . . . . . . . . . . .		14
1.1.1.1.Свойство унитарности. . . . . . . . . . . .		14
1.1.1.2.Свойства,вытекающие из микрообратимо-
сти движения. . . . . . . . . . . . . . . . .		17
1.2.Оператор тока. . . . . . . . . . . . . . . . . . . . . . . . . .		21
1.3.Постоянный ток и функция распределения. . . . . . . . . .		27
1.3.1.Сохранение постоянного тока. . . . . . . . . . . . .		30
1.3.2.Разность потенциалов. . . . . . . . . . . . . . . . . .		32
1.3.3.Разность температур. . . . . . . . . . . . . . . . . .		35
1.4.Примеры. . . . . . . . . . . . . . . . . . . . . . . . . . . . .		36
1.4.1.Матрица рассеяния с размерностью	1 × 1 . . . . . .	36
1.4.2.Матрица рассеяния с размерностью	2 × 2 . . . . . .	37
1.4.3.Матрица рассеяния с размерностью	3 × 3 . . . . . .	39
1.4.4.Образец с двумя квази-одномерными проводниками		41
1.4.5.Ток,при наличии потенциального контакта. . . . . .		44
1.4.6.Кольцо с рассеивателем. . . . . . . . . . . . . . . .		46
1.4.6.1.Спектр. . . . . . . . . . . . . . . . . . . . .		48
1.4.6.2.Циркулирующий в кольце ток. . . . . . . .		49
2.Флуктуации тока		52
2.1.Качественное рассмотрение. . . . . . . . . . . . . . . . . . .		54
2.1.1.Тепловой шум. . . . . . . . . . . . . . . . . . . . . .		54
2.1.2.Дробовой шум. . . . . . . . . . . . . . . . . . . . . .		57
2.1.3.Смешанный шум. . . . . . . . . . . . . . . . . . . . .		58
2.2.Флуктуации тока в образце с непрерывным спектром. . . .		66
2.2.1.Коррелятор токов. . . . . . . . . . . . . . . . . . . .		66
2.2.2.Коррелятор токов в частотном представлении. . . .		69

3

Содержание

2.2.2.1.Коррелятор входящих токов. . . . . . . . .	70
2.2.2.2.Коррелятор токов входящих и рассеянных
электронов. . . . . . . . . . . . . . . . . .	71
2.2.2.3.Коррелятор токов рассеянных электронов.	74
2.2.3.Спектральная плотность шума в случае не зависящей
от энергии матрицы рассеяния. . . . . . . . . . . . .	75
2.2.4.Спектральная плотность шума на нулевой частоте. .	78
2.2.4.1.Закон сохранения для шума на нулевой ча-
стоте. . . . . . . . . . . . . . . . . . . . . .	80
2.2.4.2.Правило знаков для корреляторов токов. .	81
2.2.4.3.Образец с двумя контактами. . . . . . . .	83
2.2.5.Фактор Фано. . . . . . . . . . . . . . . . . . . . . . .	85
3.Нестационарная теория рассеяния	87
3.1.Уравнение Шредингера с периодическим возмущением. . .	87
3.1.1.Теория возмущения. . . . . . . . . . . . . . . . . . .	88
3.1.2.Метод функций Флоке. . . . . . . . . . . . . . . . .	92
3.1.3.Однородный осциллирующий потенциал. . . . . . .	96
3.2.Матрица рассеяния Флоке. . . . . . . . . . . . . . . . . . .	97
3.2.1.Свойства матрицы рассеяния Флоке. . . . . . . . .	98
3.2.1.1.Свойство унитарности. . . . . . . . . . . .	98
3.2.1.2.Свойства,вытекающие из микрообратимо-
сти движения. . . . . . . . . . . . . . . . .	99
3.3.Оператор тока. . . . . . . . . . . . . . . . . . . . . . . . . .	100
3.3.1.Переменный ток. . . . . . . . . . . . . . . . . . . . .	102
3.3.2.Постоянный ток. . . . . . . . . . . . . . . . . . . . .	103
3.4.Адиабатическое приближение для матрицы рассеяния Фло ке	105
3.4.1.Квазистационарная матрица рассеяния. . . . . . . .	106
3.4.2.Нулевое приближение. . . . . . . . . . . . . . . . .	107
3.4.3.Приближение первого порядка. . . . . . . . . . . . .	108
3.5.Выход за рамки адиабатического приближения. . . . . . . .	113
3.5.1.Матрица рассеяния в смешанном представлении. . .	113
3.5.2.Точечный рассеивающий потенциал. . . . . . . . . .	116
3.5.3.Двух-барьерный потенциал. . . . . . . . . . . . . .	124
3.5.3.1.Адиабатическое приближение. . . . . . . .	135

4

Содержание

3.5.4.Условие унитарности для матрицы рассеяния,пред-
ставленной в виде сумы по траекториям. . . . . . . .	137
3.5.5.Выражение для тока в случае,если матрица рассея-
ния представлена в виде суммы по траекториям. . .	139
4.Генерирование постоянного тока	146
4.1.Стационарный поток частиц. . . . . . . . . . . . . . . . . .	146
4.1.1.Функция распределения. . . . . . . . . . . . . . . .	146
4.1.2.Адиабатический режим:Линейный по частоте ток. .	149
4.1.3.Квадратичный по частоте ток. . . . . . . . . . . . . .	157
4.2.Квантовый эффект насоса. . . . . . . . . . . . . . . . . . .	159
4.2.1.Квазичастичная картина динамического генерирова-
ния постоянного тока. . . . . . . . . . . . . . . . . .	159
4.2.2.Интерференционный механизм генерирования по-
стоянного тока. . . . . . . . . . . . . . . . . . . . . .	160
4.3.Одно-параметрическое адиабатическое генерирование тока	164
5.Генерирование переменного тока	167
5.1.Адиабатический переменный ток. . . . . . . . . . . . . . . .	167
5.2.Ток при наличии внешнего переменного напряжения. . . . .	172
5.2.1.Операторы вторичного квантования для первичных и
рассеяных электронов. . . . . . . . . . . . . . . . . .	175
5.2.2.Переменный ток. . . . . . . . . . . . . . . . . . . . .	180
5.2.3.Постоянный ток. . . . . . . . . . . . . . . . . . . . .	181
5.2.4.Постоянный ток в адиабатическом приближении. . .	182
6.Шум динамического рассеивателя	188
6.1.Спектральная плотность шума. . . . . . . . . . . . . . . . .	188
6.2.Спектральная плотность шума на нулевой частоте. . . . . .	196
6.3.Шум в адиабатическом режиме. . . . . . . . . . . . . . . . .	200
6.3.1.Тепловой шум. . . . . . . . . . . . . . . . . . . . . .	200
6.3.2.Низкотемпературный дробовой шум. . . . . . . . . .	202
6.3.3.Высокотемпературный дробовой шум. . . . . . . . .	204
6.3.4.Дробовой шум в широком интервале температур. . .	205

5

Содержание

6.3.5.Зависимость шума от частоты Ω0 возмущения рассе-
ивателя. . . . . . . . . . . . . . . . . . . . . . . . . .	207
7.Теплоперенос через динамический образец	209
7.1.Постоянный поток тепла. . . . . . . . . . . . . . . . . . . .	209
7.1.1.Генерирование тепла динамическим рассеивателем.	213
7.1.2.Перенос тепла между резервуарами. . . . . . . . . .	213
7.2.Потоки тепла в адиабатическом режиме. . . . . . . . . . . .	216
7.2.1.Конечные температуры. . . . . . . . . . . . . . . . .	217
7.2.2.Низкие температуры. . . . . . . . . . . . . . . . . .	219
8.Динамический мезоскопический конденсатор	221
8.1.Общая теория для одноканального рассеивателя. . . . . . .	222
8.1.1.Амплитуды рассеяния. . . . . . . . . . . . . . . . . .	222
8.1.2.Условия унитарности. . . . . . . . . . . . . . . . . .	223
8.1.3.Зависящий от времени ток. . . . . . . . . . . . . . .	224
8.1.4.Поток тепла. . . . . . . . . . . . . . . . . . . . . . .	226
8.1.5.Тепловой поток и квадрат тока. . . . . . . . . . . . .	227
8.2.Емкость кирального одномерного кольца. . . . . . . . . . .	229
8.2.1.Модель и амплитуда рассеяния. . . . . . . . . . . .	230
8.2.2.Унитарность. . . . . . . . . . . . . . . . . . . . . . .	234
8.2.3.Калибровочная инвариантность модели. . . . . . . .	236
8.2.4.Зависящий от времени ток. . . . . . . . . . . . . . .	240
8.2.5.Высокотемпературный ток. . . . . . . . . . . . . . .	243
8.2.6.Линейный отклик. . . . . . . . . . . . . . . . . . . .	245
8.2.6.1.Проводимость при нулевой температуре. .	245
8.2.6.2.Проводимость в пределе низких частот. . .	247
8.2.7.Нелинейный низкочастотный режим. . . . . . . . . .	249
8.2.8.Релаксационный ток,вызванный скачком потенциала	253
8.2.8.1.Высокотемпературный ток. . . . . . . . . .	254
8.2.8.2.Низкотемпературный ток. . . . . . . . . .	255
8.2.8.3.Эмитированный заряд. . . . . . . . . . . .	258
9.Квантовые электронные цепи с регулируемым источником ча	-
стиц	262

6

Содержание

9.1.Режим квантованной эмиссии. . . . . . . . . . . . . . . . .	262
9.1.1.Модельная волновая функция. . . . . . . . . . . . .	267
9.2.Квантование дробового шума. . . . . . . . . . . . . . . . . .	268
9.2.1.Вероятностная интерпретация дробового шума. . .	272
9.3.Двухчастичный источник. . . . . . . . . . . . . . . . . . . .	274
9.3.1.Амплитуда рассеяния. . . . . . . . . . . . . . . . . .	274
9.3.2.Адиабатическое приближение. . . . . . . . . . . . .	275
9.3.2.1.Зависящий от времени ток. . . . . . . . . .	276
9.3.3.Средний квадрат тока. . . . . . . . . . . . . . . . . .	277
9.3.3.1.Режим эмиссии отдельных частиц. . . . .	279
9.3.3.2.Режим поглощения эмитированных частиц	281
9.3.3.3.Режим двухчастичной эмиссии. . . . . . .	282
9.3.4.Дробовой шум двухчастичного источника. . . . . . .	287
9.3.4.1.Режим эмиссии отдельных частиц. . . . .	288
9.3.4.2.Режим поглощения эмитированных частиц	289
9.3.4.3.Режим двухчастичной эмиссии. . . . . . .	289
9.4.Мезоскопический электронный коллайдер. . . . . . . . . .	291
9.4.1.Эффект подавление дробового шума. . . . . . . . .	293
9.4.2.Вероятностная интерпретация. . . . . . . . . . . . .	296
9.4.2.1.Одночастичные вероятности. . . . . . . . .	297
9.4.2.2.Двухчастичные вероятности для нескорре-
лированных частиц. . . . . . . . . . . . . .	298
9.4.2.3.Двухчастичные вероятности для скоррели-
рованных частиц. . . . . . . . . . . . . . .	299
9.5.Столкновение флуктуирующих электронных потоков. . . .	301
9.5.1.Эффект подавление кросс-коррелятора тока. . . . .	302
9.5.2.Вероятностная интерпретация. . . . . . . . . . . . .	305
9.5.2.1.Одночастичные вероятности. . . . . . . . .	305
9.5.2.2.Двухчастичные вероятности для нескорре-
лированных частиц. . . . . . . . . . . . . .	306
9.5.2.3.Двухчастичные вероятности для скоррели-
рованных частиц. . . . . . . . . . . . . . .	306
9.6.Двухчастичный интерференционный эффект. . . . . . . . .	308
9.6.1.Модель и определения для используемых величин. .	309

7

Содержание

9.6.2.Элементы матрицы рассеяния. . . . . . . . . . . . .	315
9.6.3.Кросс-коррелятор тока. . . . . . . . . . . . . . . . .	317
9.6.3.1.Частичные вклады. . . . . . . . . . . . . .	317
9.6.3.2.Суммарное выражение и его анализ. . . . .	324
9.6.3.3.Зависящий от магнитного потока коррелятор	325
Рекомендуемая литература	329
Список иллюстраций	341

8

Предисловие

Физика субмикронных и наноскопических объектов бурно развивается в последние десятилетия . Прогресс в этой области физики конденсированного состояния обусловил возможность создания твердотельных структур, позволяющих манипулировать отдельными электронами.Таки е устройства являются основой зарождающейся когерентной квантовой электроники.

В настоящем учебном пособии представлена теория транспортных явлений в фазово-когерентных,мезоскопических,системах , основанная на подходе,который в литературе называется подходом Ланда уэра- Бьюттикера(Landauer-B uttiker)¨ .Основа этого подхода состоит в том,что процесс протекания тока рассматривается как процесс рассеяния.Мезоскопический образец соединен с макроскопическими контактами,выполняющими роль электронных резервуаров.При низких температур ах электрон, двигаясь из одного резервуара через образец в другой резервуар,сохраняет фазовую когерентность,что позволяет описать его взаимоде йствие с образцом с помощью эффективного потенциала.Электрон,рассеива ясь на этом потенциале,либо отражается в тот резервуар из которого он п ришел,либо проходит в другой резервуар и,тем самым,вносит вклад в то к.В рамках рассматриваемого подхода центральным объектом,харак теризующим

транспортные свойства образца,является его матрица рассе яния ˆ.

S

Описан как стационарный,так и нестационарный режимы квант ового транспорта заряда и энергии.Наряду с током рассмотрены его флуктуации, обусловленные влиянием температуры,тепловые флуктуации , и дискрет - ностью носителей тока,дробовые флуктуации.В случае,когд а параметры образца изменяются периодически во времени,его свойства о писывают-

ся матрицей рассеяния Флоке ˆ , которая учитывает возможность измене -

SF

ния энергии электрона при взаимодействии с динамическим рассеивателем. Изучена связь матрицы рассеяния Флоке с матрицей рассеяния стационарного образца в случае медленного изменения параметров образца.Изложен

метод аналитического вычисления матрицы ˆ для точечного рассеивателя

SF

и системы точечных рассеивателей . Представлена теория эффекта квантового насоса,состоящего в генерирования постоянного тока д инамическим

9

Предисловие

рассеивателем.Рассмотрены флуктуации тока,переменный т ок и энергетика квантового насоса.В качестве приложения рассмотрен п ериодически действующий мезоскопический одночастичный эмитер.Показ ано,что дробовой шум,создаваемый частицами при рассеянии на квантово м точечном контакте,является квантованным и пропорционален числу эл ектронов и дырок,эмитированных в течение одного периода.Если два так ие эмитера расположены по разные стороны от точечного контакта,то они вносят аддитивный вклад в шум,за исключением того случая,когда они с инхронизированы и эмитируют частицы одного сорта,электроны или ды рки,одновременно.В таком случае дробовой шум исчезает,что обуслов лено возникновением квантово-статистических,фермиевских,корреля ций между электронами,соответственно,дырками,сталкивающимися в кван товом точечном контакте.Показано также,что возможно возникновение д вухчастичных корреляций даже в том случае,когда частицы непосредств енно не сталкиваются.Для этого необходимо наличие двух интерферометр ов,обеспечивающих существование нескольких альтернативных двухчастичных траекторий.Наличие или отсутствие двухчастичных корреляций регулируется путем изменения разности фаз потенциалов,управляющих раб отой источников,

Учебное пособие предназначено для научных работников,пре подавателей и студентов старших курсов,специализирующихся в обл асти физики конденсированного состояния,микроэлектроники и наноф изики.Необходимо знание основ квантовой механики и знакомство со статистической физики.

10

Глава1.

Формализм Ландауэра-Бьюттикера

ПОДХОД Ландауэра-Бьюттикера[ 1, 2, 3, 4, 5, 6] к транспортным явле - ниям в мезоскопических[ 7, 8] проводящих системах состоит в том , что процесс прохождения электронов через такие системы рассматривается как процесс рассеяния.Мезоскопическая система предполагает ся соединенной с макроскопическими контактами , которые выполняют роль электронных резервуаров и служат источником равновесных частиц.После рассеяния электроны возвращаются в тот же самый или уходят в другой контакт.Таким образом,задача вычисления таких макроскопических хар актеристик

образца как,например,электропроводность или теплопрово дность,сводится к решению квантовой задачи рассеяния,а вся информаци я о транс -

портных свойствах образца содержится в матрице рассеяния, ˆ. [9]

S

Этот подход является существенно одночастичным.Поэтому, мы пренебрегаем взаимодействием электронов с электронами(и дру гими квазичастицами)и используем уравнение Шредингера для бесспино вых частиц, в качестве основного уравнения в тех случаях , когда требуется определить квантово-механические амплитуды рассеяния.В рамках расс матриваемого метода,взаимодействие может быть добавлено в приближен ии среднего поля.

1.1.Матрица рассеяния

Согласно квантовой механике электрон характеризуется волновой функцией Ψ(t, r), зависящей от времени t и координат r. При этом гово - рят,что электрон находится в состоянии,описываемом волно вой функцией Ψ(t, r). Если известна волновая функция налетающей частицы ,Ψ(in), то , решая уравнение Шредингера,можно определить волновую фун кцию для рассеянной частицы, Ψ(out).

В принципе можно приготовить исходную частицу в различных состоя-

11

1.Формализм Ландауэра-Бьюттикера

ниях Ψ(jin), поэтому естественно возникает вопрос , следует ли решать урав-

нение Шредингера для каждой Ψ(jin). Оказывается , что нет . Достаточно ре - шить задачу рассеяния для частицы,находящейся в одном из со стояний ψα(in), которые составляют полный ортонормированный базис , а затем,используя принцип суперпозиции,определить результат рассе яния для произвольного состояния налетающей частицы.

Как это сделать?Разложим волновую функцию налетающего эле ктрона Ψ(in), в ряд по функциям ψα(in),

!
Ψ(in) = aα ψα(in) ,	(1.1)

α

а искомую волновую функцию рассеяного электрона Ψ(out) разложим в ряд по набору базисных состояний ψα(out),

Ψ(out) =	!
	bβ ψ(out) .	(1.2)
	β

β

Набор функций ψα(in) и ψβ(out) составляет полный базис по которому можно разложить произвольное состояние частицы,возможно вкл ючающее как падающую,так и отраженную волны.

Задача состоит в определении коэффициентов bβ по заданному набору коэффициентов aα. Вначале рассмотрим вспомогательную задачу . А имен - но,рассмотрим рассеяние частицы,находящейся в специальн о приготов -

ленном состоянии, Ψ(1in) = ψ1(in). Для выбранного состояния коэффициенты в разложении (1.1) имеют следующий вид :(1, 0, 0, . . .). Решение данной за - дачи рассеяния представим в виде ряда( 1.2) с коэффициентами , которые мы обозначим как Sβ1,

	!
Ψ1(out)	= Sβ1 ψβ(out) .	(1.3)

β

Коэффициент Sβ1 представляет собой квантово-механическую амплитуду перехода частицы из начального состояния ψ1(in) в конечное состояние ψβ(out).

12

1.1.Матрица рассеяния

Заметим,что если амплитуда исходной волны изменится на мно житель A, то и амплитуда рассеянной волны изменится на этот же множитель,

	Ψ1(out)	!
Ψ1(in) = A ψ1(in)		= A Sβ1 ψβ(out) .	(1.4)

β

Аналогично,решая задачу рассеяния для другого исходного с остояния Ψ(γin) = ψγ(in), определим коэффициенты Sβγ,

!
Ψγ(out) = Sβγ ψβ(out) .	(1.5)

β

Знание коэффициентов Sαβ позволяет решить задачу рассеяния частицы,находящейся в произвольном исходном состоянии.Формал ьная процедура определения волновой функции рассеянного состояния базируется на принципе суперпозиции и выглядит следующим образом.

1.Раскладываем исходную волновую функцию в ряд по функциям ψα(in), выражение( 1.1).

2.Волновую функцию рассеянного состояния Ψ(out) представляем в ви-

де суммы вкладов Ψ(αout), возникающих от рассеяния частичных исходных волн Ψ(αin) = aα ψα(in),

			Ψ(out) =		Ψα(out),
					α
					"	(1.6)
		Ψα(out) = aα			"
					Sβα ψβ(out) .
					β
3.Определяем коэффициенты bβ для искомого рассеянного состояния,
"	"	Sβα ψβ(out)	"
Ψ(out) =	aα		≡ bβ ψβ(out), где
α	β		β	!
						(1.7)
			bβ =		Sβα aα .

α

Уравнение( 1.7) решает поставленную задачу , а именно , выражает ко - эффициенты bβ, определяющие волновую функцию рассеянной частицы ,

13

1.Формализм Ландауэра-Бьюттикера

через коэффициенты aα, определяющие волновую функцию исходной ча - стицы.Величины Sβα, входящие в уравнение (1.7),удобно рассматривать

	ˆ
как элементы некоторой матрицы S, которую называют матрицей рассея-
ния.
Если коэффициенты aα и bβ представить в виде вектор-столбцов,
b1		a1
.		.		(1.8)
ˆb = b2	,	aˆ = a2	,

то соотношение между этими коэффициентами можно записать в компакт-

ном виде,
ˆ	ˆ	(1.9)
b = Saˆ .

Как уже отмечалось,элементы матрицы рассеяния Sαβ представляют собой квантово-механические амплитуды перехода(рассеян ия)частицы из состояния ψβ(in) в состояние ψα(out). Следует обратить внимание на то , что по - рядок индексов является важным.Мы ввели эти индексы так,чт о первый индекс(для элемента Sαβ это индекс α) соответствует конечному состоя - нию,а второй индекс соответствует начальному состоянию.

1.1.1.Свойства матрицы рассеяния

Исходя из общих физических принципов можно показать,что ма трица рассеяния не может быть произвольной и должна обладать вполне определенными свойствами.

1.1.1.1.Свойство унитарности

Сохранение числа частиц при рассеянии требует,чтобы матри ца рассеяния была унитарной,

ˆ† ˆ ˆ ˆ† ˆ (1.10)

S S = SS = I .

Здесь ˆ - единичная матрица . Ее диагональные элементы равны единице,а

I

все недиагональные элементы равны нулю,

14

1.1.Матрица рассеяния

Iˆ =		1 0 0 . . .	.	(1.11)
		0 1 0 . . .
		0 0.1. .. . .

Сопряженная матрица ˆ† получается из матрицы ˆ транспонированием

S S

(обозначаемым верхним индексом T ) и комплексным сопряжением ( обо -

			ˆ		ˆT			ˆ
значаемым верхним индексом		),	S† = )ˆ				*
		1.10)		+	S†	,		+	,
матриц связаны следующим образом,							αβ = S βα, поэтому в разверну -
том виде условие унитарности(			гласит ,
Nr
!		Sαβ Sαγ			= δβγ ,					(1.12)
α=1
Nr
!
		Sαβ Sδβ			= δαδ .					(1.13)

β=1

Для доказательство свойства унитарности,например в случа е,когда волновая функция нормирована и соответствует единичной частице,мы используем тот факт,что интеграл по всему пространству от ква драта модуля волновой функции равен единице.Применяя это требование к исходной волновой функции и к рассеянной,запишем,

ˆ d3r |Ψ(in)|2 = ˆ d3r |Ψ(out)|2 = 1 .

(1.14)

Далее используем разложения( 1.1) и (1.2).Например,для Ψ(in) получаем,

15

1.Формализм Ландауэра-Бьюттикера

´ d3r |Ψ(in)|2 =		´ d3r α	aα ψα(in)	- β	aβ	ψβ(in).
		"		"
""	aα aβ ´ d3r ψα(in) )ψβ(in)*			""		aα aβ δαβ
= α β				= α β

= "|aα|2 = 1 .

α

Здесь мы учли,что функции ψα(in) – ортонормированы,

ˆ	)	*
	d3r ψα(in) ψβ(in)	= δαβ ,

(1.15)

(1.16)

где δαβ – символ Кронеккера,равный единице для совпадающих индексо в, и,равный нулю для не совпадающих индексов,

δαβ =	1 ,	α = β ,	(1.17)
	0 ,	α = β .
		%
Аналогично для Ψ(out) находим,
!	|bα|2 = 1 .		(1.18)
α
Таким образом,из выражений(	1.15) и (1.18) следует ,

!!

|aα|2 =

|bα|2 .

(1.19)

αα

Используя представление коэффициентов aα и bα в виде вектор -

столбцов и ˆ, можем записать , aˆ b

16

1.1.Матрица рассеяния

" |aα|2 = aˆ† aˆ ,

α

" 2 ˆ† ˆ

(1.20)

|bα| = b b .

α

Далее,учитывая,что ˆ ˆ и,потому ˆ† † ˆ†, окончательно получим , b = S aˆ b = aˆ S

ˆ† ˆ † ˆ† ˆ † (1.21) b b = aˆ S S aˆ = aˆ aˆ .

Из последнего равенства следует требуемое соотношение( 1.10).

Следует заметить,что для частиц с непрерывным спектром,ко торые мы будем рассматривать,волновая функция нормируется не на единицу,а на дельта-функцию Дирака.В таком случае более естественно й является постановка задачи рассеяния при условии фиксированной плотностью потока падающих частиц.Так,например,плоская волна eikx соответствует потоку частиц с интенсивностью v = !k/m, а не единичной частице . Сохра - нение заряда в таком случае(в стационарных условиях)предп олагает сохранение(постоянного)тока.Поэтому удобно выбрать базис ные функции нормализованными на единичный поток,смотри,например, [ 10, 5].Тогда мы

можем сформулировать следующее:	ˆ
ˆ
Уравнение( 1.9)определяет матрицу рассеяния S	если вектора b и aˆ

вычислены с использованием базисных функций,которые норм ированы на единичный поток.

Квадрат модуля элемента матрицы рассеяния определяет плотность потока рассеянных частиц,при условии,что плотность потока пад ающих частиц равна единице.Следовательно,унитарность матрицы рассея ния отражает сохранение потока частиц.

1.1.1.2.Свойства,вытекающие из микрообратимости движен ия

Микрообратимость состоит в том,что уравнения движения час тицы обладают определенной симметрией,связанной с изменением направления времени.Ни классическая механика,ни квантовая механика н е делают раз - личия между движением во времени в одну и в другую сторону.

17

1.Формализм Ландауэра-Бьюттикера

Если изменить направление времени на противоположное, t → −t, и одновременно изменить направление скорости частицы на противоположное, v → −v, то уравнения классической механики предсказывают , что частица будет двигаться вдоль той же самой траектории,но в обр атном направлении.В рамках теории рассеяния изменение движения на противоположное означает,что рассеянная частица становится падающ ей,а падаю- щая-рассеянной.

В квантовой механике говорят не о траектории движения , а о состоянии частицы.Кроме того дополнительное усложнение возника ет от того,что волновая функция является комплекснозначной функцией.Дл я того , чтобы проанализировать микрообратимость в квантовой механике[ 11],рассмотрим уравнение Шредингера,

	i!	∂Ψ		= HΨ ,	(1.22)
		∂t

где H – оператор Гамильтона,зависящий от импульса частицы.При из - менении направления импульса на противоположное,гамильт ониан не изменяется, H() = H(−). Однако , при изменении времени на противополож - ное изменяется знак в левой части уравнения( 1.22).Если же одновременно с инверсией времени перейти к комплексно сопряженному уравнению и учесть,что оператор Гамильтона является эрмитовым операт ором, H = H, то полученное уравнение для комплексно сопряженное волновой функции Ψ (−t) будет совпадать с исходным уравнением для функции Ψ(t),

) *
∂ Ψ
i! ∂(−t) = H)Ψ * .	(1.23)

Отсюда видно,что,если эволюция в прямом направлении време ни в квантовой механике описывается волновой функцией Ψ(t), то эволюция в обрат - ном направлении времени описывается комплексно сопряженной функцией Ψ (−t). В рамках теории рассеяния микрообратимость квантовой механики означает,что,если падающая частица находится в состоян ии Ψ(in)(t), а рассеянная частица-в состоянии Ψ(out)(t), то при изменении направления

18

1.1.Матрица рассеяния

		падающая частица в состоянии			(out)
				)Ψ		(−t)*
времени на противоположное (in)
будет рассеяна в состояние		Ψ	(−t) .
Такая симметрия	уравнений движения определенным образом отража-
		)	*

ется в свойствах матрицы рассеяния.Для установления этих с войств рассмотрим процессы рассеяния в прямом и в инверсном времени.

Исходный

процесс:

Ψ(in)(t)

=

aα ψα(in)(t)

-

падающая

волна ,

α

Ψ

(out)

(t) =

(out)

(t)

"

bβ ψβ

- рассеянная волна . Соотношение между коэф -

β

фициентами a

и b

β

определяется уравнением( 1.9).

"α

bβ )ψβ(out)

(−t)*

Обращенный во времени процесс: )Ψ(out)(−t)*

=

β

- падающая волна ;)Ψ

(in)

(in)

(−t)*

"

(−t)*

=

α

aα )ψα

- рассеянная волна .

"

При инверсии времени и переходе к комплексно сопряженным величинам

базисные функции для налетающих и рассеянных состояний переходят друг

) *

в друга , ψβ(out)(−t) = ψβ(in)(t), поэтому можно записать ,

)Ψ(out)(−t)* = " bβ ψβ(in)(t) ,

β

(1.24)

) * "

Ψ(in)(−t) = aα ψα(out)(t) .

α

Поскольку гамильтониан и наборы базисных функций остались без изменения,то и матрица рассеяния осталась прежней.Следоват ельно,коэффициенты aα и bβ в уравнениях (1.24) связаны между собой также , как и коэффициенты bβ и aα в уравнениях (1.1) и (1.2),

aˆ = Sˆ ˆb .		(1.25)
Таким образом,наборы коэффициентов	ˆ	должны удовлетворять
	aˆ и b

двум уравнениям, (1.9) и (1.25).Из совместимости этих уравнений мы мо-

жем сделать искомое заключение о свойствах матрицы рассеяния ˆ. Так ,

S

19

1.Формализм Ландауэра-Бьюттикера

ˆ
выражая в уравнении( 1.9) коэффициенты aˆ через b, получаем ,
aˆ = Sˆ−1ˆb ,	(1.26)
где Sˆ−1 матрица обратная матрице рассеяния, SSˆ ˆ−1	= Sˆ−1Sˆ = Iˆ. Срав -

нивая полученное уравнение( 1.26) с уравнением (1.25),заключаем,что

ˆ ˆ−1. Далее , из условия унитарности матрицы рассеяния ,1(.10),сле-

S = S

дует,что обратная ей матрица совпадает с сопряженной,

Sˆ†Sˆ = Iˆ			Sˆ† = Sˆ−1 .	(1.27)
Sˆ−1Sˆ = Iˆ

Окончательно заключаем,что требование микрообратимости приводит к тому,что матрица рассеяния инвариантна относительно опер ации транспонирования.Или другими словами,ее матричные элементы си мметричны относительно перестановки индексов

ˆ ˆT	Sαβ = Sβα .	(1.28)
S = S

Наличие магнитного поля с напряженностью H и в классической фи - зике,и в квантовой физике слегка видоизменяет условие обра тимости движения.При изменении направления времени и скорости на прот ивоположное необходимо дополнительно изменить направление магнитного поля на противоположное, H → −H, поскольку сила , действующая на заряд в маг - нитном поле(сила Лоренца)зависит от произведения скорост и и напряжен - ности магнитного поля.В случае квантовой механики необход имость такой замены хорошо видна из выражения для(собственных значений ) гамильто - ниана свободной частицы с зарядом e и массой m, движущейся вдоль оси x,

H = (px − eAx)2 ,

2m

20

1.2.Оператор тока

где Ax - проекция векторного потенциала на ось x. Напомним , что вектор - ный потенциал A определяет напряженность магнитного поля H следующим образом, H = rotA. Изменяя импульс частицы на противоположный , px → −px, необходимо дополнительно изменить величину магнитного поля (векторного потенциала)на противоположную, Ax → −Ax, чтобы гамиль - тониан не изменился.

Таким образом,при наличии магнитного поля условие( 1.28) принимает следующий вид, [5]

ˆ	ˆT	(−H) Sαβ(H) = Sβα(−H) .	(1.29)
S(H) = S

В частности , мы видим , что амплитуда отраженияα, = β, является четной функцией магнитного поля.

Следует заметить,что при наличии у частицы спина условие ми крообратимости и,соответственно,симметрия матрицы рассеяния видоизменяется.Однако мы на этом вопросе останавливаться не будем.

1.2.Оператор тока

Далее мы перейдем к рассмотрению того,как формализм матриц ы рас - сеяния может быть применен к рассмотрению транспортных свойств мезоскопических образцов.

Прежде всего,следует отметить,что применение формализма матрицы рассеяния предполагает использование,так называемого, одноэлектронного приближения. Это приближение состоит в том , что отдельные элек - троны рассматриваются как независимые частицы,взаимодей ствие которых с другими электронами,примесями,другими квазичастиц ами в твердом теле,внешними полями,и прочее учитывается с помощью эффек тивной потенциальной энергии Ueff (t, r) в поле которой движется рассматриваемый электрон.Такое приближение хорошо зарекомендовало себя в физике твердого тела,с той лишь оговоркой,что электрон в твердом теле и меет массу m , которая в общем случае может отличаться от массы свободного элек - трона me. Заметим , что одноэлектронное приближение не позволяет опи-

21

1.Формализм Ландауэра-Бьюттикера

α = 3, · · · , Nr − 1

α = Nr	ˆ
	S

Σ

α = 2

α = 1

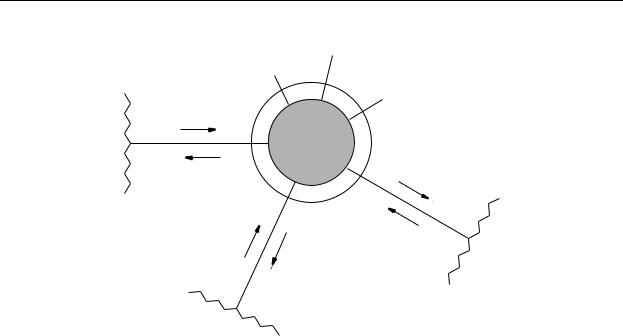
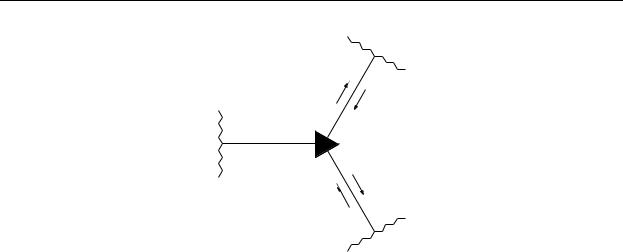
Рис. 1.1.Мезоскопический образец с матрицей рассеяния	ˆ	. Индекс α =
	S

1, 2, . . . , Nr нумерует электронные резервуары.Стрелки направленные к о б- разцу(от образца)показывают направление движения налета ющих(рассеянных)электронов.Поток электронов вычисляется на поверх ности Σ, пока - занной штриховой линией.

сать довольно интересные многочастичные эффекты.Однако, и это следу - ет подчеркнуть,такое приближение позволяет довольно прос то и наглядно описать физику явлений на качественном,а во многих случаях и на количе - ственном уровне.

Рассмотрим мезоскопический образец,который соединен с не сколькими, Nr, контактами , играющими роль электронных резервуаров , Рис. 1.1. Электрон,двигаясь из резервуара по направлению к образцу, попадет в образец и будет рассеиваться примесями в образце,стенками,о граничивающими образец и тому подобное.Однако в конце концов электро н поки - нет образец и уйдет в какой-то из резервуаров.Для того,чтоб ы вычислить ток,который протекает между образцом и резервуарами,нет н еобходимости следить за тем,что происходит с электроном,когда он нах одится в образце.Достаточно рассмотреть процессы прихода электроно в в образец и процессы ухода электронов из образца.Для этого окружим обр азец вооб-

22

ψα(out)

1.2.Оператор тока

ражаемой поверхностью Σ (смотри рис. 1.1) и вычислим поток электронов , пересекающий эту поверхность,по направлению к образцу,и п оток электронов,пересекающий поверхность Σ, по направлению от образца . При та - ком подходе мы,фактически,имеем дело с задачей рассеяния: Электроны движущиеся по направлению к образцу-это налетающие (in) частицы,а электроны движущиеся по направлению от образца-это рассея нные (out) частицы.

Подчеркнем,что мы будем рассматривать только упругое,то е сть,сохраняющее энергию,рассеяние,предполагая,что в образце э лектрон не испытывает неупругих столкновений.Это предположение накла дывает определенные требования на размер образца L и температуру T , Lϕ(T ) ( L, где Lϕ - длина сбоя фазы электрона .

Удобно выбрать волновые функции электрона в проводниках,с оединяющих образец с резервуарами,в качестве базисных функций дл я определе - ния элементов матрицы рассеяния.Эти волновые функции могу т быть пред - ставлены в виде произведения поперечных и продольных составляющих. Поперечные составляющие определяются той подзоной к которой принадлежит рассматриваемый электрон.Во избежания излишнего ус ложнения формул,мы будем полагать,что в каждом проводнике имеется т олько одна проводящая подзона.Продольные же волновые функции выбе рем в виде плоских волн,бегущих по направлению к образцу(волновое число −k) или от образца(волновое число k).При этом первые составляют базис для

налетающих волн, ψα(in), а вторые составляют базис для рассеянных волн ,

.

Для вычисления тока,текущего между образцом и резервуарам и, мы воспользуемся формализмом вторичного квантования.Это т форма - лизм предполагает введение операторов рождения/уничтожения электрона в определенном квантовом состоянии.Для удобства мы буде м использо - вать различные обозначения для операторов,соответствующ их электронам, движущихся из резервуаров к образцу, -операторы aˆ†α(E)/aˆα(E), и рассе - янных электронов,которые движутся от образца к резервуара м, -опера-

торы ˆ† /ˆ . Оператор † рождает электрон в состоянии,описы- bα(E) bα(E) aˆα(E)

ваемом волновой функцией ψα(in)(E)/					,	а оператор ˆb†				(E) рождает
			!vα(E)
				(out)			5		α
электрон в состоянии с волновой	функцией					(E)/	!		vα(E). Множитель
		5		ψα

23

1.Формализм Ландауэра-Бьюттикера

5

1/ !vα(E) учитывает нормировку на единичный поток.Отметим,что индекс α помимо номера контакта,может включать номер поперечной по дзоны в этом контакте,направление спина электрона и другие ква нтовые числа.Введенные операторы удовлетворяют следующим антикомм утационным соотношениям,

aˆα† (E) aˆβ(E)) + aˆβ(E)) aˆα† (E) =						δαβ δ(E − E)) ,
							(1.30)
ˆ†	ˆ	)	ˆ	)	ˆ†	)	) .
bα(E) bβ(E			) + bβ(E		) bα(E) =	δαβ δ(E − E

Далее рассмотрим зависящие от времени t и координаты r полевые операторы,соответствующие электронам в проводнике α,

∞

ˆ √1 ˆ Ψα(t, r) =

2π

0

dE e−i	E	6aˆα(E)	(in)		E, r)
	! t		ψα	!v(α(E)
			5

+ ˆbα(E)	(out)(E, r)			7	,
	ψα	!vα(E)
	5

	1			∞		E	6aˆα† (E)	ψ(in) (E, r)
Ψˆ α†	(t, r) =	√		ˆ	dE ei	! t		α
			2π					5	!vα(E)
				0

				(1.31)
+ ˆbα† (E)	(out) (E, r)
	ψα	!vα(E)		7 .
	5

Здесь vα(E) = !kα(E)/m - скорость электрона в проводнике α; r = (x, r ), где x - координата вдоль проводника , аr - координата в поперечной плос - кости проводника.Отметим,что 1/(hvα(E)) - есть плотность состояний , (2π)−1dk/dE, электронов в одномерном проводнике α.

Вышеприведенные операторы определяют оператор тока ˆ , протека -

Iα

ющего через поперечное сечение проводника α, следующим образом ,

Iˆα(t, x) =	i!e	ˆ	dr 8	∂Ψˆ α† (t, r)		Ψˆ α(t, r) − Ψˆ α† (t,
	2m			∂x

	ˆ	9 .
r)	∂Ψα(t, r)		(1.32)
	∂x

Здесь ток,направленный от рассеивателя,считается положи тельным.

24

E−E!

!

1.2.Оператор тока

Далее мы запишем,

ψ(in)(E, r) = ξE(r ) e−ik(E) x ,

(1.33)

ψ(out)(E, r) = ξE(r ) eik(E) x ,

иучтем , что поперечные волновые функции нормированы ,

ˆ

dr |ξE(r )|2 = 1 .

(1.34)

В дальнейшем мы будем интересоваться током при напряжениях, которые существенно меньше,чем энергии Ферми µ0, поэтому во всех последующих формулах основной вклад будет происходить от энергий удовлетворяющих следующему условию,

|E − E)| - E µ0 .

(1.35)

Последнее условие позволяет существенно упростить выражение для опе-

ратора тока,положив v(E)	≈	v(E)), k(E)		≈	k(E)). Кроме того , в пределах
одной подзоны ξE = ξE!. Отметим , что функцииξE и ξE!, относящиеся к
разным подзонам,ортогональны,			´ dr ξE(r ))ξE!(r )* = 0, что позволя -

ет представить полный ток в виде суммы токов,переносимых эл ектронами отдельной подзоны.Напомним,что мы рассматриваем проводн ики с одной проводящей подзоной.

Подставляя( 1.31) в (1.32) и учитывая (1.35),получаем,

ˆ i!e ˜ ) ei t ´ 2

Iα(t, x) = 2m dE dE hvα(E) dr |ξE,α(r )|

6 : ;- .

ˆ ˆ

× ∂∂x aˆ†α(E)eikα(E)x + b†α(E)e−ikα(E)x aˆα(E))e−ikα(E)x + bα(E))eikα(E)x

- . : ;7

ˆ ˆ

− aˆ†α(E)eikα(E)x + b†α(E)e−ikα(E)x ∂∂x aˆα(E))e−ikα(E)x + bα(E))eikα(E)x .

25

1.Формализм Ландауэра-Бьюттикера

Дифференцируя по x и приводя подобные члены , окончательно получим вы - ражение для оператора тока в следующем виде[ 5],

	h	<		−	=
Iˆα(t) =	e	¨ dE dE) eiE−!E! t ˆbα†	(E) ˆbα(E))		aˆα† (E) aˆα(E)) .	(1.36)
В дальнейшем мы будем использовать полученное выражения для вы -
числения тока		ˆ
		Iα = 0Iα1 протекающего через образец.При этом нам необ-

ходимо будет выполнить квантово-механическое и статистическое усред-

нение . . .	1	произведений операторов aˆ†aˆ и ˆb†ˆb по состоянию налетающих
0
электронов.

Операторы рождения и уничтожения aˆ†α и aˆα соответствуют частицам, движущимся из резервуара к образцу и,потому,еще не взаимод ействовавшим с рассеивателем.Следовательно,эти операторы соответ ствуют частицам резервуара.Мы полагаем,что присутствие мезоскопичес кого образца не оказывает существенного влияния на макроскопические резервуары, которые остаются в состоянии термодинамического равновесия.Кроме того,мы полагаем,что электронные состояния в различных резе рвуарах не скоррелированы между собой.С учетом этих предположений,к вантовостатистические средние от произведения a−операторов,

0aˆ†α(E) aˆβ(E))1 = δαβ δ(E − E)) fα(E) ,

> ? (1.37)

0aˆα(E) aˆ†β(E))1 = δαβ δ(E − E)) 1 − fα(E) ,

выражаются через равновесные функции распределения fα(E) соответствующих резервуаров,которые в случае электронов являютс я функциями распределения Ферми[ 12]:

fα(E) =	1	(1.38)
	E−µα .

1 + e kBTα

Здесь kB - постоянная Больцмана ;µα, Tα - химический потенциал и темпе - ратура резервуара α.

26

1.3.Постоянный ток и функция распределения

Операторы ˆ† , ˆ соответствуют рассеянным частицам,которые bα bα

являются неравновесными частицами.Для вычисления кванто востатистического среднего необходимо выразить эти операторы через операторы налетающих частиц.Для этого рассмотрим полевой оператор,

		ˆ (in)		,
соответствующий падающей волне, Ψ
		!				(in)
ˆ		Nr
	(in)				ψα
Ψ		=	aˆα		√	!vα		,
		α=1
								ˆ	(out)	,
и полевой оператор , соответствующий рассеянной волне ,Ψ
		Nr			(out)
ˆ (out)		!	ˆ		5
					ψβ
Ψ		=	bβ				!vβ	.
		β=1

Эти выражения вполне аналогичны выражениям( 1.1) и (1.2),за исключением того,что в рассматриваемом случае коэффициенты разло жения представляют собой операторы,а не числа.Таким образом,каждый из операто-

ров ˆ выражается через все операторы при помощи элементов матрицы bβ aˆα

рассеяния,представляющей собой Nr×Nr матрицу,аналогично выражению (1.9),которое в развернутом виде есть, [ 5]

	Nr		Nr
ˆ	!	ˆ†	!	†
bα =	Sαβ aˆβ ,	bα =	Sαβ aˆβ .
	β=1		β=1

Уравнения( 1.36) - (1.39) составляют основу формализма матрицы рассеяния в мезоскопике.

1.3.Постоянный ток и функция распределения

Вычислим ток Iα,

ˆ	(1.40)
Iα = 0Iα1,

27

1.Формализм Ландауэра-Бьюттикера

протекающий в проводнике α, под действием постоянной во времени раз - ности потенциалов Vαβ = Vα − Vβ, приложенной между резервуарами . То есть,мы будем полагать,что различные резервуары имеют раз личные постоянные во времени химпотенциалы,

			µα = µ0 + eVα .				(1.41)
ˆ			определяется выражением( 1.36).Выполняя
Оператор тока Iα(t)
квантово-статистическое усреднение в выражении( 1.40),получим,
	h		<		−	=
Iα =	e		ˆ dE	fα(out)(E)		fα(in)(E) ,	(1.42)

где мы ввели функции распределения для электронов летящих из резервуа - ра к образцу, fα(in), и от образца к резервуару ,fα(out),

0aˆ†α(E) aˆα(E))1 = δ(E − E)) fα(in)(E) ,

						(1.43)
ˆb†	(E) ˆb	(E))	1	= δ(E	−	E)) fα(out)(E) .
0 α	α

Физический смысл введенных функций распределения состоит в следую - щем:величина dEh fα(in/out)(E) представляет собой среднее число частиц в интервале энергий dE вблизи энергии E пересекающих в единицу времени поперечное сечение контакта α по направлению к образцу/от образца.Ток Iα равен произведению заряда одной частицы, e, и разности потоков частиц .

Согласно уравнению( 1.37),функция распределения для налетающих электронов равна функции распределения Ферми для соответствующего резервуара,

fα(in)(E) = fα(E) .

(1.44)

Для вычисления функции распределения рассеянных электронов f(out)(E) воспользуемся уравнениями( 1.39) и (1.37) и получим ,

28

1.3.Постоянный ток и функция распределения

δ(E	−	E)) fα(out)(E)			ˆb† (E) ˆb		(E))		1
		"		≡ 0 α		α
β"
Nr		Nr	(E) S		(E)) aˆ†			(E))
=		S				(E) aˆ				1
		αβ	αγ		0 β		γ
=1 γ=1
β"		"
Nr		Nr
=		Sαβ(E) Sαγ(E)) δ(E − E)) δβγ fβ(E) .

=1 γ=1

Следовательно,функция распределения f(out)(E) для покидающих образец электронов зависит от фермиевских функций распределения всех резервуаров fβ(E),

Nr
!
fα(out)(E) = |Sαβ(E)|2 fβ(E) .	(1.45)

β=1

Если все резервуары имеют одинаковые потенциалы и температуры, fβ = f0, β, то функция распределения для рассеянных электронов будет равновесной фермиевской функцией распределения.Чтобы по казать это, воспользуемся условием унитарности матрицы рассеяния,

		Nr
ˆ ˆ†	ˆ	!	2	(1.46)
SS	= I		|Sαβ(E)| = 1 ,

β=1

и получим ,fα(out)(E) = f0(E) "Nr |Sαβ(E)|2 = f0(E). Если же между резер -

β=1

вуарами существует разность потенциалов и/или температур, то рассеян - ные электроны будут описываться неравновесной функцией распределения,

рис. 1.2.

Подставляя выражения( 1.44) и (1.45) в выражение для тока , (1.42) и используя выражение( 1.46),окончательно находим,

Iα = e ˆ			dE	Nr	Sαβ(E) 2		fβ(E)		fα(E) .	(1.47)
				!		<			=
	h			β=1 |	|			−

29

1.Формализм Ландауэра-Бьюттикера

f1(out)
1
µ1	µ2	E

Рис. 1.2.Функция распределения электронов,рассеянных в к онтакт α = 1. Высота ступени равна |S12|2. Образец соединен с дву - мя резервуарами,находящимися при нулевой температуре, T1 = T2 = 0, и имеющими химические потенциалы µ1 и µ2.

Из полученного выражения видно,что ток,текущий в проводни ке α, зависит от разности фермиевских функций распределения резервуаров, умноженной на квадрат модуля матричного элемента,описыва ющего рассеяние электрона между этими резервуарами.Если все резерв уары имеют одинаковые потенциалы и температуры,то ток равен нулю.В пр отивном случае через образец может течь ток.

1.3.1.Сохранение постоянного тока

Убедимся,что полученное выражение( 1.47) удовлетворяет условию сохранения постоянного тока,

!Nr

Iα = 0 ,

(1.48)

α=1

которое является следствием того,что заряд не может неогра ниченно накапливаться в мезоскопическом образце.Полученное выраже ние гласит, что сумма токов,текущих во всех проводниках,соединяющий о бразец с резервуарами,равна нулю.Во избежание недоразумений напо мним,что в каждом из проводников α положительное направление выбрано от образца к соответствующему резервуару.Ток берется со знаком +/− , если он

30

1.3.Постоянный ток и функция распределения

направлен от образца/к образцу .

Прежде всего получим уравнение( 1.48).Для этого проинтегрируем уравнение непрерывности для электрического заряда,

	div j +	∂ρ		= 0 ,	(1.49)
		∂t

(где j - вектор плотности тока ;ρ - объемная плотность заряда ) по объему , охватываемому поверхностью Σ (смотри Рис. 1.1).Преобразуя объемный интеграл от дивергенции плотности тока в поверхностный интеграл от плотности тока,и,учитывая,что ток течет только по проводникам , получаем ,

Nr
!	∂Q		(1.50)
Iα(t) +		= 0 .
α=1	∂t

Здесь Q - заряд образца В стационарном случае , когда по проводни - кам текут постоянные токи и заряд образца не изменяется,ура внение (1.50) совпадает с уравнением (1.48).В нестационарном случае усредним уравнение( 1.50) по времени . Вводя определение постоянного токаIα =

limT→∞ 1 ´ T dt Iα(t) и предполагая , что заряд образца ограничен , снова по -

T 0

лучаем уравнение( 1.48) как следствие уравнения (1.50).

Теперь проверим удовлетворяет ли условию сохранения постоянного тока полученное нами выражение( 1.47).Для этого рассмотрим сумму токов,текущих во всех проводниках,и покажем,что эта сумма,к ак и должно быть,равна нулю.При этом мы будем использовать условие уни тарности для матрицы рассеяния,записанное в форме,отличной от урав нения( 1.46),

	Nr
ˆ† ˆ ˆ	!	2	(1.51)
S S = I		|Sαβ(E)| = 1 .

α=1

Из выражения( 1.47) получаем ,

31

1.Формализм Ландауэра-Бьюттикера

"		" "
Nr		Nr Nr
α=1 Iα = he ´ dE α=1 β=1 |Sαβ(E)|2 <fβ(E) − fα(E)=					7
= he ´ dE6	"	"	"	"
	Nr	Nr	Nr	Nr
	β=1 fβ(E) α=1 |Sαβ(E)|2		− α=1 fα(E) β=1 |Sαβ(E)|2
		"	"
		Nr	Nr
= he ´ dE6β=1 fβ(E) − α=1 fα(E)7 = 0 .

Что и требовалось доказать.Таким образом,мы получили подт верждение тому,что,как уже упоминалось,унитарность матрицы рассея ния связана с сохранением тока при рассеянии.

Далее мы применим выражение( 1.47) для вычисления тока в некото - рых частных случаях.

1.3.2.Разность потенциалов

Пусть резервуары имеют различные потенциалы и одинаковые температуры,

µα = µ0 + eVα , eVα - µ0 ,

(1.52)

Tα = T0 , α .

При выполнении условия |eVα| - kBT0, можно разложить функции распределения в ряд по степеням малых потенциалов,

fα = f0 − eVα ∂∂fE0 + O(Vα2) ,

где f0 - фермиевская функция распределения с химпотенциалом µ0 и тем - пературой T0. Подставляя это разложение в (1.47),получим выражение для тока в следующем виде,

32

1.3.Постоянный ток и функция распределения

Nr	>	?
!			(1.53)
Iα =	Gαβ Vβ − Vα	,

β=1

где мы ввели элементы матрицы проводимости(матрицы кондак танса),

	ˆ	dE -−	∂f	.|Sαβ(E)|2 ,
Gαβ = G0			∂E0		(1.54)

где G0 = e2/h - квант кондактанса для бесспиновых электронов . C учетом спина электрона,вышеприведенная величина должна быть удв оена.

При температуре равной нулю, T0 = 0, производная от фермиевской функции распределения по энергии вырождается в δ−функцию Дирака,

−∂∂fE0 = δ(E − µ0) .

Это сводит интегрирование по энергии в( 1.54) к замене E → µ0 в подинте - гральном выражении,после чего выражение для кондактанса п риобретает исключительно простой вид, [5]

Gαβ = G0	@Sαβ(µ0)@2		,	(1.55)
	@	@
	@	@

Разумеется линейная зависимость между током и напряжением выдерживается лишь при относительно небольших напряжениях.Чем определяется величина напряжений при которых вольт-амперная характеристика становится нелинейной?Эта величина определяется харак тером зависимости элементов матрицы рассеяния Sαβ(E) от энергии.Для того,чтобы показать это,вычислим ток при нулевой температуре, T0 = 0, и конечных потенциалах, eVα =% 0. В этом случае мы не можем разложить фермиевскую функцию распределения в ряд по степеням напряжения,поэтом у выраже - ние для тока( 1.47) принимает следующий вид ,

33

1.Формализм Ландауэра-Бьюттикера

		µ0+eVβ
Iα =	G0	Nr	ˆ	dE	|	Sαβ(E) 2 .	(1.56)
	e	β=1	+eVα			|
		!µ0

Если величина Gαβ изменяется слабо в интервале энергий |eVβ − eVα|

вблизи энергии Ферми µ0, то мы можем вынести Sαβ(E) ≈ Sαβ(µ0) за знак интегрирования по энергии в( 1.56) и получим линейную зависимость тока

от напряжения,выражение( 1.53).

Если же нельзя пренебречь зависимостью от энергии величины Sαβ(E), то зависимость тока от напряжения становится нелинейной .В ка - честве примера рассмотрим образец с двумя контактами( α = 1, 2),проводимость которого определяется резонансным уровнем,распо ложенном при энергии E1 и имеющем полуширину %,

|S12(E)|2 =	%2	(1.57)
	(E − E1)2 + %2 .

Для простоты рассуждений положим E1 = µ0. Тогда , подставляя приведен - ное выражение в( 1.56),получим,что величина тока,протекающего через такой образец,будет равна,

e

eV

eV

I1 =

% 8arctg

-

2

. − arctg

-

1

.9.

(1.58)

h

%

%

В случае малых потенциалов ,|eV1|, |eV2|

- %, выполняется закон Ома ,

I12 = G0

V1 − V2

. В обратном случае ,|eV1|, |eV2|

( %, ток является нели -

нейной

+

,

I1

)

−

V2−

*

= ( %/h) V1−

1

1 . Таким образом мы

функцией потенциалов,

2

видим,что в рассматриваемом случае ширина резонанса % является характерным масштабом разделяющим линейный и нелинейный режимы протекания тока.

34

1.3.Постоянный ток и функция распределения

1.3.3.Разность температур

Различие в температурах резервуаров также может вызвать ток.Это, так называемый,термоэлектрический ток.Итак,пусть резер вуары имеют одинаковые потенциалы,но различные температуры,

µα = µ0 , α ,

(1.59)

Tα = T0 + Tα, Tα - T0 .

Раскладывая фермиевские функции в выражении( 1.47) в ряд по степеням

Tα,

fα = f0 + Tα ∂∂fT0 + O(Tα2 ) ,

и учитывая , что

∂f0	=	−	E − µ0 ∂f0			,
∂T			T0 ∂E

получаем выражение для термоэлектрического тока,текущег о в проводнике α, в следующем виде ,

Nr		>	?
!	Gαβ(T )			(1.60)
Iα =		Tβ − Tα	.

β=1

Здесь мы ввели термоэлектрический кондактанс,

G(T )	(E) =	π2e	kBT0	∂ |Sαβ(E)|2	.	(1.61)
αβ		3h		∂E

При получении этого выражения было использовано значение следующего интеграла,

35

1.Формализм Ландауэра-Бьюттикера

a

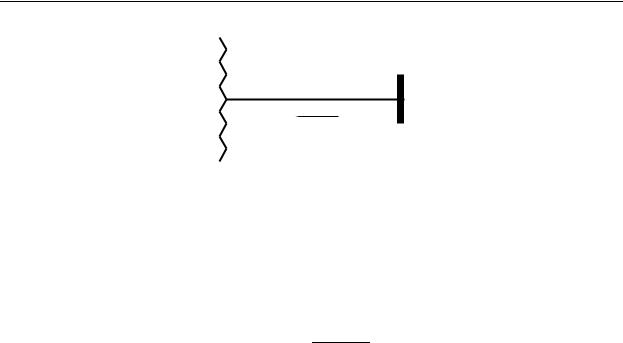
b

Рис. 1.3.Образец(черный прямоугольник)с одним каналом ра ссеяния. a – амплитуда налетающей волны, b – амплитуда отраженной волны.Волнистой линией обозначен резервуар электронов.

∞

E−µ

0

2

π

2

k T

dE

e B

0

E − µ0

=

kBT0 .

ˆ

)

1 + e

*

- kBT0 .

3

kBT0

0

E−µ0

2

Из выражения( 1.61) следует , что , если кондактанс образца не зависит от энергии, Gαβ(E) = const, то термоэлектрический ток отсутствует .

1.4.Примеры

Сейчас мы рассмотрим несколько примеров,иллюстрирующих т о,какой может быть матрица рассеяния и каков физический смысл ее элементов.Как мы уже говорили,матрица рассеяния имеет размернос ть Nr × Nr, где Nr - количество одномерных проводящих подзон во всех проводниках, соединяющих мезоскопический образец с резервуарами.Мы та кже будем говорить,что в задаче имеется Nr каналов рассеяния.

1.4.1.Матрица рассеяния с размерностью 1 × 1

Такая матрица рассеяния имеет всего один элемент S11 и описывает образец соединенный всего с одним резервуаром с помощью одномерного проводника,рис. 1.3. Например , это может быть обкладка мезоскопическо - го конденсатора.

36

1.4.Примеры

Для выяснения того,каким может быть этот элемент используе м усло - вие унитарности( 1.10),которое в данном случае,гласит, |S11|2 = 1. Откуда следует общий вид матрицы рассеяния с размерностью 1 × 1:

ˆ	iγ	,	(1.62)
S = e

где i - мнимая единица , аγ - действительное число .

Физически рассеяние в данном случае сводится к полному отражению падающей волны,поэтому этот матричный элемент называют- коэффициентом отражения. Вообще говоря , любой диагональный элементSαα матрицы рассеяния есть коэффициент отражения,поскольку о н определяет амплитуду и фазу волны,уходящей от рассеивателя в тот же рез ервуар α, из которого пришла падающая волна.

В рассматриваемом (1 × 1) случае амплитуда отраженной волны сов - падает с амплитудой падающей волны,а фаза отраженной волны изменяется на величину γ, которая зависит от свойств мезоскопического образца . Например,если отражение происходит от непроницаемого пот енциального барьера,то при отражении фаза волны изменяется на γ = π. Если же рассеивателем является мезоскопическое кольцо,то величи на γ будет изменяться в зависимости от величины захваченного магнитного потока Φ.

1.4.2.Матрица рассеяния с размерностью 2 × 2

Эта матрица имеет4элемента,каждый из которых,в общем случ ае,

является комплексным числом.Всего имеем8действительных	парамет-
ров.Однако,эти параметры не являются независимыми,поско	льку,уни-

тарность,выражение( 1.10),накладывает4условия на матричные элементы.Таким образом,всего остается4независимых параметра. В качестве таковых удобно выбрать следующие.

1)R = |S11|2 - вероятность отражения .

2)γ - фаза , определяющая эффективный заряд рассеивателяQ соглас-

но правилу сумм Фриделя, ˆ .[13]

Q = e/(2πi) ln(det S) = eγ/π

3) θ - фаза , характеризующая асимметрию между коэффициентами отражения в одном и во втором каналах рассеяния, θ = i ln (S11/S22) /2.

37

1.Формализм Ландауэра-Бьюттикера

a1

a2

b1 b2

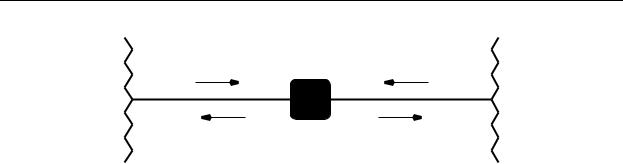
Рис. 1.4.Образец с двумя каналами рассеяния. aα (bα) – амплитуды налетающих(рассеянных)волн, α = 1, 2.

4) φ - фаза , характеризующая асимметрию между коэффициентами прохождения из одного контакта в другой и обратно, φ = i ln (S12/S21) /2. Эта фаза зависит от величины магнитного поля или внутреннего магнитно - го момента рассеивателя.

Общее выражение для матрицы рассеяния размерности 2 × 2, описы - вающий образец,соединенный с двумя резервуарами,рис. 1.4, имеет следу - ющий вид,

√

iθ

iφ

i√1 − R e−

Sˆ = eiγ

R e−

,

(1.63)

i√

eiφ √

eiθ

1 − R

R

Обратим внимание на то,что в рассматриваемом случае вероят ность отражения в обоих каналах рассеяния одинакова,

|S11|2 = |S22|2 = R .

(1.64)

Такое же равенство справедливо и для вероятностей прохождения из одного контакта в другой и обратно,

|S12|2 = |S21|2 .

(1.65)

Помимо этого,условие симметрии( 1.29) накладывает определенные ограничения на возможную зависимость параметров матрицы рассеяния от

38

1.4.Примеры

магнитного поля.Так,зависимости γ(H), R(H), и θ(H) должны быть четными функциями магнитного поля, X(H) = X(−H). А зависимость φ(H) должна быть нечетной, φ(H) = −φ(−H). Из последнего равенства непо - средственно следует,что в отсутствие магнитного поля, H = 0, величина φ = 0 и,следовательно,коэффициент прохождения не зависит от на правления движения,

S12(H = 0) = S21(H = 0) .

(1.66)

Обратим внимание на то,что более общее равенство, ( 1.65),выполняется и при наличии магнитного поля.

Из приведенных выше рассуждений следует,что кондактанс, G ≡ G12 = G21, проводника с двумя одномерными контактами является четной функцией магнитного поля,

G(H) = G(−H) .

(1.67)

Как мы покажем ниже,это свойство сохраняется и в случае обра зца с двумя квази-одномерными контактами.

Указанная симметрия( 1.67) в магнитном поле является следствием микрообратимости квантово-механических уравнений движения,которые справедливы в отсутствие неупругих или других сбивающих фазу волновой функции процессов.

1.4.3.Матрица рассеяния с размерностью 3 × 3

Такая матрица рассеяния описывает образец,соединенный с т ремя резервуарами,рис. 1.5. Она имеет уже довольно много , а именно , 9, независи - мых параметров,что делает затруднительным нахождение общ его вида этой матрицы.Обычно используют частные выражения для элементо в матрицы рассеяния.Например,следуя авторам работы[ 14],можно записать матрицу рассеяния,зависящую всего от одного вещественного параме тра ,,

39

1.Формализм Ландауэра-Бьюттикера

a3

b3 a1

b1 b2

a2

Рис. 1.5.Образец с тремя каналами рассеяния. aα (bα) – амплитуды налетающих(рассеянных)волн, α = 1, 2, 3.

( + b)

√

√

,

,

√,

b

a

Sˆ =

− a√

,

a

b

,

(1.68)

где параметр , может изменяться в следующих пределах, 0 ≤ ,

≤ 0.5,

√

√

a = (

1 − 2,

−1)/2 и b = (

1 − 2,

+1)/2. Параметр , характеризует степень

связи между контактом1и образцом.При

, = 0 контакт1полностью отсо-

единен от образца, S11 = −1, и электроны свободно проходят от контакта 2 в контакт 3 и обратно ,S32 = S23 = 1. Предел , = 0.5 соответствует безотражательной связи между образцом и первым контактом,то ест ь, S11 = 0.

Иногда,при решении уравнения Шредингера,в случае контакт а трех одномерных проводников,применяют так называемые граничн ые условия Гриффитса[ 15].Эти условия включают,во-первых,непрерывность волновой функции в точке контакта и,во-вторых,равенство нулю ли нейной комбинации производных волновой функции по координатам в точке контак - та,обеспечивающее сохранение тока.Такие условия соответ ствуют матрице рассеяния( 1.68) с параметром , = 4/9. Другие значения параметра , можно рассматривать как такие,которые соответствуют нали чию точечного туннельного барьера в месте контакта проводников.

Следует отметить,что в отличие от случая двух контактов,см отри

40

1.4.Примеры

(1.64),при наличии трех контактов вероятности отражения в разны х ка - налах рассеяния Rαα ≡ |Sαα|2, α = 1, 2 или 3, могут различаться . Кроме того,ток,текущий между двумя контактами,зависит не тольк о от вероят - ности прохождения между этими контактами Tαβ ≡ |Sαβ |2, α =% β, но и от вероятностей прохождения в третий контакт, Tγα и Tγβ, γ =% α,β .

1.4.4.Образец с двумя квази-одномерными проводниками

Покажем,что для мезоскопического образца с двумя контакта ми кондактанс есть четная функция магнитного поля.Ранее мы уж е пока - зали это,смотри( 1.67),для случая,когда образец соединен с контактами одномерными проводниками и,соответственно,матрица ра ссеяния есть 2 × 2 унитарная матрица.Сейчас мы обобщим этот результат на боле е общий случай,а именно,когда каждый из проводников являетс я квази - одномерным,то есть имеет несколько проводящих одномерных подзон. [16]

Пусть один проводник,назовем его левым проводником,имеет NL проводящих подзон,а другой,правый,проводник имеет NR проводящих подзон.Общее число каналов рассеяния равно Nr = NL+NR, поэтому матрица рассеяния есть Nr ×Nr унитарная матрица.Для удобства будем нумеровать каналы рассеяния так,что первые NL каналов рассеяния, 1 ≤ α ≤ NL, со - ответствуют левому контакту,а последние NR каналов рассеяния, NL + 1 ≤ α ≤ Nr, соответствуют правому контакту . Положим , что к левому резервуару приложен потенциал −V/2, а к правому резервуару приложен потенциал V/2. При этом следует учесть , что для всех подзон , принадлежащих какому либо одному проводнику,значения Vα совпадают,

Vα =	−V2 ,		1 ≤ α ≤ NL ,					(1.69)
		,	NL	≤	α	≤	Nr .
	V2

Ток,переносимый электронами в подзоне α, определяется выражением (1.53).Для упрощения вычислений мы рассмотрим случай нулевой те мпературы.Хотя вывод о четности кондактанса по магнитному пол ю остается справедливым и при конечных температурах.Итак,

41

1.Формализм Ландауэра-Бьюттикера

	Nr		>	?
	!
Iα = G0	|Sαβ|2		Vβ − Vα .		(1.70)
	β=1
			ˆ	вычисляются при E = µ0.
Здесь и ниже элементы матрицы рассеяния S
Для вычисления,например,тока IL, текущего в левом проводнике ,
необходимо сложить все токи,текущие в тех подзонах,которы					е соответ -
ствуют левому проводнику.Это подзоны с номерами от 1 до NL, поэтому ,
	NL
	!				(1.71)
	IL =	Iα .
	α=1
Подставляя выражение( 1.70) в выражение (1.71),получим,
	NL	Nr
	!	!
IL = V G0			|Sαβ|2 .		(1.72)

α=1 β=NL+1

Легко убедится с помощью аналогичных вычислений,что ток,т екущий в правый контакт ,IR = −IL, как и должно быть .

Отметим,что в выражение для тока IL/R входят только вероятности прохождения |Sαβ|2 между каналами рассеяния,принадлежащими различным проводникам.Другими словами,только процессы прохожд ение от одного электронного резервуара к другому электронному резервуару определяют величину протекающего тока.Ни процессы отражения в подзоне, ни процессы прохождения между подзонами одного проводника, что может рассматриваться как отражение в один и тот же резервуар,не в носят вклад в ток .

Рассмотрим кондактанс G = IL/V ,

NL	Nr
!	!
G = G0	|Sαβ|2 .	(1.73)

α=1 β=NL+1

Нашей задачей является показать,что эта величина четная по магнитному

42

1.4.Примеры

полю, G(H) = G(−H). Для этого введем коэффициенты отражения в ре - зервуары,

NL	NL	Nr	Nr
! !		!	!
RLL =	|Sαβ|2 , RRR =		|Sαβ |2 ,	(1.74)
α=1 β=1		α=NL+1 β=NL+1

и коэффициенты прохождения от одного резервуара в другой ,

		NL	Nr		Nr	NL
		! !			!	!
		TLR =	|Sαβ|2 ,		TRL =	|Sαβ|2 .	(1.75)
		α=1 β=NL+1			α=NL+1 β=1
Эти коэффициенты удовлетворяют следующим тождествам,
				" "	"	"
				NL NL	NL	Nr
		RLL + TLR =			|Sαβ|2 +	|Sαβ|2
			"	α=1 β=1	α=1 β=NL+1
				β"	"
			NL	Nr	NL
			=	|Sαβ|2 = 1 = NL ,
			α=1	=1	α=1	"
				" "	"
				NL NL	Nr	NL
		RLL + TRL =		α=1 β=1	|Sαβ|2 +	|Sαβ|2
					α=NL+1 β=1
			" "		β"
			NL	Nr	NL
			=	|Sαβ|2 = 1 = NL ,
			β=1 α=1		=1
							Nr
где мы использовали условия унитарности матрицы рассеяния,							=1 |Sαβ |2 =
	β"	|Sαβ|2 = 1. Из приведенных тождеств следует , что					α"
1,	Nr
	=1
				TLR = TRL .			(1.76)

43

1.Формализм Ландауэра-Бьюттикера

Далее,используя условие симметрии( 1.29) в магнитном поле для матрицы рассеяния,легко убедиться,что

TLR(−H) = TRL(H) .

(1.77)

Для доказательства последнего соотношения запишем,

"	"	"	"
NL	Nr	NL	Nr
TLR(−H) =		|Sαβ(−H)|2 =	|Sβα(H)|2
α=1 β=NL+1		α=1 β=NL+1

="Nr "NL |Sβα(H)|2 = TRL(H) .

β=NL+1 α=1

Таким образом,имеем

TLR = TRL					TLR(H) = TLR(	−	H),
TLR(	−	H) = TRL(H)

что,с учетом соотношения G = G0 TLR, доказывает четность по магнитному полю кондактанса образца с двумя квази-одномерными проводниками.

1.4.5.Ток,при наличии потенциального контакта

Покажем,что присоединение к мезоскопическому образцу доп олнительного контакта,например,для измерения электрическог о потенциала , существенно изменяет ток,протекающий через образец. [ 17] Физика рас - сматриваемого эффекта состоит в том,что наличие дополните льного контакта,соединенного с образцом в пределах области фазово-к огерентного рассеяния,влияет на вероятность рассеяния электронов меж ду контактами, используемыми для пропускания тока.Фактически,образец с двумя контактами и тот же самый образец с тремя контактами с точки зрения теории рассеяния-это различные образцы.

44

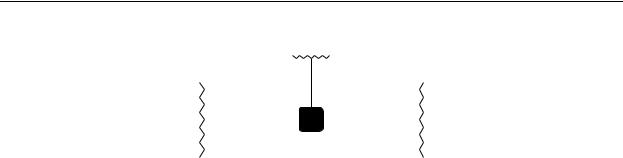
1.4.Примеры

µ3

I3 = 0

µ1 = µ0 + eV1				µ2 = µ0 + eV2

Рис. 1.6.Мезоскопический образец с потенциальным контактом.

Рассмотрим образец,соединенный с тремя различными контак тами, рис. 1.6. Два контакта , имеющие различные электрохимические потенциалы µ1 = µ0 + eV1 и µ2 = µ0 + eV2, используются для пропускания тока через образец.Третий контакт выполняет роль потенциально го щупа.Как и для всякого потенциального контакта , ток , текущий в этотонтакт равен нулю, I3 = 0. Это условие определяет электрохимический потенциал µ3 = µ0 + eV3 третьего резервуара как функцию приложенного между первым и вторым резервуарами напряжения, V = V2 − V1. Можно сказать , что V3 - это потенциал мезоскопического образца в той точке , к которой присоединен потенциальный контакт.

Вычислим ток,протекающий по образцу.Поскольку, I3 = 0, то I1 = −I2, как для образца , имеющего всего два контакта . Отсюда можнобыло бы предположить,что при заданном напряжении V величина тока определяется вероятностью рассеяния электрона из второго контакта в первый контакт.Однако это не так.При наличии потенциального контакт а,кондактанс, G12 = I1/V , зависит не только от вероятности рассеяния между токонесущими контактами,но и от вероятностей рассеяния между потен циальным и токонесущими контактами,

I1 =% G0T12V G12 %= G0T12 .

Из выражения( 1.53) следует ,

) *

I1 = G0 T12(V2 − V1) + T13(V3 − V1) ,

45

1.Формализм Ландауэра-Бьюттикера

) *

I2 = G0 T21(V1 − V2) + T23(V3 − V2) ,

) *

I3 = G0 T31(V1 − V3) + T32(V2 − V3) .

Из условия I3 = 0 определяем величину V3,

V3 = T31V1 + T32V2 .

T31 + T32

Отметим,что потенциал V3 = 0 в симметричном случае , а именно , когда V1 = −V2 и вероятность электрону перейти в третий резервуар из первого резервуара и из второго резервуара равны между собой, T31 = T32.

Используя полученное выражение для V3, найдем , что кондактанс ,

G12 = I1/(V2 − V1), равен ,

G12 = G0 6T12 +	T13T32	7 .
	T31 + T32

В том случае , если степень связи между потенциальным контактом и образцом мала, T31, T32 - T12, то мы возвращаемся к результату , полученному для образца с двумя контактами, G12 ≈ G0T12 .

1.4.6.Кольцо с рассеивателем

Приведенное ниже рассмотрение охватывает два общих случая, а именно: (i)кольцо с магнитным потоком Φ и (ii) кольцо с рассеивателем , у которого амплитуды прохождения в одном и в обратном направлениях различны.Для простоты мы полагаем,что рассеиватель,расп оложенный в точке x = 0, является точечным , то есть , его длинаw намного меньше длины окружности кольца L. Тогда мы можем выбрать волновую функцию электрона в кольце с магнитным потоком Φ, Рис .1.7, в следующем виде ,

x Φ
ψ(x) = +Aeik(x−L) + Be−ikx,ei2π L		, 0 ≤ x < L .	(1.78)
	Φ0

Рассеиватель описывается такой матрицей рассеяния:

46

1.4.Примеры

Aeiφ Ae−ikL

Be−ikLeiφ B

Φ

Рис. 1.7.Одномерное кольцо с рассеивателем.

-.

ˆ	S11	S12	.	(1.79)
S =	S21	S22

Тогда мы можем эффективно заменить рассеиватель следующими гранич - ными условиями для волновой функции( α = 1 для x → L − 0 и α = 2 для x → +0),

Be−ikLeiφ = AeiφS11 + BS12 ,

(1.80)

Ae−ikL = AeiφS21 + BS22 ,

где φ = 2πΦ/Φ0. Видно , что магнитный поток может быть устранен из урав - нений путем переопределения недиагональных элементов матрицы рассеяния,

S12) = S12 e−iφ , S21) = S21 eiφ .

(1.81)

Поэтому,далее мы не будем учитывать наличие магнитного пот ока,но при

47

1.Формализм Ландауэра-Бьюттикера

этом будем считать,что матрица рассеяния не симметрична пр и переста - новке индексов(в выражении( 1.79) следует сделать такие замены ,S12 →

S12) и S21 → S21) ).

1.4.6.1.Спектр

Сейчас мы вычислим одночастичный спектр электронов в кольце с еди - ничным рассеивателем.Дисперсионное уравнение,определя ющее допустимые значения импульса(волнового числа)электрона в кольце , получает - ся из условия совместности системы уравнений( 1.80).Мы перепишем эти уравнения следующим образом,

AS11 − B+e−ikL − S12) ,	=	0 ,	(1.82)
A+e−ikL − S21) , − BS22	=	0 .

Эти уравнения совместны,то есть имеют ненулевое решение от носительно неизвестных A и B, в том случае , когда определитель , составленный из коэффициентов при неизвестных обращается в нуль,

det ≡ +e−ikL − S21) ,+e−ikL − S12) , − S11S22 = 0 .

(1.83)

Для того,чтобы упростить решение этого уравнения мы сделае м такие за - мены,

S12) = te−iφ , S21) = teiφ .

(1.84)

Далее,мы разделим уравнение( 1.83) на S12) S21) = t2 и используем тожде - ство, S11S21) = −S12) S22, которое следует из условия унитарности для матри - цы рассеяния,и получим,

-	e−ikL	− eiφ.-	e−ikL	− e−iφ.		S22	2
					= −	|S21)	|2	.	(1.85)
	t		t
						|	|

48

1.4.Примеры

Обратим внимание на то,что амплитуда t может быть комплекснозначной. Поскольку правая часть уравнения( 1.85) является действительной , то и левая часть этого же уравнения должна быть действительной. Поэтому ,

выделяя действительную и мнимую части,получим следующие д ва уравнения,

:Re- −t

. − cos(φ);

+ sin2

(φ) − :Im-e−t

.;

= − T ,

(1.86a)

e ikL

2

ikL

2

R

Im-

e−ikL

.:Re-

e−ikL

. − cos(φ); = 0 .

(1.86b)

t

t

где |S22|2

= R ≥ 0 – коэффициент отражения, |S12)

|2 ≡ |t|2 = T ≥ 0

– коэффициент прохождения.Из уравнения( 1.86a)

мы заключаем , что

Im

e−ikL/t = 0. В противном случае знаки левой и правой частей это -

%

го

уравнения были бы различны.Далее из уравнения(

1.86b) мы получаем

+

,

дисперсионное уравнение,

Re-

e−ikL

. = cos(φ) ,

(1.87)

t

которое хорошо известно из литературы[ 18, 19].

Можно проверить непосредственным вычислением,что уравне ние (1.86a) совместно с уравнением (1.87).

1.4.6.2.Циркулирующий в кольце ток

Ток,переносимый электроном в состоянии с волновой функцие й (1.78) равен,

I =	e!k	A 2	− |B|2	.	(1.88)
	m
Обратим внимание на то,что магнитный+| |			поток Φ,	не входит в это выражение.

Поэтому,мы можем использовать это выражение независимо от того,есть

49

1.Формализм Ландауэра-Бьюттикера

ли магнитный поток в кольце или нет.В том числе это выражение может быть использовано для рассматриваемого нами случая,когда S12) %= S21) .

Для того,чтобы вычислить ток( 1.88),мы используем условие нормировки волновой функции,

L

ˆ

dx|ψ|2 ≡ |A|2 + |B|2 = 1 ,

(1.89)

0

и одно из уравнений системы (1.82),скажем,второе,

B = A

e−ikL − S21)

≡

A

e−ikL − teiφ

.

(1.90)

S22

S22

Подставляя выражения( 1.89) и (1.90) в (1.88) мы получим ,

| |

= T

@

e−ikL

@

2

,

F 2

eiφ

.

(1.91)

I = e!k 1 − |F |2

@

@

| |

@

−

@

mL 1 + F 2

R

t

Заметим,что при φ = 0, то есть , в симметричном@

случае@

S, 12)

= S21) , ток

Eq. (1.91) исчезает , поскольку|F |2 = 1. Последнее доказывается на ос -

новании уравнений( 1.86) и (1.87).Дисперсионное уравнение(

1.87) дает ,

Re

e−ikL/t

= 1. Тогда при φ = 0 мы получим из(

1.86a) следующее ,

A

+

e

ikL/t

,B

2

. Следовательно ,

2

A

+

ikL

,B

2

Im

= R/T

F

= T

Im e−

/t

/R =

+

−

,

|

|

T R/(T R) = 1.

Если рассеиватель не симметричный, S)

= S)

(то есть φ

= 0),

12

%

21

%

тогда ток отличен от нуля.Используя дисперсионное уравнен ие( 1.87),
Re	+e−ikL/t,		= cos(φ), мы вычислим |F |2:						.sin(φ) .
		T |F |2 = :Im -e−t			.;	+ sin2	(φ) − 2Im -e−t			(1.92)
		R		ikL		2		ikL

Затем из( 1.86) получим ,

50

1.4.Примеры

:Im- −t

.;

2

= sin2(φ) + T ,

e ikL

R

Подставляя это выражение вEq. ( 1.92) и затем в (1.91) найдем ток ,

I = −

e!k

T sin(φ)

.

(1.93)

mL

T sin(φ) +

R

sin(φ) − Im )e

−ikL

*

t

Если обозначить t = it0eiχ, тогда дисперсионное уравнение будет ,sin(kL +

χ) =n					этого уравнения как
	−t0 cos(φ). Запишем решениеiknL					/t	=		cos(k		knL + χ = πn +
( 1)	arcsin[t cos(φ)]. Тогда ,Im		+	e				−		L + χ)/t и ток (1.93)
равен−	,	0		−		,			n		0

In = − e!kn mL

			√				sin(φ)
					T				,	(1.94)
√			√					R
	T sin(φ) +

T sin(φ) + cos(knL + χ)

√

где T = t0.

В выражении для тока величина φ представляет собой или магнитный поток или характеризует асимметрию матрицы рассеяния, Eq. (1.84),обусловленную,например,внутренним магнитным моментом.В об щем случае величины R и T = 1 − R зависят от величины kn.

51